Represent Words as Vectors | TWO2TWO2TWO2TWO2

Why need word vectors?

To train a prediction model on a dataset of natural language, or corpus, one fundamental step is to extract features from it, mapping the textual data to real-valued vectors. These vectors contain properties of the linguistic items, which would be fed to our designed model as the input before we can start training. The quality of input vectors is vital to the performance of the model. If too much information of the corpus gets lost in the feature extraction step, the predictive performance of the model would be significantly reduced. Therefore, people make lots of effort to improve it. How to construct suitable embedding vectors has been a significant problem.

In earlier NLP researches, people did not tend to treat single words as atomic symbols because contexts affect the meaning of a word significantly. Take the word “bank” as an example. In the sentence, “People save money in a bank”, the word “bank” means a financial institution, while in the sentence “He sat on the bank of the river”, it means the land alongside a river. The exact meaning of a word can only be inferred from its nearby words, or from the document it appears in. Therefore, early methods embed the whole document as one vector, rather than regard words as separable components. The famous Bag of Words (BOW) method, represents a document as a vector $w\in\mathbb{R}^{|V|\times 1}$. In this notation, $|V|$ is the size of the vocabulary. For example, the sentence “The black cat loves the yellow cat.” can be expressed as:

$\begin{bmatrix}2&0&0&\cdots&2&1&\cdots&0\end{bmatrix}^T$

If the first word in the vocabulary is “the”, and the second is “a”, etc. The $i^{th}$ element $w_i$ denotes the number of times the $i^{th}$ word in the vocabulary appears in the document.

Although simple, BOW has been proven effective in some tasks, like document classification. BOW takes the advantage that similar types of documents use similar words. For example, the word “metaphysics” mostly appears in philosophy articles. However, BOW is unable to tell some more subtle differences. It does not consider the order of words, as well as the synonym. The BOW representations of the sentence “Alice loves Bob” and “Bob loves Alice” are the same, but their meanings are opposite.

When it comes to the era of deep learning, embedding language with word vectors begins to be widely accepted. This is due to the rapid development of word embedding approaches. Good word vectors have some beneficial properties. For example, vectors of similar words tend to be close to each other on some distance metrics. By representing sentences and documents as the sequences of word vectors, researchers achieve much better results than earlier methods. Due to its importance, most NLP beginners will get in touch with word embeddings in the first several lessons. In this article, four methods to generate word vector representations would be introduced. Though most times we do not need to train the word vectors by ourselves(it is very convenient to download pre-trained word vectors online), knowing about some details of how to train word vectors may help you design a better model. All these four methods were implemented and shared in my Github repository.

Generally speaking, there are two kinds of word vector methods, one is count-based, and the other is iteration-based. Most of the time, we prefer word vectors generated from iteration-based methods, but knowing about count-based methods would help you have a better understanding of some critical NLP concepts.

One-Hot Vector

This is the simplest method, which represents each word as a $\mathbb{R}^{|V|\times 1}$ vector with all 0s and only one 1 at the index of that word in the sorted English vocabulary. For example, the first word in the vocabulary, aardvark, would be represented as:

$w^{\text{aardvark}}=\begin{bmatrix}1&0&\cdots&0\end{bmatrix}^T$

Although simple and clear, the one-hot vector could not be used to capture the similarity of words directly because any two one-hot vectors are orthogonal, i.e., their inner product is always 0.

In fact, the BOW vector representation of a document is simply a sum of one-hot vectors of words in it.

$\text{BOW}(d)=\sum_i w_i^{one-hot}$

From this, we may find that BOW is problematic. As well, if the size of the vocabulary, $|V|$, grows too large, it would cost a considerable part of memory to store the vectors, which is an obstruct to training. Not only one-hot vector and BOW have this problem, but most count-based methods also suffer from it too. The most common way is to apply singular value decomposition (SVD) to reduce the vector dimensions. Given a matrix $\mathbf{M}$, SVD decomposes it by:

$\mathbf{M}=\mathbf{USV}^T$

where $\mathbf{S}$ is the singular value matrix, and $\mathbf{U}$ and $\mathbf{V}$ are two orthonormal matrices. After sorting singular values in $\mathbf{S}$ from big to small, the first $k$ columns of $\mathbf{U}$ would be taken as word vectors, where $k$ is the word vector dimension we desire.

code here

Co-Occurrence Matrix

To generate more useful word vectors than the one-hot vector, in most cases, we rely on the distributional hypothesis, set forth by Firth and Harris: the meaning of a word can be inferred from the contexts in which it is used. Similar words will be used in similar contexts. Therefore, we can extract features of words by discovering the contexts in which they occur. The context of a word could be several words co-occur with it, or the document it appears in. With this intuition in mind, many count-based methods were proposed.

Co-Occurrence matrix is one of the count-based methods. It counts the number of times every two words occur together in the corpus. Occurring together means one word appears in the context of the other word. We limit the context of a word to a window of fixed size $n$, which contains $n$ words before the word and $n$ words after the word, totally $2n$ words surrounding the target word. The co-occurrence matrix $\mathbf{M}$, in which $\mathbf{M}_{ij}$ is the number of times word $w_j$ appears inside the window of $w_i$. The $i^{th}$ row of the matrix is taken as the word vector of the word $w_i$. There is an example below, in which the corpus contains three sentences and the window size is 1:

I enjoy flying.
I like NLP.
I like deep learning.

The co-occurrence matrix is as follows:

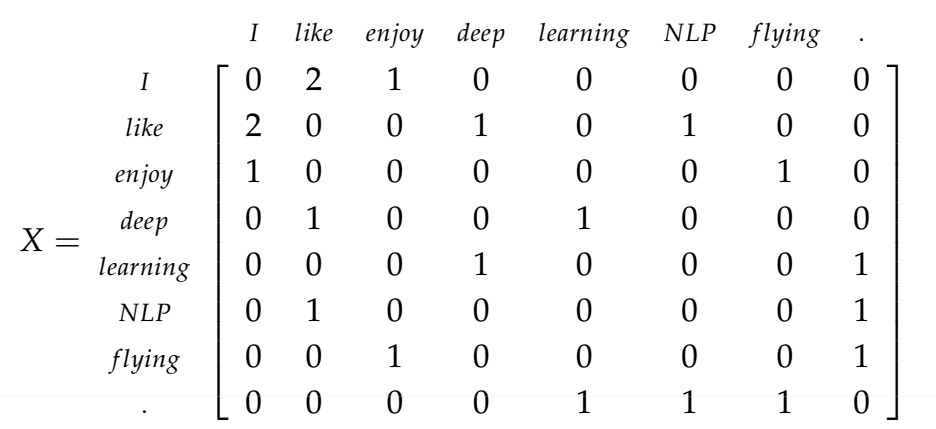
co-occurrence matrix

As we can see, the shape of the co-occurrence matrix is $|V|\times|V|$, and each word’s vector is $|V|\times 1$, same as the one-hot vector. This kind of vector can capture some extent of word similarity since words share a similar context if their vectors are similar. However, it is still a little naïve, and the dimension needs to be further reduced.

code here

Word-Context Matrix

Word-context matrix is another count-based method. It builds a word-context matrix $X$, in which $X{ij}$ is a value indicating the relevance between the word $w_i$ and the $j^{th}$ linguistic context (For example, a document. The linguistic context can even be single words. Defining the values to be the number of times that one word appears near the other word would result in a co-occurrence matrix). Denote the number of linguistic contexts as $|D|$, and then the shape of the word-context matrix would be $|V|\times|D$. Since similar words tend to appear in similar contexts, the word-context matrix can also capture the similarity between words. The $i^{th}$ word $w_i$ is represented by the $i^{th}$ row of the matrix. $X{ij}$ could be simply defined as the number of times that word $w_i$ appears in the context $c_j$. However, there would be a disadvantage that frequent contexts like “the cat”, “an apple”, receive higher scores than less frequent but more valuable contexts, like “cute cat”, “green apple”. Therefore, some would use the metric pointwise mutual information (PMI) to calculate $X{ij}$:

$\text{PMI}(w, c)=\log\frac{\#(w,c)\cdot|D|}{\#(w)\cdot\#(c)}$

PMI rescales matrix values by words’ marginal probabilities. Furthermore, the PMI value of word-context pair $(w,c)$ that were never observed in the corpus is $\log(0)=-\infty$. To avoid it, we modify PMI to be positive PMI (PPMI):

$\text{PPMI}(w,c)=\max(\text{PMI}(w,c),0)$

The co-occurrence matrix can also be improved with the PMI metric (rescaled by the words marginal probabilities). A common shortcoming of PMI and PPMI is that, if the context $c$ is rare in the corpus, the $\#(c)$ values would be small, which causes the PMI value very high. As a result, rare contexts usually have the largest PMI values, even though they may not be so semantically related to the word.

Although carefully defined, many count-based methods, including co-occurrence matrix and word-context matrix, have to face the problem that the matrix is sparse and high-dimensional. As well, when new words come into the corpus or the corpus is changed, it costs a lot to update the matrix, which would even change the shape of the matrix. That is why we need iteration-based methods, which could overcome these difficulties in an elegant way.

code here

Word2vec

Iteration-based methods try to create a model with an objective function and word vectors as parameters, quite like unsupervised machine learning tasks. At each iteration, the model updates parameters to optimize the objective. The optimization method might be Gradient Descent. The dimension of word vectors could be arbitrarily determined. Well-trained word vectors are dense and have ideal linguistic properties.

Word2vec is an epitome of iteration-based methods. Word2vec is a software package, including two algorithms: skip-gram and continuous bag-of-words (CBOW). These two algorithms are similar but based on different assumptions.

Skip-Gram

At each iteration, the skip-gram model selects a word $w_c$ as the center word, and $2m$ words in its window as the context words, where $m$ is the size of the window. Each word is assigned two vector representations: the center word representation $v$ (when it is a center word) and the context word representation $u$ (when it is a context word). The goal of the skip-gram model is to find word vectors that are useful to predict context words, or more formally, to maximize the posterior probability:

$P(u_{c-m}u_{c-m+1}\cdots u_{c-1}u_{c+1}\cdots u_{c+m}|v_{c})$

The skip-gram model assumes each context word is independent to each other:

$P(u_{c-m}u_{c-m+1}\cdots u_{c-1}u_{c+1}\cdots u_{c+m}|v_{c})=\prod_{-m\leq j\leq m,j\ne0}P(u_{c+j}|v_{c})$

The item $P(u_{o}|v_{c})$ is defined as a softmax function:

$P(u_{o}|v_{c})=\frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{|V|}\exp(u_w^Tv_c)}$

To maximize this probability is equivalent to minimize:

$-\sum_{-m\leq j\leq m,j\ne0}\log P(u_{c+j}|v_c)=\sum_{-m\leq j\leq m,j\ne0}\left(-u_{c+j}^Tv_c+\log(\sum_{w=1}^{|V|}\exp(u_w^Tv_c))\right)$

This is the objective function of the skip-gram model. Then for each $u$ and $v$, calculate their derivatives and update parameters to optimize the objective.

After finishing training, the center word representations are used as the word vectors, and the context representations are dropped.

Continuous Bag-of-Words

The CBOW model is similar to the skip-gram model, but instead of predicting surrounding words, the CBOW model predicts the center word given all context words. The CBOW also assigns two word vectors to each word: $u$ (when it is a center word) and $v$ (when it is a context word). The goal of CBOW model is to maximize:

$P(u_c|v_{c-m},v_{c-m+1},\cdots,v_{c-1},v_{c+1},\cdots,v_{c+m})$

$v_{c-m},v_{c-m+1},\cdots,v_{c-1},v_{c+1},\cdots,v_{c+m}$ can be replaced by their average:

$\hat{v}=\frac{1}{2m}\sum_{-m\leq j\leq m,j\ne0}v_{c+j}$

Then, the objective can be written as:

$\begin{align}-\log P(u_c|\hat{v})&=-\log\frac{\exp(u_c^T\hat{v})}{\sum_{w=1}^{|V|}\exp(u_w^T\hat{v})}\\ &=-u_c^T\hat{v}+\log\sum_{w=1}^{|V|}\exp(u_w^T\hat{v})\end{align}$

Parameters are updated to optimize the objective at each iteration, just like what we do in the skip-gram model.

Negative Sampling

Each time we evaluate the objective function of word2vec, we must go through the whole vocabulary, and the time complexity would be $O(|V|)$, which is not computationally efficient. To alleviate this, (take the skip-gram as an example), we only sample several negative samples for each center-context word pair. These negative samples are sampled from a noise distribution $P(w)$, whose probabilities match the ordering of the frequency of the vocabulary. In practice, we set

$P(w) =C(w)^{3/4}/Z$

where $C(w)$ is the count of word $w$ in the corpus, and $Z$ is the normalization term. Raising the frequency to the $\frac{3}{4}$ power is to increase the probability of rare words. This definition of $P(w)$ works best in practical training.

In a negative sampling skip-gram model, the goal is to distinguish true context words against negative sampling words. We use the sigmoid function to define the probability:

$P(u_o|v_c)=\frac{1}{1+\exp(-u_o^Tv_c)}$

and the object becomes to maximize:

$P(u_o|v_c)\prod_{k\sim P(w)}(1-P(u_k|v_c))$

which is equivalent to minimize:

$\begin{array}-\log P(u_o|v_c)-\sum_{k\sim P(w)}\log(1-P(u_k|v_c))\\=-\log\frac{1}{1+\exp(-u_o^Tv_c)}-\sum_{k\sim P(w)}\log\frac{1}{1+\exp(u_k^Tv_c)}\end{array}$

Similar to the skip-gram, for CBOW, the negative sampling objective function is:

$-\log\frac{1}{1+\exp(-u_c^T\hat{v})}-\sum_{k\sim P(w)}\log\frac{1}{1+\exp(u_k^T\hat{v})}$

Suppose at each iteration, $k$ negative samples are generated (for small datasets, a $k$ between 5 to 20 is appropriate). As a result, the time complexity of each iteration would be reduced to $O(k)$, which is significantly less than $O(|V|)$. The performance of the softmax and negative samples are comparable, but the negative samples is much more efficient.

code here

Word2vec Summary

There are many pre-trained word vectors to download and use from the Internet. You can choose the one you like and explore it. For example, you can use APIs from Python libraries:

import gensim.downloader as api
wv_from_bin = api.load("word2vec-google-news-300")

This block of code will load the word vectors set pre-trained with the Google News corpus. The dimension of the word vectors is 300 and the vocabulary size is about 3 million. You might be surprised if you do this kind of vector addition and subtraction on downloaded word vectors:

# precompute L2-normalized vectors
wv_from_bin.init_sims()
# linear combination & normalization
king = wv_from_bin.word_vec('king', use_norm=True)
man = wv_from_bin.word_vec('man', use_norm=True)
woman = wv_from_bin.word_vec('woman', use_norm=True)
target = (king + woman - man)
target /= np.linalg.norm(target)
# find the most similar vectors (cosine similarity)
dists = np.dot(wv_from_bin.vectors_norm, target)
best = np.argsort(dists)[-1:-11:-1]
for idx in best:
    word = wv_from_bin.index2word[idx]
    if word not in ['king', 'man', 'woman']:
        print('word: {:<20}distance: {:<20}'.format(word, dists[idx]))

# ================= output =================
# word: queen               distance: 0.7118192911148071  
# word: monarch             distance: 0.6189674139022827  
# word: princess            distance: 0.5902431011199951  
# word: crown_prince        distance: 0.5499460697174072  
# word: prince              distance: 0.5377321243286133  
# word: kings               distance: 0.5236844420433044  
# word: Queen_Consort       distance: 0.5235945582389832  
# word: queens              distance: 0.518113374710083   
# word: sultan              distance: 0.5098593235015869

We can see that the word vector of “queen” is at the top of the result list! This is an exciting property of word2vec, proving its powerful ability to capture word similarity. Due to its impressive performance, word2vec has become one of the most popular word embedding methods.

However, is that iteration-based methods necessarily outperform count-based methods since they have so many advantages? The answer might be no. Iteration-based methods fail to capture valuable information too. Actually, word2vec is based on windows, which poorly utilizes the statistics of the whole corpus but focuses only on local contexts. The GloVe model tried to retrieve more global information by combining traditional and iterative methods. The GloVe makes use of the co-occurrence matrix to capture similarities between words. However, in the paper of Omer Levy, the author pointed out that by effectively tuning hyperparameters, the performance of count-based and iteration-based models would be largely comparable. This means that there is still no mature method, which could outperform all other methods.

Reference

Neural Network Methods for Natural Language Processing. Yoav Goldberg.
Distributed Representations of Words and Phrases and their Compositionality. Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, and Jeffrey Dean.
GloVe: Global Vectors for Word Representation. Jeffrey Pennington, Richard Socher, Christopher D. Manning.
Improving Distributional Similarity with Lessons Learned from Word Embeddings. Omer Levy, Yoav Goldberg, Ido Dagan
CS224n
Dive into Deep Learning

Hope you can give me some advice by connecting me two2er2@gmail.com if I made some mistakes.

Why need word vectors?

One-Hot Vector

Co-Occurrence Matrix

Word-Context Matrix

Word2vec

Skip-Gram

Continuous Bag-of-Words

Negative Sampling

Word2vec Summary

Reference

Share on: