Neural Machine Translation in Seq2eq

This is a learning note of studying CS224N. Seq2seq is a beautiful recurrent neural network (RNN) variant, whose inputs and outputs both are sequences. Its applications include machine translation, speech recognition, text summarization, and conversational models, etc. Seq2seq is a broad field to explore, and researches related are still active. This post only discusses the fundamental part of seq2seq and introduces its application on machine translation, which was proposed together with the model in its original paper.

Seq2seq

The encoder-decoder structure was firstly proposed by Cho (2014). This model consists of two RNNs, in which one is the encoder, and the other is the decoder. The encoder receives a variable-length sequence input, encoding it to be a vector $c$, which could be regarded as a summary of the sequence. Then, the decoder would predict the target sequence words conditioned on this summary $c$ (you can think it as the context) and previously predicted sequence words.

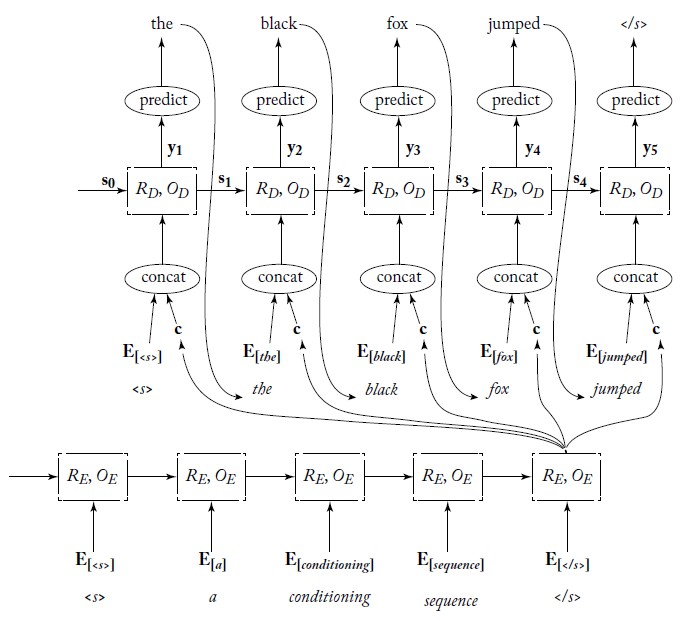
encoder_decoder

Note that during training, at the $t^{th}$ time step, the decoder predicts the target sequence words conditioned on $c$ and the $t^{th}$ word in the gold-standard target sentence rather than the last prediction. The loss function could be softmax cross-entropy loss, and the encoder and decoder are trained together.

The seq2seq is based on the encoder-decoder structure. In a seq2seq model, the last hidden state is used to initialize the decoder’s first hidden state, passing information from the input sequence to the decoder. In the original paper, some tricks improving the performance of the model were introduced. They are:

Reverse the order of words in the input sentence to introduce more short term dependencies. Intuitively, doing this would make the last word of the input sequence “close” to the begin of the target sentence, and easier for the decoder to “get started” on the output.
Use multi-layer LSTM, which significantly outperforms single layer LSTM and simple RNN. LSTM is generally better than simple RNN on capturing long term dependencies, and it is easier to train.

Besides these tricks, as described in the CS224N course notes, the seq2seq could be improved by adding other features. One of the most useful ideas is the Attention mechanisms. The last hidden state of the encoder might miss sequential information since it compresses the sequence. As the length of the input sequence increases, the last hidden state would be less capable of summarizing the sequence. Concerning this issue, Attention is proven to be a smart solution. In a decoder augmented by the Attention, the context vector is no longer the last hidden state of the encoder, but a weighted sum of all hidden states produced by the encoder. At each time step, the weight of the$i^{th}$ hidden state of the encoder is determined by the current hidden state of the decoder with itself. Since the weights for every hidden state are different, the context seems to pay “attention” in some words, which might be more related to the current word in the target sequence. This is an idea to “align” the input and the target sequences. More details would be shown below. Attention could be “local” as well. Local Attention focuses on a window of encoder hidden states but not all hidden states. By constraining the size of the window, the computational cost of the attention step would be constant.

Another great idea is the Beam Search. Beam search is not a new technique. As described before, the decoder predicts the word at the $t^{th}$ time step conditioned on predictions from $1$ to $t-1$ time steps, which is more a greedy strategy and may not result in the global optimized output. Therefore, at each time step, we can maintain $K$ candidates rather than keep only one prediction. These candidates, or hypotheses, could be denoted as the following:

$\mathcal{H}_t=\{(x_1^1,\cdots,x_t^1),\cdots,(x_1^K,\cdots,x_t^K)\}$

where $x_i^j$ is the $i$-th word in the sequence of the $j$-th candidate. They are the most possible prediction sequences till the current time step. At the next time step, these candidates are extended by appending words to their sequences:

$\mathcal{H}^\tilde{k}_{t+1}=\{(x_1^k,\cdots,x_t^k,v_1),\cdots,(x_1^k,\cdots,x_t^k,v_{|V|})\}$

where $|V|$ is the size of the vocabulary. Then, the new $K$ candidates are selected from

$\tilde{\mathcal{H}}_{t+1}=\bigcup_{k=1}^K\mathcal{H}^\tilde{k}_{t+1}$

by their joint probabilities. Beam search is a trade-off between greedy search and exhaustive search. It is more likely to find an optimal target sequence than greedy search while maintaining good computational efficiency.

Model Details

This part would describe some implementation details of the seq2seq model following the CS224N course note. This implementation not necessarily outperforms others. It is just an example to help understand the seq2seq model. Any hyperparameters and networks could be changed since this is not the only standard.

Firstly, the encoder is a bidirectional LSTM which summarizes the input sequence. Since the encoder is bidirectional, reversing the input sequence does not help. Therefore, the sequence is fed to the encoder in the original order. The states of the forward and backward LSTM are concatenated to give the hidden states $\mathbf{h}_i^{enc}$ and cell states $\mathbf{c}_i^{enc}$ of the encoder:

$\begin{aligned} \mathbf{h}_i^{enc}=[\overleftarrow{\mathbf{h}_i^{enc}};\overrightarrow{\mathbf{h}_i^{enc}}]\ &\text{where}\ \mathbf{h}_i^{enc}\in\mathbb{R}^{2h\times1},\overleftarrow{\mathbf{h}_i^{enc}},\overrightarrow{\mathbf{h}_i^{enc}}\in\mathbb{R}^{h\times1}\\ \mathbf{c}_i^{enc}=[\overleftarrow{\mathbf{c}_i^{enc}};\overrightarrow{\mathbf{c}_i^{enc}}]\ &\text{where}\ \mathbf{c}_i^{enc}\in\mathbb{R}^{2h\times1},\overleftarrow{\mathbf{c}_i^{enc}},\overrightarrow{\mathbf{c}_i^{enc}}\in\mathbb{R}^{h\times1} \end{aligned}$

where $h$ is the hidden size, $\overleftarrow{\mathbf{h}_i^{enc}},\overrightarrow{\mathbf{h}_i^{enc}},\overleftarrow{\mathbf{c}_i^{enc}},\overrightarrow{\mathbf{c}_i^{enc}}$ are hidden states and cell states of the forward and backward LSTM.

These states extract features of the sequence, which are components of the context vector for the decoder. With context information ready, we turn to the decoder. The decoder is a unidirectional LSTM. Its first hidden state $\mathbf{h}_0^{dec}$ and cell state $\mathbf{c}_0^{dec}$ are initialized with a linear projection of the encoder’s final states:

$\begin{aligned} \mathbf{h}_0^{dec}=\mathbf{W}_h[\overleftarrow{\mathbf{h}_1^{enc}};\overrightarrow{\mathbf{h}_m^{enc}}]\ &\text{where}\ \mathbf{h}_0^{dec}\in\mathbb{R}^{h\times1},\mathbf{W}_h\in\mathbb{R}^{h\times2h}\\ \mathbf{c}_0^{dec}=\mathbf{W}_c[\overleftarrow{\mathbf{c}_1^{enc}};\overrightarrow{\mathbf{c}_m^{enc}}]\ &\text{where}\ \mathbf{c}_0^{dec}\in\mathbb{R}^{h\times1},\mathbf{W}_c\in\mathbb{R}^{h\times2h} \end{aligned}$

where $m$ is the length of the input sequence. After initializing, we feed an item to the decoder at each time step. On the $t^{th}$ time step, we concatenate the embedding vector of the last predicted word (or the current gold-standard target word) with the combined-output vector from the previous timestep (it could be thought as a combination of the context vector from the encoder and the previous hidden state of the decoder, which contains both context and sequential information. The first combined-output vector $\mathbf{o}_0$ is a zero-vector):

$\overline{\mathbf{y}_t}=[\mathbf{y}_t;\mathbf{o}_{t-1}], \text{where}\ \overline{\mathbf{y}_t}\in\mathbf{R}^{(e+h)\times1},\mathbf{y}_t\in\mathbf{R}^{e\times1},\mathbf{o}_{t-1}\in\mathbb{R}^{h\times1}$

This $\overline{\mathbf{y}_t}$ would be fed to the decoder LSTM.

$\mathbf{h}_t^{dec},\mathbf{c}_t^{dec}=\text{Decoder}(\overline{\mathbf{y}_t},\mathbf{h}_{t-1}^{dec},\mathbf{h}_{t-1}^{dec})\ \text{where}\ \mathbf{h}_t^{dec},\mathbf{c}_t^{dec}\in\mathbb{R}^{h\times1}$

To compute $\mathbf{o}_{t-1}$, we must know the context vector $\mathbf{a}_{t-1}$. In this version of seq2seq, the context vector is the output of an attention step. The $i^{th}$ hidden state of the encoder is assigned a weight $\alpha_{t-1,i}$ to reflect its relevance to the previous hidden state $\mathbf{h}_{t-1}^{dec}$ of the decoder:

$\begin{aligned} \mathbf{e}_{t-1,i}=(\mathbf{h}_{t-1}^{dec})^T\mathbf{W}_{attProj}\mathbf{h}_{i}^{enc}\ &\text{where}\ \mathbf{e}_{t-1,i}\in\mathbb{R}^{m\times1},\mathbf{W}_{attProj}\in\mathbb{R}^{h\times2h}\\ \alpha_{t-1}=\text{Softmax}(\mathbf{e}_{t-1})\ &\text{where}\ \alpha_{t-1}\in\mathbb{R}^{m\times1}\\ \mathbf{a}_{t-1}=\sum_{i}^{m}\alpha_{t-1,i}\mathbf{h}_i^{enc}\ &\text{where}\ \mathbf{a}_{t-1}\in\mathbb{R}^{2h\times1} \end{aligned}$

The context vector $\mathbf{a}_{t-1}$ is a weighted sum of hidden states of the encoder, which outperforms the last hidden state of the encoder as the context. Then, $\mathbf{a}_{t-1}$ and the previous hidden state $\mathbf{h}_{t-1}^{dec}$ are concatenated and passed through a linear layer with activation function to attain the combined-output vector $\mathbf{o}_{t-1}$:

$\begin{aligned} \mathbf{u}_{t-1}=[\mathbf{a}_{t-1};\mathbf{h}_{t-1}^{dec}]\ &\text{where}\ \mathbf{u}_{t-1}\in\mathbb{R}^{3h\times1}\\ \mathbf{v}_{t-1}=\mathbf{W}_u\mathbf{u}_{t-1}\ &\text{where}\ \mathbf{v}_{t-1}\in\mathbb{R}^{h\times1},\mathbf{W}_{u}\in\mathbb{R}^{h\times3h}\\ \mathbf{o}_{t-1}=\text{Dropout}(\text{Tanh}(\mathbf{v}_{t-1}))\ &\text{where}\ \mathbf{o}_{t-1}\in\mathbb{R}^{h\times1} \end{aligned}$

The combined-output not only acts as the input of the next time step but also summarizes information for predicting the target. It is passed to a softmax layer to produce the probability distribution $\mathbf{P}_t$ over the target word:

$\mathbf{P}_t=\text{Softmax}(\mathbf{W}_{vocab}\mathbf{o}_t)\ \text{where}\ \mathbf{P}_t\in\mathbf{R}^{|V|\times1},\mathbf{W}_{vocab}\in\mathbf{R}^{|V|\times h}$

where $|V|$ is the size of the vocabulary. In the training process, $\mathbf{P}_t$ would be compared with the one-hot vector $\mathbf{g}_t$ of the expected target word, to compute loss (softmax cross-entropy loss by default):

$J_t=CE(\mathbf{P}_t,\mathbf{g}_t)$

Note that the encoder and the decoder are trained together on this loss. In the seq2seq described in my post (and as well, the CS224N course note), the context vectors are derived from the attention mechanism. It performs well compared with only using the last hidden state $\mathbf{h}_m^{enc}$ of the encoder as the context. However, it also has some problems. If the input sequence is too long, the computational cost of the attention step would be unaffordable. To alleviate this issue, you may try to limit the attention field to a window, or other variants of the vanilla attention.

Conclusion

Encoder-decoder is the core structure of many neural models in NLP. Since firstly proposed in 2014, it has had plenty of applications and a profound impact on its field. It is still under exploration and development because it is a relatively new concept. From my perspective, the most significant breakthrough of the encoder-decoder (seq2seq) is that it divides the model into two parts: the encoder and the decoder. These two RNNs could process variable-length sequences while remaining well alignment between the input and the target sequences. The encoder-decoder also inspires practical ideas like Attention, which comes from encoder-decoder but has broader applications.

Reference

Sequence to Sequence Learning with Neural Networks. Ilya Sutskever, Oriol Vinyals, Quoc V. Le.
Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. Kyunghyun Cho, Bart van Merrienboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, Yoshua Bengio.
Neural Network Methods for Natural Language Processing. Yoav Goldberg.
Neural Machine Translation by Jointly Learning to Align and Translate. Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio.
Effective Approaches to Attention-based Neural Machine Translation. Thang Luong, Hieu Pham, Christopher D. Manning.
CS224N
Dive into Deep Learning

Seq2seq

Model Details

Conclusion

Reference

Share on: