Recently I read a paper called Fast k-Nearest Neighbour Search via Dynamic Continuous Indexing [1] and its 2.0 version Fast k-Nearest Neighbour Search via Prioritized DCI [2]. Since this is one of the research topics of my MSc. Dissertation, I would like to make some comments on it. In my opinion, the two methods, DCI and pDCI, proposed by the same author Ke Li, have a strong relation to LSH [3]. LSH is a big family of hash-based kNN algorithms. To illustrate my view, I choose the Random Projection implementation, which was described in [4]. The pseudo-code of this implementation is as following:
Algorithm 1 LSH Random Projection
-----------------------------------------------
Require: A dataset D of n points p[1], p[2], ..., p[n], the number of random vectors m that constitute a (composite) projection and the number of projections L, the number of bins on each vector
function CONSTRUCT(D, m, L)
u[m][L] <- m*L random unit vectors in R^d
for i = 1 to n do
for l = 1 to L do
for j = 1 to m do
compute the inner product between random vector u[l][j] and p[i]
according to the product, put p[i] into one of bins of u[l][j]
end for
end for
end for
end function
function QUERY(q, k):
C[L] <- L arrays of size n with entries initialized to 0
S[L] <- L empty sets
for l = 1 to L do
for j = 1 to m do
compute the inner product between random vector u[l][j] and q
according to the product, put q into one of bins of u[l][j]
for all samples i in that bin do
C[L][i] <- C[L][i] + 1
if C[L][i] = m then
S[l] <- S[l] UNION {i}
end if
end for
end for
end for
return k points in the union of S[l] ∀l∈L that are the closest in Euclidean distance in R^d to q
end function
This is not the original procedure of the Random Projection LSH implementation described in [4], but a modification to follow the variables naming and writing style of Ke Li. Some steps seem unnecessary, like adding candidates into S[L] according to the current (composite) projection rather than adding them into a big set S. This is deliberate for comparison with DCI/pDCI, and it will not affect anything except for a little bit computation cost.
The reason why we need m random vectors (in [4], the author used the notation k to denote the number of random vectors) and L composite projections was clearly explained in [4]. In [1], the idea of setting L composite indices with m simple indices each is quite similar to the idea of the composite projection, and I believe that Ke Li was inspired by LSH to some extent when he invented DCI though he did not talk about this in his paper.
For a clear comparison, the pseudo-code of DCI would also be placed here, as follows:
Algorithm 2 Dynamic Continuous Indexing (DCI)
-----------------------------------------------
Require: A dataset D of n points p[1], p[2], ..., p[n], the number of random vectors m that constitute a (composite) projection and the number of projections L, the number of bins on each vector
function CONSTRUCT(D, m, L)
u[m][L] <- m*L random unit vectors in R^d
T[m][L] <- m*L empty binary search trees
for i = 1 to n do
for l = 1 to L do
for j = 1 to m do
compute the project of p[i] on u[l][j]
according to the project, insert p[i] into T[l][j]
end for
end for
end for
end function
function QUERY(q, k):
C[L] <- L arrays of size n with entries initialized to 0
S[L] <- L empty sets
for i = 1 to n do
for l = 1 to L do
for j = 1 to m do
compute the project of q on u[l][j]
pi <- the sample in T[j][l] whose key is i-th closest to the project of q
C[L][i] <- C[L][i] + 1
if C[L][i] = m then
S[l] <- S[l] UNION {i}
end if
end for
end for
if IsStoppingConditionSatisfied() then
break
end if
end for
return k points in the union of S[l] ∀l∈L that are the closest in Euclidean distance in R^d to q
end function
As we can see, the layout of the code is quite similar to that of LSH. Actually, the effect of projecting points onto random indices is equivalent to that of calculating the inner products of points with random vectors. The reason is that by projecting points on a line, we evaluate the distance between them only on one dimension. That means for every point we can keep only a scalar (e.g., the value of the first dimension) to memory its position on the line and evaluate the distance. On the other hand, the inner products of points with a random vector is also a scalar. Since the indices and vectors are randomly generated, the scalars they produced have no difference.
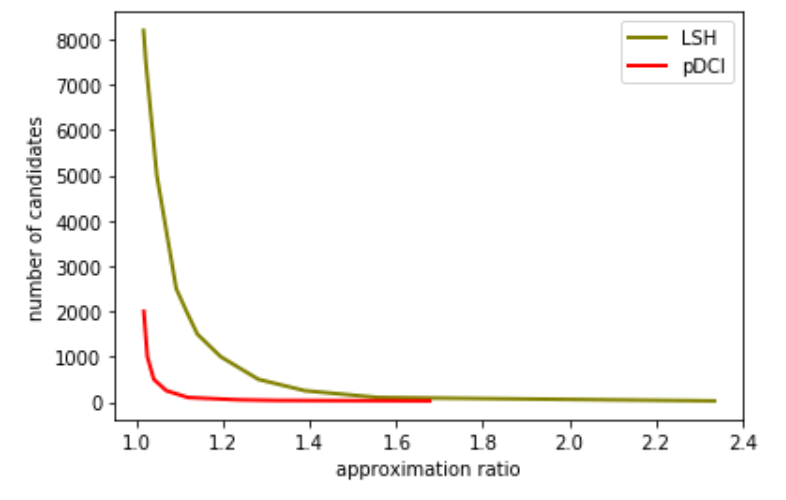
The Random Projection LSH uses the hash binning strategy of directly partitioning the 1-dimensional projection space into several bins. The DCI uses a more sophisticated and implicit binning strategy, in which the width of bins is dynamic. The DCI iterates sample points in the order of their distances to the query point and ends when a certain condition is satisfied. Suppose the number of average points to be visited is x. The distance of the x-th sample with the query point is the width of the bins on that index. This width could be adapted to the density of the dataset, while the width of LSH is fixed and performs worse when the dataset is sparse or distributed non-uniformly. However, though DCI shows improvement in the binning strategy, it still follows the basic idea of LSH, and that is why I think DCI is just a variant of LSH. It is intuitive that DCI could have a much small size of the set of candidate points (i.e., the S), because it has a more advanced selecting strategy. The experiment figures plotted in the original papers of DCI/pDCI are curved on the number of candidates (b.t.w., Ke Li said the number of distance evaluations (i.e., candidates) could be used as an implementation-independent proxy for the query time, which is strongly suspected by myself), showing that DCI indeed has a much smaller size of candidates set.
The pDCI is the improved version of DCI. For each composite index, pDCI considers the projection closest to the query point first, no matter which simple index it belongs to. More concretely, pDCI uses L priority queues. For each composite index, pDCI pushes all projections on the m simple indices into the corresponding queue with their distances to the query point projection as the keys. Sample points are visited in the order of their places in the queues, rather than by iteration. Intuitively, pDCI gives priority to those sample points that are more likely to be in the k nearest neighbors. If a sample is far away from the query point on one of the simple indices, its projection on this index would have a low priority in its queue, resulting in that this point is less likely to be visited m times before the algorithm terminates and be selected as a candidate. This could be regarded as another improvement of the binning strategy, but as it does not escape from the basic idea, pDCI is still one kind of LSH. In my opinion, DCI/pDCI is a variant of Random Projection LSH with a sophisticated binning strategy, which reduces the number of candidates largely. The implicit problem of DCI/pDCI is that it spends much more time filtering out candidates. As we can see, during the construction of indices, DCI/pDCI needs projects n samples onto the m*L indices, which means n*m*L times of d-dimensional projections would be taken. If the number of query points is less than m*L, it would be a loss trading since the naive linear search method needs fewer times of Euclidean distance calculations. As I noticed, the m and L must be large enough to guarantee the querying accuracy. The setting of these two hyper-parameters is highly related to the number of samples n and the dimension d. When n and d is high, simple indices would be very diverse, i.e., they disagree with each other on which sample point is the closest to the query point. These simple indices are just like weak learners in the machine-learning ensemble model. The number of weak learners must be higher than a threshold to have acceptable accuracy. Therefore, the number of query points should be high enough, otherwise applying DCI/pDCI to do kNN search is meaningless.
To reproduce the experiment result shown in [2], and remeasure the wall-clock time of pDCI, I design a simple experiment. The number of query points should be much larger than 100, which is the test number in [2].
In this experiment, the dataset is MNIST, and the setting of hyper-parameters (m and L) follows the settings in the original paper, which is m = 15, L = 3. Empirically, these numeric values are too small to have good accuracy while k0 and k1 are set followed the formulas on the paper. However, since the author did not mention his setting of k0 and k1, I would set both of them as +INF, and use the number of selected candidates nc as the condition of termination. nc is a good hyper-parameter to balance the accuracy and query time. As well, if an algorithm could select candidates efficiently, even nc is equal to k, the accuracy would be very high. On the other hand, if the algorithm has a low ability to filter out candidates, it must have a much bigger nc to guarantee that the k nearest neighbors are in the set of candidates. Therefore, by altering nc, we can control the accuracy of the algorithm output. By setting nc small, we can also shorten the query time (especially the process of filtering out candidates). In my opinion, nc is a much better hyper-parameter for users than k0 and k1. k0 and k1 are hard to tune. They are related to m, L, n, d, which are too implicit for users. Even users set k0 and k1 just a little smaller than the intrinsic threshold, pDCI might not be able to filter out any candidates and result in an empty return set.
The experiment is taken on my own machine, which has an AMD Ryzen 2700x CPU and 32GB memory. Due to the limit of computation resources, I used only 10000 random sampled samples from the whole dataset. I use K-fold cross-validation to evaluate with K=10. Therefore, the size of the samples is 9000, and the number of query points is 1000.
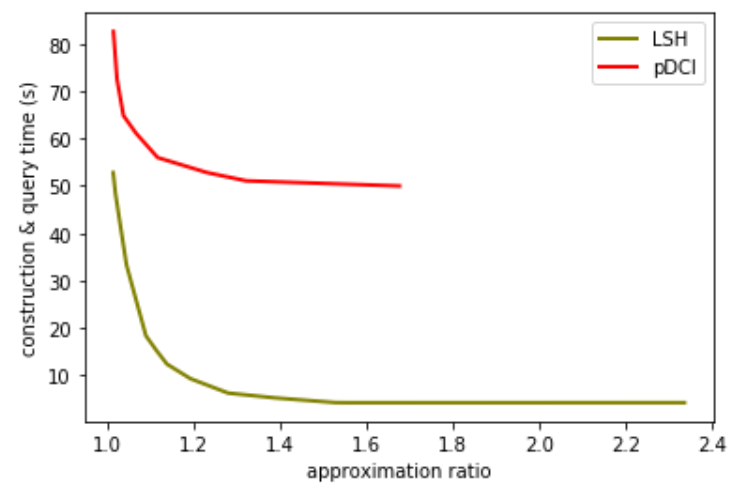
The experiment result is consistent with the figure 2 in the paper. However, this result is not surprising. pDCI spends much more time filtering out candidates, and that it has a better candidate set is reasonable. Figure 2 only shows that the quality of candidates of pDCI is better. As to efficiency, we must consider the real spent time (construction time + query time). Since the processes of construction are essentially the same, the difference in total time is determined only by the query time. The construction time is about 2.2s, and query time dominates in my experiment.
[1] Li, Ke, and Jitendra Malik. “Fast k-nearest neighbour search via dynamic continuous indexing.” In International Conference on Machine Learning, pp. 671-679. 2016.
[2] Li, Ke, and Jitendra Malik. “Fast k-nearest neighbour search via prioritized dci.” In Proceedings of the 34th International Conference on Machine Learning-Volume 70, pp. 2081-2090. JMLR. org, 2017.
[3] Datar, Mayur, Nicole Immorlica, Piotr Indyk, and Vahab S. Mirrokni. “Locality-sensitive hashing scheme based on p-stable distributions.” In Proceedings of the twentieth annual symposium on Computational geometry, pp. 253-262. 2004.
[4] M. Slaney and M. Casey, “Locality-Sensitive Hashing for Finding Nearest Neighbors [Lecture Notes],” in IEEE Signal Processing Magazine, vol. 25, no. 2, pp. 128-131, March 2008.