搜索树
搜索树是一种非常常见的数据结构。搜索树的节点对象包含key和value两个成员变量。给定一棵搜索树和一个指定key,我们可以通过在这棵树种找到具有对应key的节点,取得其value,来完成一次key->value的映射操作。这个想法是C++map数据结构的根本,C++ map就是用红黑树搜索树实现的。当然,C++的unordered_map使用哈希函数作为映射方法,增删改查的效率都和以搜索树为基础的映射方法不同。由于搜索树概念的重要性,它在面试中常考,“手写红黑树”已经成为面试者口口相传的一个恐怖传说……
下面是(二叉)树节点和树基类的代码实现。下文的一些搜索树继承自该基类。
template <typename T, typename U>
struct TreeNode {
T key;
U value;
int height;
TreeNode *left, *right, *parent;
TreeNode(T key, U value, int height = -1, TreeNode *parent = nullptr,
TreeNode *left = nullptr, TreeNode *right = nullptr)
: key(key), value(value), height(height),
parent(parent), left(left), right(right) {}
};
template <typename T, typename U>
class SearchTree {
protected:
TreeNode<T, U> *root;
public:
SearchTree() : root(nullptr) {}
~SearchTree() {
_delete(root);
}
void _delete(TreeNode<T, U> *node) {
if (!node) return;
_delete(node->left), _delete(node->right);
delete node;
}
#define getHeight(node) ( (node) ? (node)->height : -1 )
void updateHeight(TreeNode<T, U> *node) {
int Lheight = getHeight(node->left), Rheight = getHeight(node->right);
node->height = 1 + (Lheight > Rheight ? Lheight : Rheight);
}
};
二叉搜索树
最基本的搜索树是二叉搜索树(Binary Search Tree,BST)。它具有以下性质:
任一节点r的左(右)子树中,所有节点的key值(若存在)均不大于(不小于)r。
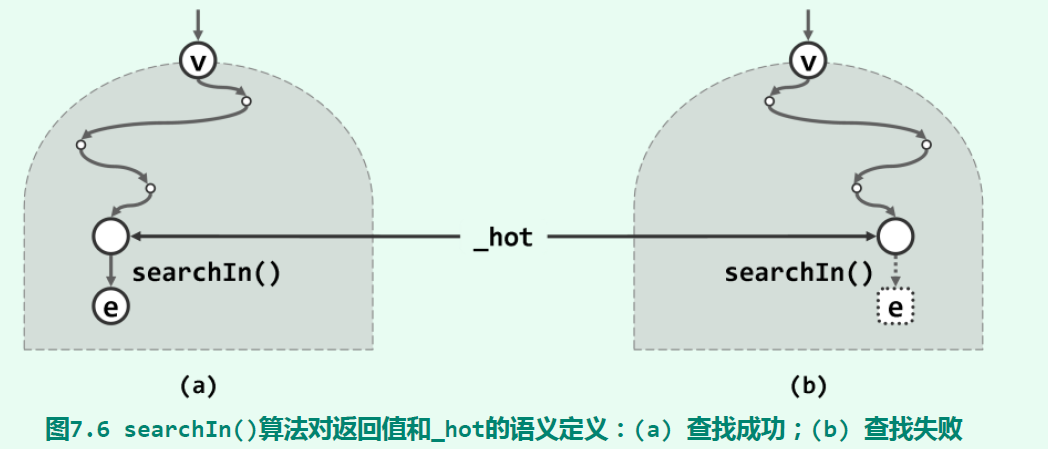
对二叉搜索树进行中序遍历,遍历序列肯定是单调非降的,这个很容易证明。为了简便讨论,假设二叉树的节点没有重复的key值。在二叉搜索树上进行查找,思路也非常简单:对于当前节点,如果它的key值和给定key值一样,那么返回该节点的value值;如果小于当前节点key值,则进入其左孩子继续查找;否则进入其右孩子继续查找。下面代码中,返回搜索结果节点的引用。如果在二叉搜索树中没有key值为key的节点,则返回一个空节点的引用。另外,参考《数据结构(C++语言版)》(丁俊晖,第三版),在搜索过程中更新_hot节点,表示当前到达节点的父节点。无论是查找成功还是查找失败,_hot都是一个有效节点。如下图,可以认为查找失败时,返回了一个所谓的“哨兵节点”。
可以看到,二叉搜索树的搜索时间复杂度和结果节点所在的层数有关。层数在1到n(节点数)间变动。如果树是一个完全二叉树,层数至多为O(logn),搜索效率较为理想。因此,提高二叉搜素树搜索效率的一种手段就是让树更平衡,也就是形似完全二叉树。平衡二叉搜索树(Balanced Binary Search Tree,BBST)有多种,包括AVL树、伸展树、红黑树等,区别在于平衡的方法。在提及平衡二叉搜索树之前,先了解二叉搜索树插入、删除节点的方法。
在一棵二叉搜索树种插入一个给定key value的节点,只需要对key值进行搜索。如果二叉搜索树中早已存在该key值,我们直接忽略这次操作,因为假定了树节点没有重复值。如果树中不存在该key值,返回的是一个空节点引用。可以证明,这个空节点所在位置,就是新节点的一个合理插入位置。因为利用它的key值一路搜索行成的搜索路径,是满足二叉搜索树定义的。此时_hot是它的父节点。不过,由于我们的search函数返回的是节点引用,直接修改节点值即可,无需为_hot添加左孩子或右孩子。
对二叉搜索树节点的删除比较麻烦。如果要删除的节点m是一个叶子节点那还好办,直接将m置为空;如果m上有老下有小,那么需要在它的孩子中挑选出一个节点来代替它。显然,如果它只有一个孩子,那么让那个孩子来代替它就行了,满足二叉搜索树定义;如果它有两个孩子,那么可以找出它左子树中最大的节点,或者右子树中最小的节点n来代替它。为了方便,我们使用n。这里替代的做法是交换m和n的数据,然后删除n。n显然最多只有一个孩子(而且只能是右孩子),删除它很容易,只要让它的父节点指向n的右孩子即可。
从代码中可以看到,插入、删除节点的时间复杂度和树的高度依然息息相关。为了提高查找、插入、删除的效率,优化树的高度是很有必要的。
template <typename T, typename U>
class BinarySearchTree : public SearchTree<T, U> {
protected:
using SearchTree<T, U>::root;
TreeNode<T, U> *_hot; // parent of the current returned node
TreeNode<T, U>*& _search(TreeNode<T, U> *&node, T key) {
if (!node || node->key == key) return node;
_hot = node;
return _search(node->key > key ? node->left : node->right, key);
}
void _remove(TreeNode<T, U> *&node) {
TreeNode<T, U> *obj = node; // node to remove
// only one child
if (!node->left) node = node->right;
else if (!node->right) node = node->left;
else { // has both children
// find succeed node
TreeNode<T, U> *succ = node->right, *parent = node;
while (succ->left) parent = succ, succ = succ->left;
// swap data
node->key = succ->key, node->value = succ->value;
// delete succeed node
if (parent == node) parent->right = succ->right;
else parent->left = succ->right;
obj = succ;
}
delete obj;
}
public:
BinarySearchTree() : SearchTree<T, U>() {}
TreeNode<T, U>*& search(T key) {
_hot = nullptr;
return _search(root, key);
}
void insert(T key, U value) {
TreeNode<T, U>* &node = search(key);
if (node) return; // key already in tree
// don't care heights and parents
node = new TreeNode<T, U>(key, value);
}
void remove(T key) {
TreeNode<T, U>* &node = search(key);
if (!node) return; // no such node
_remove(node);
}
};
AVL树
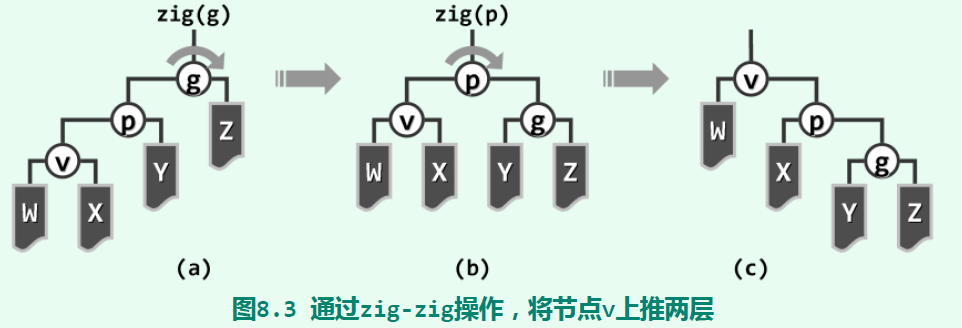
AVL树(AVL tree)是最早被发明的平衡二叉搜索树,其中的AVL来源于发明者的姓名。在渐进意义下,AVL数可始终将树高度控制在O(logn)以内,从而保证查找、插入、删除操作的时间复杂度也为O(logn)。AVL树有一套“平衡”的标准:任一节点都有一个平衡因子(balance factor),定义为其左右子树的高度差。在本文中,空树的高度为-1,单节点树的高度为0。所谓AVL树,即平衡因子受限的二叉搜索树,其每个节点平衡因子的绝对值均不超过1。可以想象,一棵AVL树具有类似完全二叉树的姿态。它的子树也是AVL树,形如一个锥形。在插入删除节点后,如果打破了AVL树原有的平衡,会对某个子树进行不超过两次的旋转操作,使其恢复平衡。旋转操作有以下两种,分别是zig和zag:
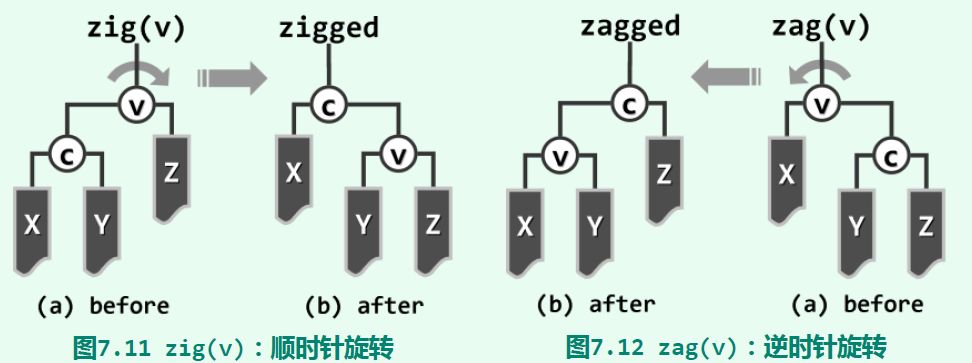
zig zag操作虽然简单,但它们能保证旋转后的二叉搜索树是等价变换的,即中序遍历序列相等。zig zag旋转后,原二叉搜索树的性质不会改变。显然,插入节点x的父节点不可能失衡,但是父节点高度可能会加一,导致x的祖父节点可能会失衡。因此,那些因插入x的节点,最深的不深过x的祖父节点。记这个最深的平衡因子绝对值不小于1的节点为g,在g通往x的路上,依次经过的前三个节点为g->p->v。g p v可能的场景有四种:
g->right == p, p->right == vg->right == p, p->left == vg->left == p, p->left == vg->left == p, p->right == v
显然,第3、4种是第1、2种的镜面对称,我们只需讨论如何处理第1、2种场景即可。对于第一种场景,旋转操作如下:
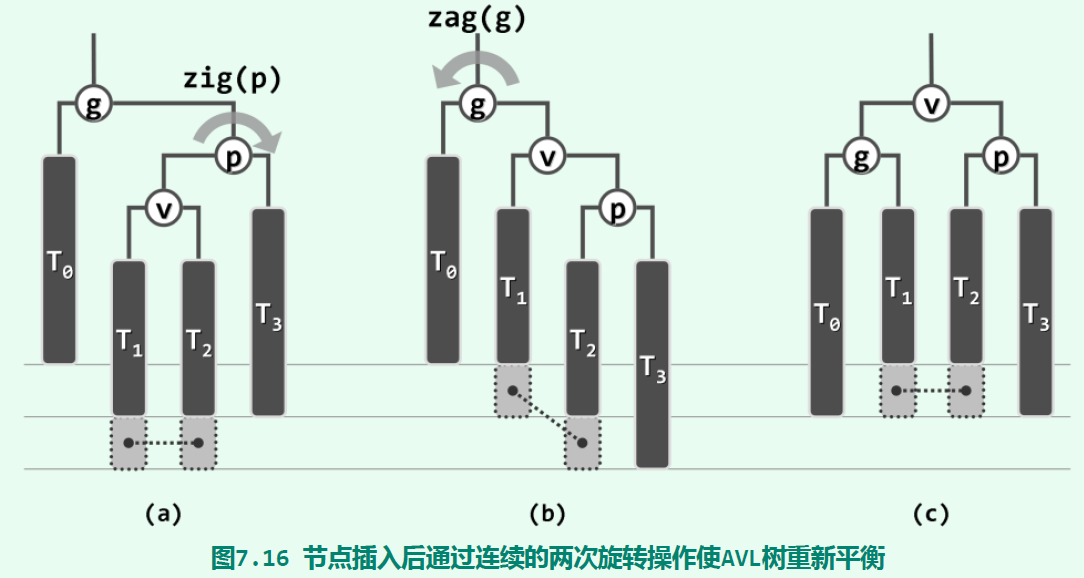
第二种场景需要一次zig操作加一次zag操作,才能让AVL树恢复平衡。对于第3、4种场景,只需要镜面对称操作即可。
如果是因为删除节点导致的失衡,处理方式会稍微不同。删除的节点可能是叶子节点,也可能是一个至多仅有右孩子的中间节点。因此后果仅是可能让包含这个节点的子树高度减一。可以证明,因此导致的失衡节点(平衡因子绝对值超过1)至多只有1个。同时,这个失衡节点g可能是被删除节点x的父节点。在确定了g的位置后,在它不包含x的一侧,必有一个非空孩子p(因为这一侧比另一侧高2单位导致了失衡),且p也必有孩子(至少一个)。从p的孩子中选出更高者v;如果等高则优先选和p同向者(即,v与p同为左孩子或右孩子)。下图示意g->left == p, p->left == v、x属于T3的场景,通过一次zig操作即可使AVL树重新平衡:
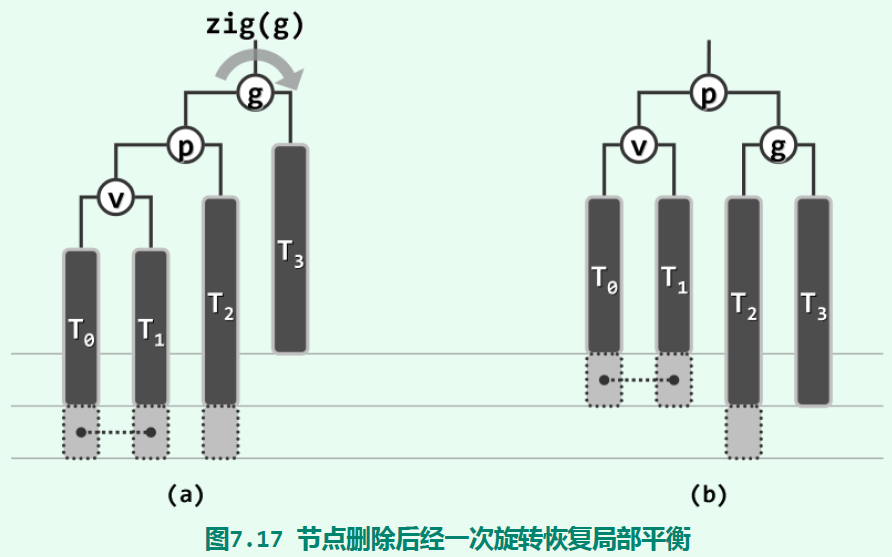
图中连接的灰色方框表示不会同时为空的两个节点;另一个灰色方框表示可有可无的节点。另一种场景g->left == p, p->right == v、x属于T3如下:
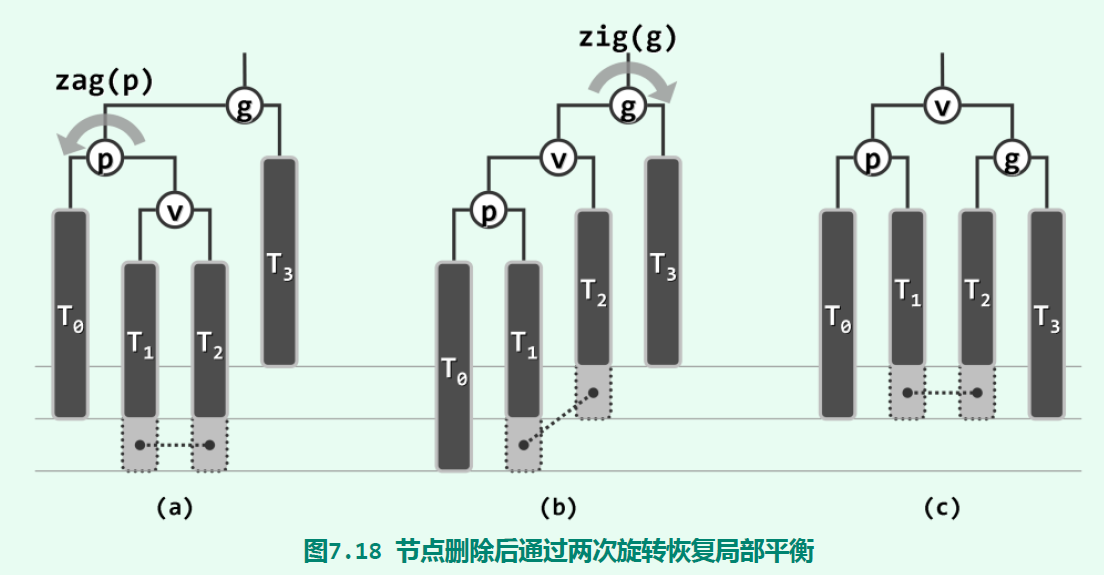
在至多两次旋转操作后也恢复了平衡。然而,这棵以g为根的子树虽然恢复平衡了,但它的高度可能会减1,导致它的祖先节点继续失衡!因此,在平衡该子树后,还要继续向上检查节点,是否保持平衡;对于失衡的节点要再进行旋转操作。
从上面4张图中,我们可以总结出它们的模式:在恢复平衡后,它们都展现出一种“3+4”结构:
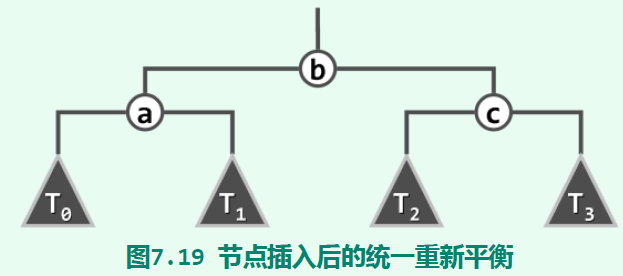
其中,a b c是g p v的某一个。我们可以通过识别旋转前a b c的相对位置,来确定旋转后它们应该在的位置。因此,我们只需要在旋转前的子树上提取出a b c T0 T1 T2 T3,然后组装成“3+4”结构,就能完全重新平衡操作,无须真的去旋转。这种思路能让代码变得异常简洁。
template <typename T, typename U>
class AVLTree : public BinarySearchTree<T, U> {
protected:
using SearchTree<T, U>::root;
using BinarySearchTree<T, U>::_hot;
using SearchTree<T, U>::updateHeight;
using BinarySearchTree<T, U>::_remove;
#define balanceFactor(node) ( getHeight((node)->left) - getHeight((node)->right) )
#define isLChild(node) ( (node)->parent && (node)->parent->left == (node) )
#define fromParentTo(node) \
((node)->parent \
? (isLChild(node) ? (node)->parent->left : (node)->parent->right) \
: root)
bool AvlUnbalanced(TreeNode<T, U> *node) {
int bf = balanceFactor(node);
return -1 > bf || bf > 1;
}
TreeNode<T, U> *tallerChild(TreeNode<T, U> *node) {
// return the taller child. if left.height == right.height, return the
// one of same side
int Lheight = getHeight(node->left), Rheight = getHeight(node->right);
if (Lheight > Rheight) return node->left;
else if (Rheight > Lheight) return node->right;
else if (isLChild(node)) return node->left;
else return node->right;
}
TreeNode<T, U>* rotate(TreeNode<T, U> *v) {
TreeNode<T, U> *p = v->parent, *g = p->parent;
// connect 3+4 structure based on relation between g, p, v
if (isLChild(p)) { // zig
if (isLChild(v)) { // zig-zig
p->parent = g->parent;
return connect34(v, p, g, v->left, v->right, p->right, g->right);
} else { // zig-zag
v->parent = g->parent;
return connect34(p, v, g, p->left, v->left, v->right, g->right);
}
} else { // zag
if (isLChild(v)) { // zag-zig
v->parent = g->parent;
return connect34(g, v, p, g->left, v->left, v->right, p->right);
} else { // zag-zag
p->parent = g->parent;
return connect34(g, p, v, g->left, p->left, v->left, v->right);
}
}
}
TreeNode<T, U>* connect34(TreeNode<T, U> *a, TreeNode<T, U> *b, TreeNode<T, U> *c,
TreeNode<T, U> *T0, TreeNode<T, U> *T1, TreeNode<T, U> *T2, TreeNode<T, U> *T3) {
a->left = T0; if (T0) T0->parent = a;
a->right = T1; if (T1) T1->parent = a; updateHeight(a);
c->left = T2; if (T2) T2->parent = c;
c->right = T3; if (T3) T3->parent = c; updateHeight(c);
b->left = a; a->parent = b;
b->right = c; c->parent = b; updateHeight(b);
return b;
}
public:
using BinarySearchTree<T, U>::search;
AVLTree() : BinarySearchTree<T, U>() {}
void insert(T key, U value) {
TreeNode<T, U>* &node = search(key);
if (node) return; // key already in tree
// height = 0, parent = _hot
node = new TreeNode<T, U>(key, value, 0, _hot);
// update heights & check balance factors for ancestors
for (TreeNode<T, U> *g = _hot; g; g = g->parent) {
if (AvlUnbalanced(g)) { // rotate based on g, p, v
TreeNode<T, U>* &parent = fromParentTo(g);
parent = rotate(tallerChild(tallerChild(g)));
break;
} else { // insert node increases heights of ancestors
updateHeight(g);
}
}
}
void remove(T key) {
TreeNode<T, U>* &node = search(key);
if (!node) return; // no such node
_remove(node);
// update heights & check balance factors for ancestors
for (TreeNode<T, U> *g = _hot; g; g = g->parent) {
if (AvlUnbalanced(g)) { // rotate & get root of the subtree
TreeNode<T, U>* &parent = fromParentTo(g);
g = parent = rotate(tallerChild(tallerChild(g)));
}
updateHeight(g);
}
}
};
伸展树
伸展树(splay tree)是平衡二叉搜索树的另一种形式。相比AVL树,伸展树无须时刻都严格保持全树的平衡,但却能够在任何足够长的真实操作序列中,保持分摊意义上的高效率。伸展树的核心思路是局部性。对于二叉搜索树,数据局部性具体体现在:
- 刚刚被访问过的节点,极有可能在不久以后再次被访问到
- 将被访问的下一节点,极有可能就处于不久之前被访问过的某个节点的附近
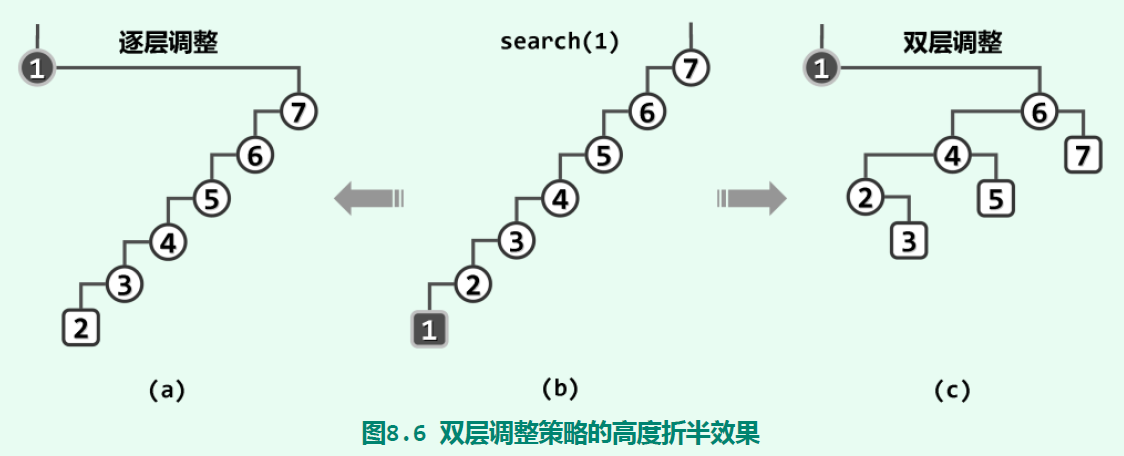
因此,只需将刚被访问的节点,及时转移到树根(附近),即可加速后续的操作。最直接的一种转移方法是逐层伸展,即不断旋转它的父节点,每次让它向上移动一层:
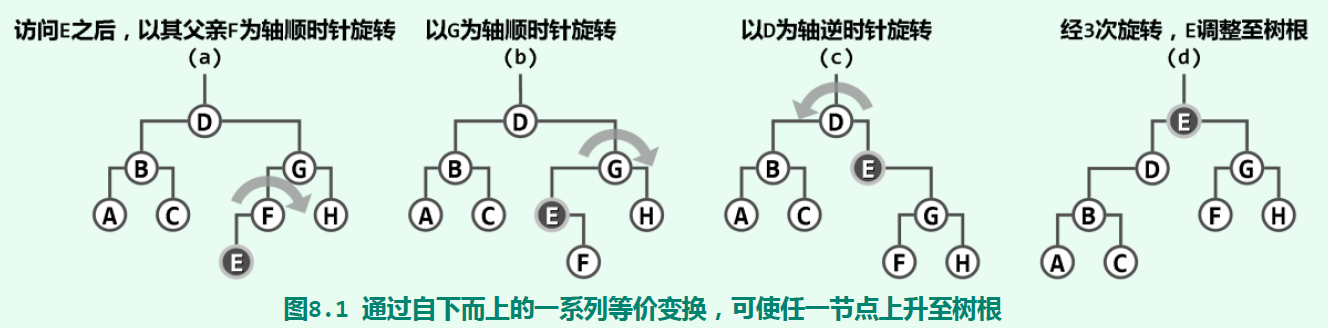
这种伸展方法并不好,在极端情况下,它的单次访问分摊时间复杂度可能为O(n)(参考《数据结构(C++语言版)》(丁俊晖,第三版) P205页的例子)。一种较好的伸展方式是双层伸展,即每次都从当前节点v向上追溯两层,并根据其父节点p以及祖父节点g的相对位置,进行相应的旋转。旋转方式有zig和zag,经过至多两次旋转,就能将v转移到以g为根的子树的根节点处。双层伸展的移动轨迹和逐层伸展很相似,但是它有zig-zig或zag-zag这种操作:
就是说,它会先把v上面的节点先旋转了,然后再将v向上提。每次将v向上移动两层,当v离根节点只有一层时,再通过一次zig或zag旋转,即可将它转移到整棵树的根节点处。可以证明,在进行双层伸展将节点转移到根处后,树的结构会比逐层伸展调整得更加平衡。就树的形态而言,双层伸展策略能“折叠”被访问的子树分支,从而有效地避免对长分支的连续访问。可以证明,双层伸展的伸展树的单次操作可在分摊的O(logn)时间内完成。
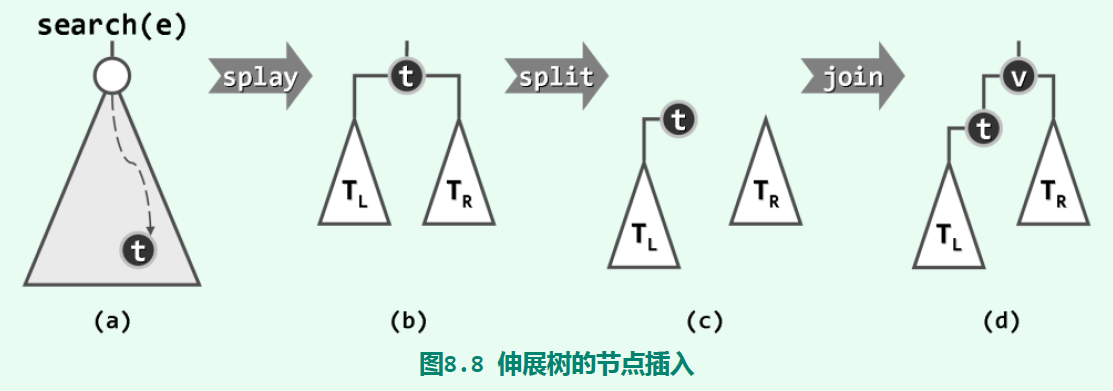
伸展树的查找、插入、删除操作基于二叉搜索树,只是加上了伸展的操作。在查找到节点后,需要将其转移到根节点处。插入之前,会先查找插入位置,将插入位置的父节点提到根节点处。然后,根据插入节点和根节点的值大小关系,将插入节点插入到根节点的位置:
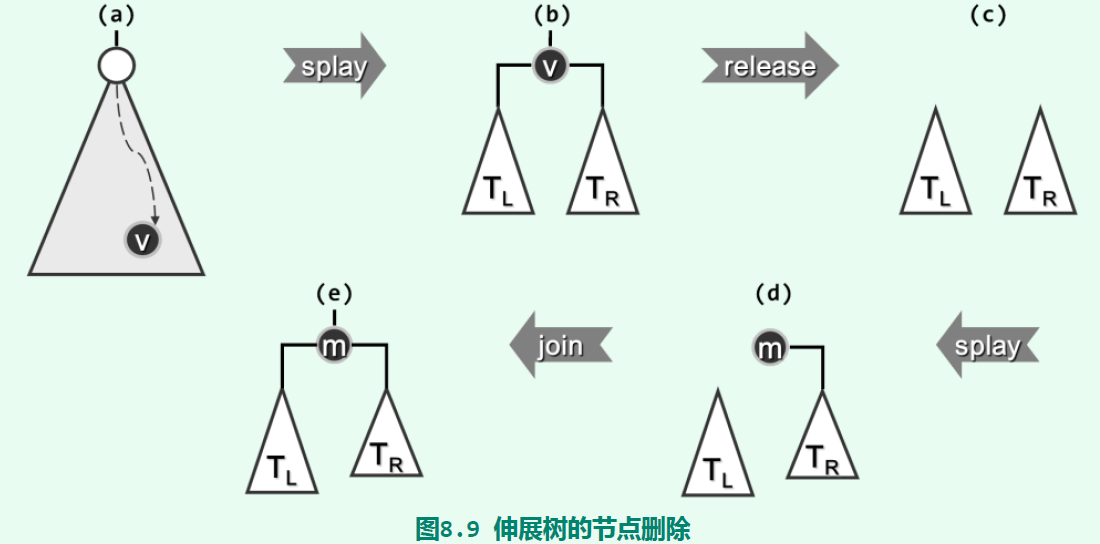
删除操作和插入操作类似;在搜索到删除节点后,删除节点会被提升到根节点处,然后将其删除。这样,伸展树就变成了两棵子树。然后,我们可以以删除的key值再搜索一次右子树。由于右子树上所有的键值都会大于key,所以这次搜索后,_hot是右子树中键值最小的节点。将其提升到右子树根节点处,它不可能有左孩子。因此,只需要将左子树设为该节点的左孩子即可。其实,也可以在左子树中搜索key,这样根节点处是比key小的最大节点。
template <typename T, typename U>
class SplayTree : public BinarySearchTree<T, U> {
protected:
using SearchTree<T, U>::root;
using BinarySearchTree<T, U>::_hot;
using BinarySearchTree<T, U>::_remove;
using BinarySearchTree<T, U>::_search;
void attachAsLChild(TreeNode<T, U> *node, TreeNode<T, U> *lc) {
node->left = lc; if (lc) lc->parent = node;
}
void attachAsRChild(TreeNode<T, U> *node, TreeNode<T, U> *rc) {
node->right = rc; if (rc) rc->parent = node;
}
TreeNode<T, U>* splay(TreeNode<T, U> *v) {
// move the node to root
if (!v) return nullptr;
TreeNode<T, U> *p, *g, *gg;
while ((p = v->parent) && (g = p->parent)) {
gg = g->parent; // parent of the subtree
if (isLChild(v)) {
if (isLChild(p)) { // zig-zig
attachAsLChild(g, p->right); attachAsLChild(p, v->right);
attachAsRChild(p, g); attachAsRChild(v, p);
} else { // zig-zag
attachAsLChild(p, v->right); attachAsRChild(g, v->left);
attachAsLChild(v, g); attachAsRChild(v, p);
}
} else if (!isLChild(p)) { // zag-zag
attachAsRChild(g, p->left); attachAsRChild(p, v->left);
attachAsLChild(p, g); attachAsLChild(v, p);
} else { // zag-zig
attachAsRChild(p, v->left); attachAsLChild(g, v->right);
attachAsRChild(v, g); attachAsLChild(v, p);
}
if (!gg) { // v is root now
v->parent = nullptr;
} else {
(g == gg->left) ? attachAsLChild(gg, v) : attachAsRChild(gg, v);
}
}
if (p = v->parent) { // g is null, need one more zig/zag
if (isLChild(v)) { // zig
attachAsLChild(p, v->right); attachAsRChild(v, p);
} else { // zag
attachAsRChild(p, v->left); attachAsLChild(v, p);
}
}
v->parent = nullptr; // set as root
return v;
}
public:
TreeNode<T, U> *&search(T key) {
_hot = nullptr;
TreeNode<T, U> *v = _search(root, key);
root = splay((v ? v : _hot)); // set the last visited node as root
return root;
}
void insert(T key, U value) {
if (!root) { root = new TreeNode<T, U>(key, value); return; }
TreeNode<T, U>* node = search(key);
if (key == node->key) return; // key already in tree
root = new TreeNode<T, U>(key, value);
node->parent = root;
if (node->key < key) {
root->left = node; root->right = node->right;
if (node->right) {
node->right->parent = root; node->right = nullptr;
}
} else {
root->right = node; root->left = node->left;
if (node->left) {
node->left->parent = root; node->left = nullptr;
}
}
}
void remove(T key) {
if (!root || search(key)->key != key) return; // no such node
TreeNode<T, U> *to_delete = root;
if (!root->left) { // delete root directly
root = root->right;
if (root) root->parent = nullptr;
} else if (!root->right) {
root = root->left;
if (root) root->parent = nullptr;
} else {
root = root->right; root->parent = nullptr;
search(key); // search right subtree
root->left = to_delete->left; to_delete->left->parent = root;
}
delete(to_delete);
}
};
B-树
B-树(B-tree)利用了计算机系统中另一个重要概念——分级存储,在存储数据量巨大的前提下,无法将所有数据都放在内存中,因此要尽量减少外存访问次数,以增加内存访问次数折中。为了达到这个目的,B-树,或者更广泛的多路搜索树(multi-way search tree),将节点和它的孩子合并为一个“大节点”:
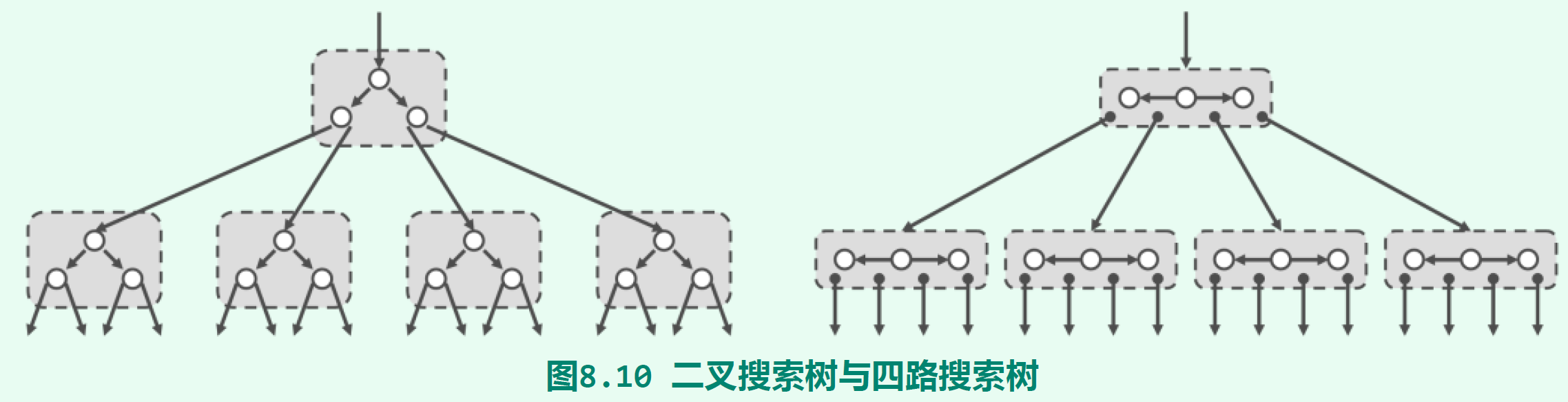
合并后的“大节点”具有若干个key值,原本单个节点的二叉路径被收拢在一起,形成了多叉节点。如上图右,将节点和它的左右孩子合并,左右孩子的孩子成为大节点的孩子,使得树变成一棵四叉树,称为四路搜索树。一般来说,将k层节点合并,可以得到一棵2^k路搜索树。多路搜索树相比二叉搜索树的优势是,在读取外存的节点时,能够一次将节点中的key值读入,而非像二叉搜索树每次读入一个key值。由于同一个大节点中的key值在逻辑上与物理上都彼此相邻,所以批量从外存读入所需的时间与读取单个key值得时间几乎一样。每个节点保存的最佳key值数目和不同外存的批量访问特性有关。
所谓m阶B-树,即m路平衡搜索树(m>2),它处于最底层的节点输入外部节点,其他节点属于内部节点:
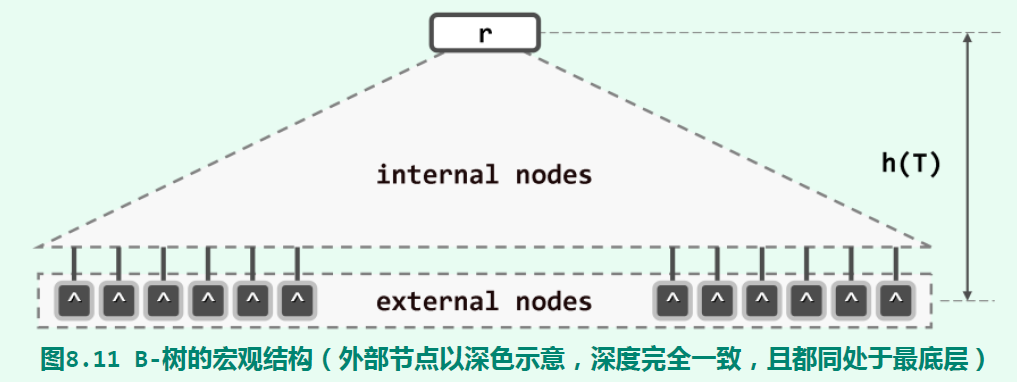
其中,所有外部节点的深度都相等(都在最底层)。同时,每个内部节点都存有不超过m-1个key值,以及用于指示对应分支的min(ceil(m/2), 2) <= x <= m个引用(即孩子,根节点例外。一般来说key值数为分支数减一)。因此,m阶B-树也称为(ceil(m/2), m)-树。一般来说,大数据集会以B-树形式放置于外存中。对于活跃的B-树,其根节点会常驻于内存;此外,任何时刻通常只有另一个节点(称为当前节点)留驻于内存。在搜索时,将需要的节点载入内存,顺序扫描其包含的key值匹配搜索值(由于数量不大,不必使用二分查找),通过分支指示进入孩子节点。m阶B-树的查找、插入、删除操作的时间复杂度都为O(log_m(N))。
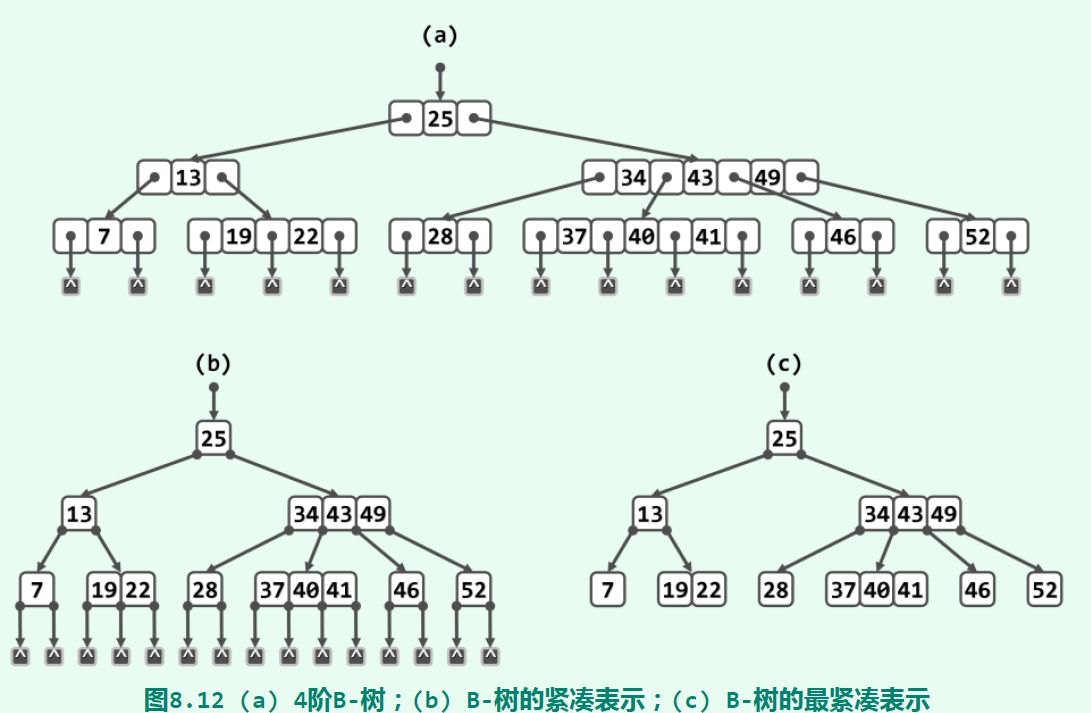
在代码实现上,由于B-树的节点可以有多个key值,所以不能再用二叉数的节点类了。这里选择用vector来装key,value,以及孩子。在插入、删除操作中,由于为节点增加、删除一个key值,可能导致节点的key值数量不合法(数量上溢(overflow)或下溢(underflow)),需要触发分裂(split)和合并(merge)的操作来处理。
在插入一个key值后,如果节点的key值数量为m,那么会触发分裂操作。具体地说,将其第floor(m/2)个(从0开始数)上移到它的父节点中,然后其左边的key值划分为一个节点,右边的key值划分为一个节点;两个节点作为原本父节点的孩子存在。如果分裂的操作导致父节点也发生上溢,会继续分裂父节点。
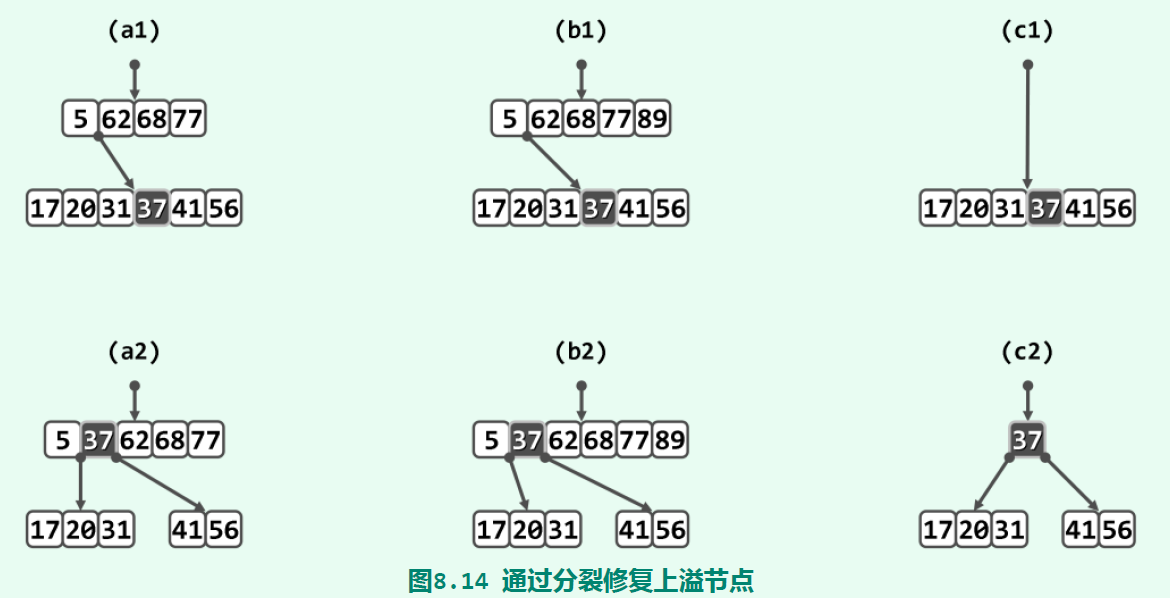
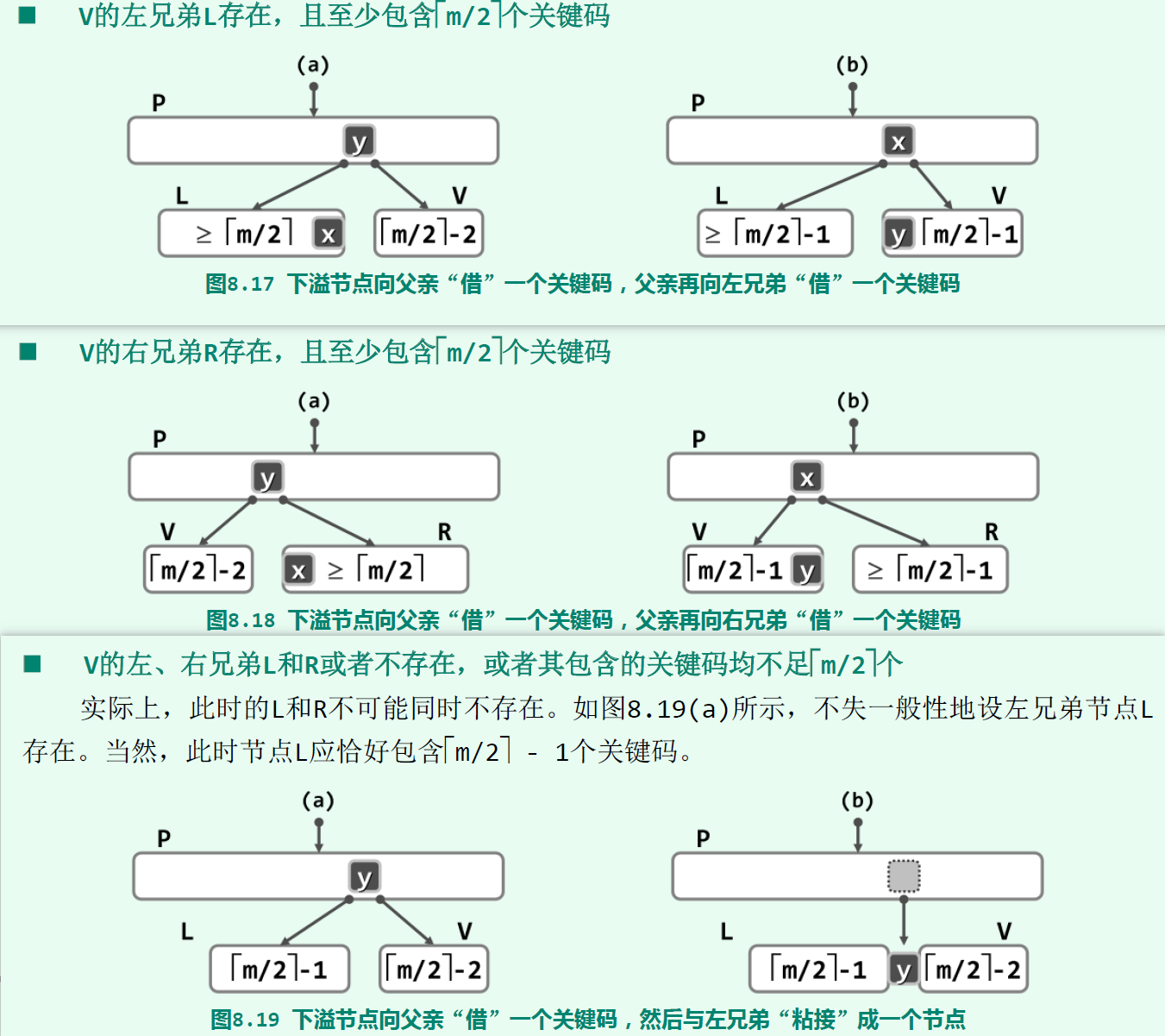
在删除一个key值时,思路和二叉搜索树的删除很像:找到待删除key值所在节点,将这个key值和它的直接后继(当前节点的孩子中大于这个key值的最小key值)交换,然后将key值删除。这种操作可以保证待删除key值所在节点是一个叶子节点。在删除完key值后,节点的key值数量可能会少于ceil(m/2)-1,发生了下溢,需要用合并操作处理。合并修复要分情况处理,假设待删除key值所在节点为V:
V存在左兄弟L,且至少包含ceil(m/2)个key值。那么,假设L和V是它们父节点P的key值y的左右孩子,将y移动到V(放在最左边),再将L中最大的key值x移动到y原本的位置,可以满足B-树条件。V的右兄弟R存在,且至少包含ceil(m/2)个key值。那么,作为上一种情况的镜像对称操作,也可以从R中挪用一个key值来顶替。V的左右兄弟L和R或者不存在,或者包含的key值均不足ceil(m/2)个。事实上,L和R不会同时不存在。假设L存在,它的key值数量应该刚好为ceil(m/2)-1。这时,可以从P中借来y,将L和V合并成一个节点。合并后的节点key值数量不大于m-1,满足B-树条件。然而,P的key值数量会减一,需要递归地对其检查是否下溢;如果下溢,还需对P进行合并修复。如果合并传递到了根节点,使其key值数量变为0,这时那个L V后的节点就成为了新根节点。
template <typename T, typename U>
struct MultiNode {
std::vector<T> keys;
std::vector<U> values;
int height;
MultiNode *parent;
std::vector<MultiNode*> children;
MultiNode() : parent(nullptr), height(0), children(1, nullptr) {}
};
template <typename T, typename U>
class MultiTree {
protected:
MultiNode<T, U> *root;
public:
MultiTree() : root(nullptr) {}
~MultiTree() { _delete(root); }
void _delete(MultiNode<T, U> *node) {
if (!node) return;
for (MultiNode<T, U>* child : node->children)
_delete(child);
delete node;
}
#define getHeight(node) ((node) ? (node)->height : -1)
void updateHeight(MultiNode<T, U> *node) {
int max_height = -1, child_height;
for (MultiNode<T, U>* child : node->children) {
child_height = getHeight(child);
if (child_height > max_height) max_height = child_height;
}
node->height = 1 + max_height;
}
};
template <typename T, typename U>
class BTree : public MultiTree<T, U> {
protected:
using MultiTree<T, U>::root;
int order; // m-order B-Tree
MultiNode<T, U> *_hot;
#define move_range(from,to,start) (to).assign((from).begin()+(start), (from).end()); (from).erase((from).begin()+(start), (from).end());
void solveOverflow(MultiNode<T, U> *node) {
if (node->children.size() <= order) return;
// move s-th key to parent node
int s = order / 2;
T key = node->keys[s];
U value = node->values[s];
// split to left and right child
MultiNode<T, U> *right = new MultiNode<T, U>();
move_range(node->keys, right->keys, s + 1); node->keys.pop_back();
move_range(node->values, right->values, s + 1); node->values.pop_back();
move_range(node->children, right->children, s + 1);
int i;
for (i = 0; i < right->children.size(); ++i)
if (right->children[i]) right->children[i]->parent = right;
// insert s-th key to parent
MultiNode<T, U> *parent = node->parent;
if (!parent) { // new root
parent = new MultiNode<T, U>();
root = parent;
root->children[0] = node;
}
for (i = 0; i < parent->keys.size(); ++i)
if (parent->keys[i] > key) break;
parent->keys.insert(parent->keys.begin()+i, key);
parent->values.insert(parent->values.begin()+i, value);
parent->children.insert(parent->children.begin()+i+1, right);
node->parent = parent; right->parent = parent;
solveOverflow(parent);
}
void solveUnderflow(MultiNode<T, U> *v) {
if ((order + 1) / 2 <= v->children.size()) return;
MultiNode<T, U> *p = v->parent;
if (!p) { // v is the root
if (!v->keys.size() && v->children[0]) {
// when merging the two children of root, root has only one key
root = v->children[0]; root->parent = nullptr;
delete(v);
}
return;
}
int i = 0; // v is the i-th child of p
while (p->children[i] != v) ++i;
if (0 < i) { // has left siblings
MultiNode<T, U> *L = p->children[i-1];
if ((order + 1) / 2 < L->children.size()) { // case 1
// move y and x
v->keys.insert(v->keys.begin(), p->keys[i-1]);
v->values.insert(v->values.begin(), p->values[i-1]);
p->keys[i-1] = L->keys.back(); p->values[i-1] = L->values.back();
L->keys.pop_back(); L->values.pop_back();
// and the last child of L
v->children.insert(v->children.begin(), L->children.back());
L->children.pop_back();
if (v->children[0]) v->children[0]->parent = v;
return;
}
} else if (p->children.size() - 1 > i) { // has right siblings
MultiNode<T, U> *R = p->children[i+1];
if ((order + 1) / 2 < R->children.size()) { // case 2
v->keys.insert(v->keys.end(), p->keys[i]);
v->values.insert(v->values.end(), p->values[i]);
p->keys[i] = R->keys[0]; p->values[i] = R->values[0];
R->keys.erase(R->keys.begin()); R->values.erase(R->values.begin());
v->children.push_back(R->children[0]);
R->children.erase(R->children.begin());
if (v->children.back()) v->children.back()->parent = v;
return;
}
}
// case 3
if (0 < i) { // merge with left sibling
MultiNode<T, U> *L = p->children[i-1];
// merge them to L. delete v
L->keys.push_back(p->keys[i-1]); L->values.push_back(p->values[i-1]);
p->keys.erase(p->keys.begin()+i-1); p->values.erase(p->values.begin()+i-1);
p->children.erase(p->children.begin() + i); // delete a branch
// move keys and children from v to L
L->keys.insert(L->keys.end(), v->keys.begin(), v->keys.end());
L->values.insert(L->values.end(), v->values.begin(), v->values.end());
L->children.insert(L->children.end(), v->children.begin(), v->children.end());
for (MultiNode<T, U> *child : L->children)
if (child) child->parent = L;
delete(v);
} else { // merge with right sibling
MultiNode<T, U> *R = p->children[i + 1];
R->keys.insert(R->keys.begin(), p->keys[i]);
R->values.insert(R->values.begin(), p->values[i]);
p->keys.erase(p->keys.begin() + i); p->values.erase(p->values.begin() + i);
p->children.erase(p->children.begin() + i);
// move keys and children from v to R
R->keys.insert(R->keys.begin(), v->keys.begin(), v->keys.end());
R->values.insert(R->values.begin(), v->values.begin(), v->values.end());
R->children.insert(R->children.begin(), v->children.begin(), v->children.end());
for (MultiNode<T, U> *child : R->children)
if (child) child->parent = R;
delete (v);
}
solveUnderflow(p);
}
public:
BTree(int order = 3) : MultiTree<T, U>(), order(order) {}
MultiNode<T, U>* search(T key) {
MultiNode<T, U> *curr = root;
_hot = nullptr;
int i;
while (curr) {
// search key in current node
for (i = 0; i < curr->keys.size(); ++i) {
if (curr->keys[i] == key) return curr;
else if (curr->keys[i] > key) break;
}
_hot = curr;
curr = curr->children[i]; // go to next node
}
return nullptr; // no such key
}
void insert(T key, U value) {
MultiNode<T, U> *node = search(key);
if (node) return; // has existed
if (!_hot) root = _hot = new MultiNode<T, U>();
int i;
for (i = 0; i < _hot->keys.size(); ++i) {
if (_hot->keys[i] > key) break;
}
// insert key at _hot->key[i]
_hot->keys.insert(_hot->keys.begin()+i, key);
_hot->values.insert(_hot->values.begin()+i, value);
// add a new child
_hot->children.insert(_hot->children.begin()+i+1, nullptr);
solveOverflow(_hot);
}
void remove(T key) {
MultiNode<T, U> *node = search(key);
if (!node) return; // no such node
// find key in node
int i;
for (i = 0; i < node->keys.size(); ++i) {
if (node->keys[i] == key) break;
}
if (node->children[0]) { // internal node
MultiNode<T, U> *u = node->children[i+1]; // right subtree
while (u->children[0]) u = u->children[0]; // direct succeed
node->keys[i] = u->keys[0]; node->values[i] = u->values[0];
node = u; i = 0; // go to the leaf node
}
// delete a key of leaf node
node->keys.erase(node->keys.begin()+i); node->values.erase(node->values.begin()+i);
node->children.erase(node->children.begin()+i+1);
solveUnderflow(node);
}
};
红黑树
红黑树(red-black tree)相较AVL树、伸展树,有一个明显的优势是它能在每次插入、删除后的重平衡过程中,全树拓扑结构更新仅涉及常数个节点。红黑树的“平衡”标准较AVL树更为宽松,大致为:任一节点左、右子树的高度,相差不得超过两倍。
红黑树树由二叉搜索树节点染成红色、黑色两种颜色而成。为了便利,我们将一棵二叉搜索树的所有节点称为内部节点,然后将它们的空孩子假想成是外部节点(都是叶子节点),使其成为真二叉树(每个内部节点都有两个孩子的二叉树)。如果由红黑两色节点组成的二叉搜索树满足以下条件,即为红黑树:
- 根节点始终为黑色
- 外部节点均为黑色
- 内部节点若为红色,则其孩子节点必为黑色
- 从任一外部节点到根节点的沿途,黑节点的数目相等
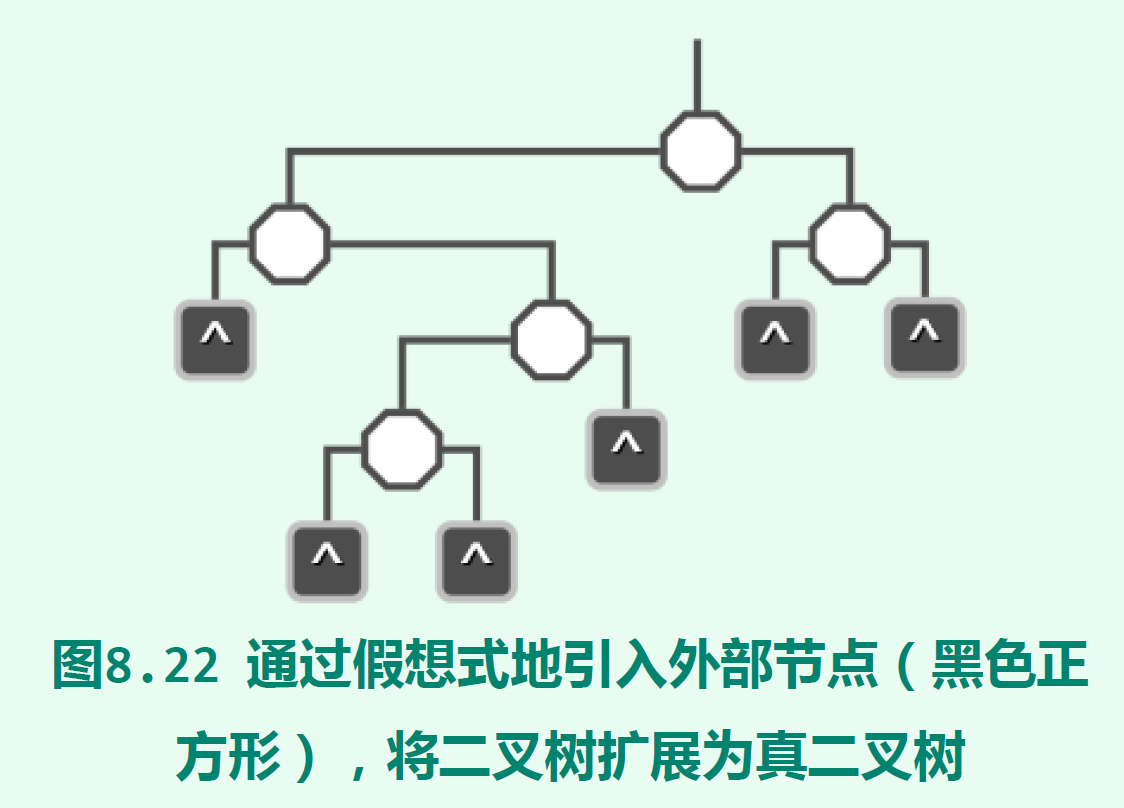
“外部节点”的概念只是为了染色和重平衡,在搜索、插入、删除操作上,红黑树和二叉搜索树没有本质的不同。在代码实现上我们可以对一个节点node判断if(!node),即判断node是否为空节点,如果是则认为它是一个外部节点,颜色为黑色。从根节点通往任一节点的沿途所经黑节点数(除去根节点)称为该节点的黑深度(black depth);从任一节点通往其任一后代外部节点的沿途所经黑节点数(除去黑色外部节点,通往哪个后代外部节点所经黑节点数总是一样)称为该节点的黑高度(black height)。从定义可以知道,所有外部节点的黑深度相等,根节点的黑高度(也是全树的黑高度)等于任一外部节点的黑深度。
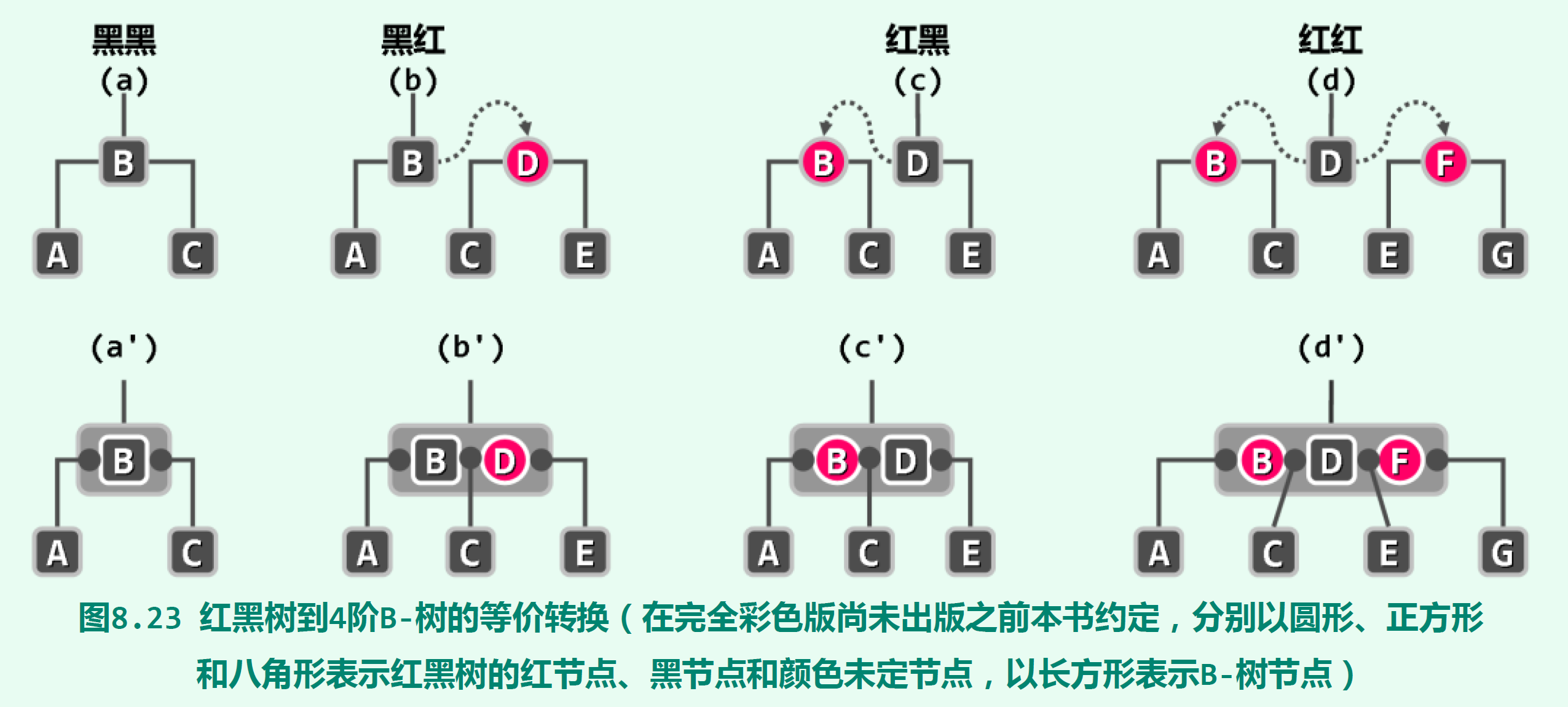
从定义上看,一棵红黑树是可以转换成等价的(2,4)-树的(即4阶B-树)。具体地,将每个黑色节点和它的红色孩子合并成一个节点即可完成转换。一个黑色节点有0到2个红色孩子,所以合并后的大节点有2到4个分支,符合4阶B-树的条件。根据对应(2,4)-树可以证明,若红黑树有n个内部节点,则它的高度h有:log_2(n+1)<= h<=2log_2(n+1),保证了红黑树可高效支持各种操作(O(logn时间内)。
红黑树的搜索和二叉搜索树的搜索没什么不同,因为本质上就是二叉搜索树,使用红黑染色仅是为了平衡高度。红黑树的插入操作会比较复杂,它规定每次插入的节点被染成红色(从二叉搜索树的插入实现可以知道,插入处总在叶子节点上。二叉搜索树的插入和红黑树的插入本质没什么不同,插入节点的父节点是一个已存在节点,即“内部节点”)。插入节点的父节点可能也是红色,这时会出现连续的两个红色节点,需要进行称之为“双红修正(RR-1)”的平衡操作。将触发双红修正的插入节点记为x,其红色父节点记为p,(必为黑色)祖父节点记为g,g的另一孩子(p的兄弟)记为u(可能为外部节点)。第一种双红修正的情况如下图,u为黑色节点:
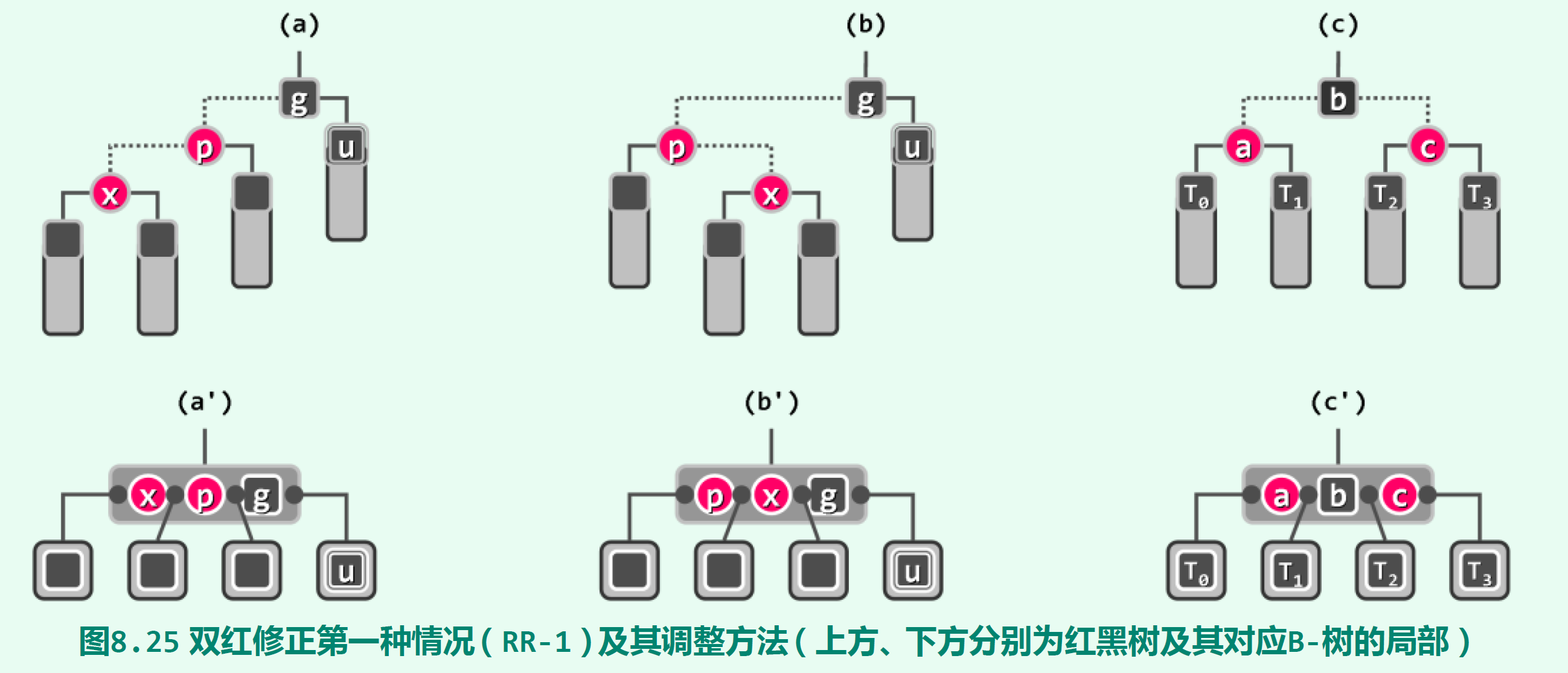
其中(a) (b)分别代表x为p左、右孩子的情况。将x p g三个节点合并为一个大节点( (a’) (b’) ),然后交换中间、右边两个节点的颜色,使三个节点按红、黑、红排列,如(c’),然后拆成等价的二叉树(c),即可完成平衡操作。可以看出,变换后的(c)和(a) (b)是等价的,它们的中序遍历序列都相等,并且满足红黑树的四个条件。
第二种双红修正的情况是u节点为红色,如下图:
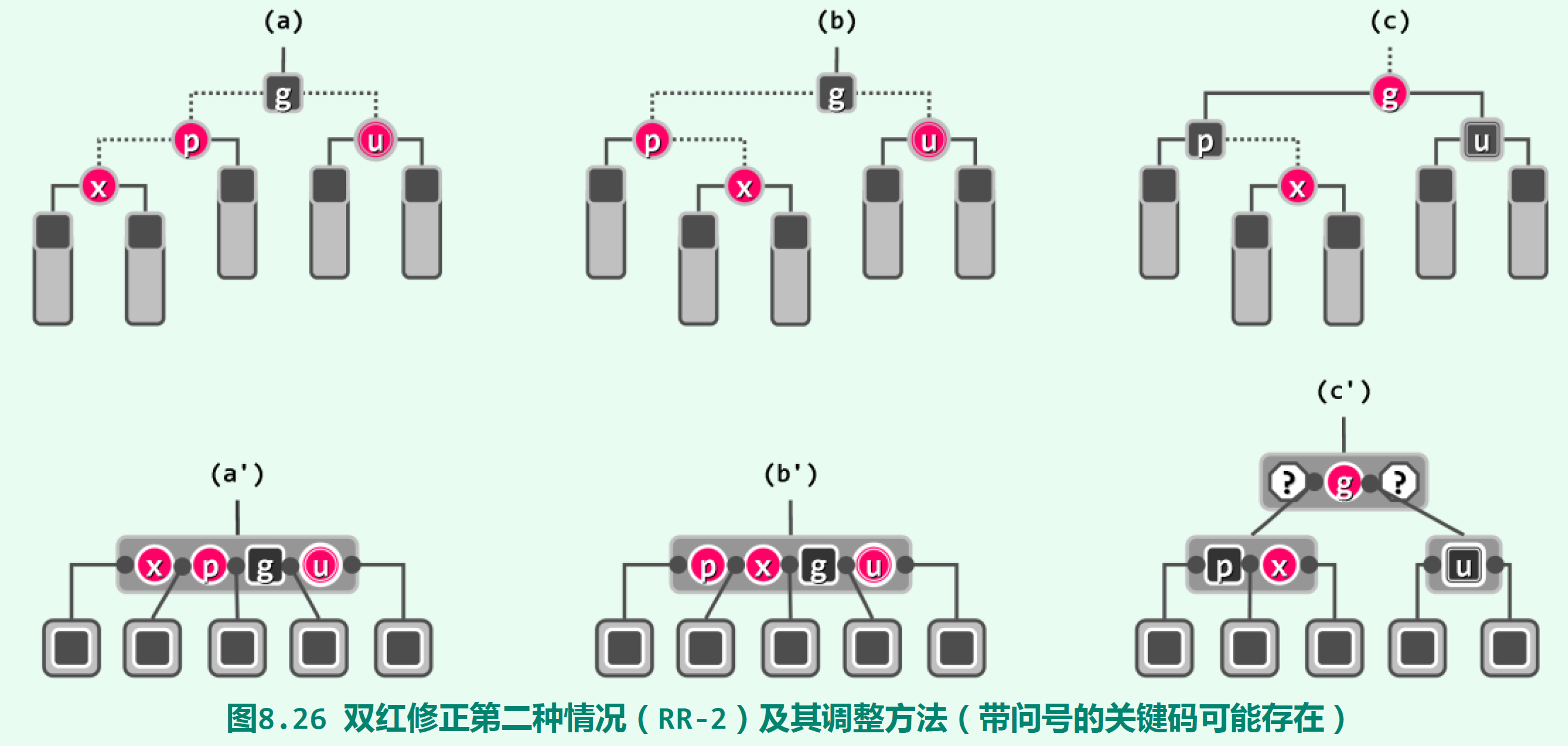
将g染成红色,它的两个孩子p u染为黑色。图中(c)是将(b)染色的一个例子,(a)是另一种情况,它对应的染色结果没有画出来。(a’) (b’) (c’)是染色前后的等价B-树,可以看出染色后依然满足红黑树条件。然而,g变成了一个红色节点,它的父节点有可能也是一个红色节点,这样g就又违背了红黑树条件,需要递归地对g重新做一次双红修正。
从(b)到(c),可以发现我们做的,仅仅是重新染色,甚至连旋转都没有。在u是红色的情况下,双红修正会向上传播,但是传播过程中只会染色,而不改变树的拓扑结构。等u是黑色以后,经过1-2次旋转,双红修正完成,因此需要改变结构的结构仅有常数个。下面会提到,红黑树在删除节点时,重平衡涉及的结构调整节点也只有常数个。对比AVL树,在删除过程中,需要调整结构的节点可能有O(logn)个,因此效率不及红黑树。
红黑树删除节点的过程和二叉搜索树删除的过程大致相同,删除的都是一个至多只有右孩子的节点。它的左孩子视为黑色外部节点。记被删节点为x,它的右孩子为r,它的父节点为p。在删除x以后,用r代替x的位置。这时,红黑树的条件可能会被破坏:
-
x为红色。删除x后红黑树条件依然满足。 x为黑色,r为红色,那么将r改成黑色,可以使p的黑高度不变,满足红黑树条件。x为黑色,r也为黑色。这时p的黑高度减一,可能会使p的祖先的黑高度不统一(即,到达各个外部节点途径黑色节点的数目不等)。这时需要进行进一步的“双黑修正”。
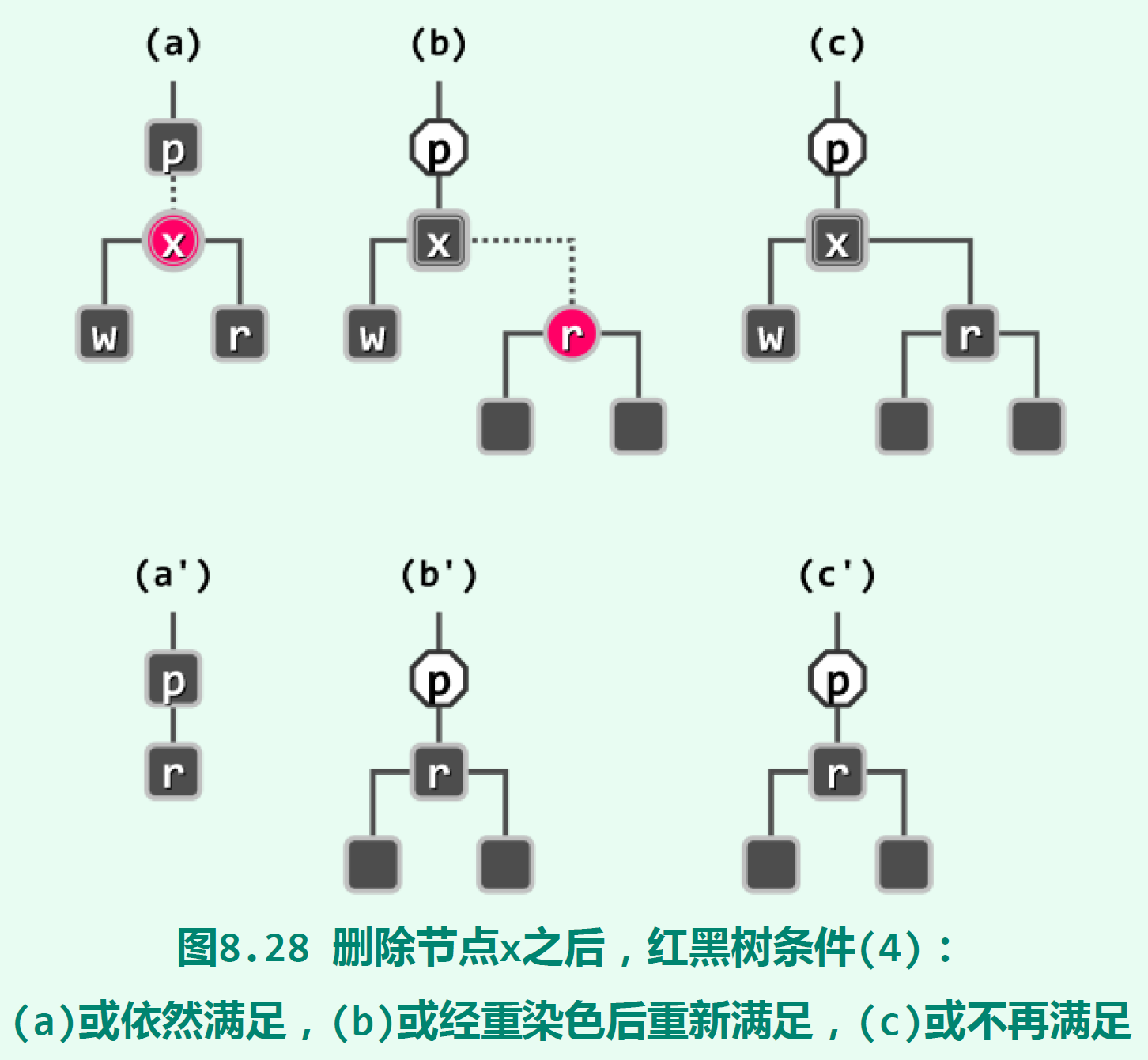
双黑修正和x的兄弟s相关。s必定存在,它存在以下几种可能,对其进行相应操作即可使树重新满足红黑树条件:
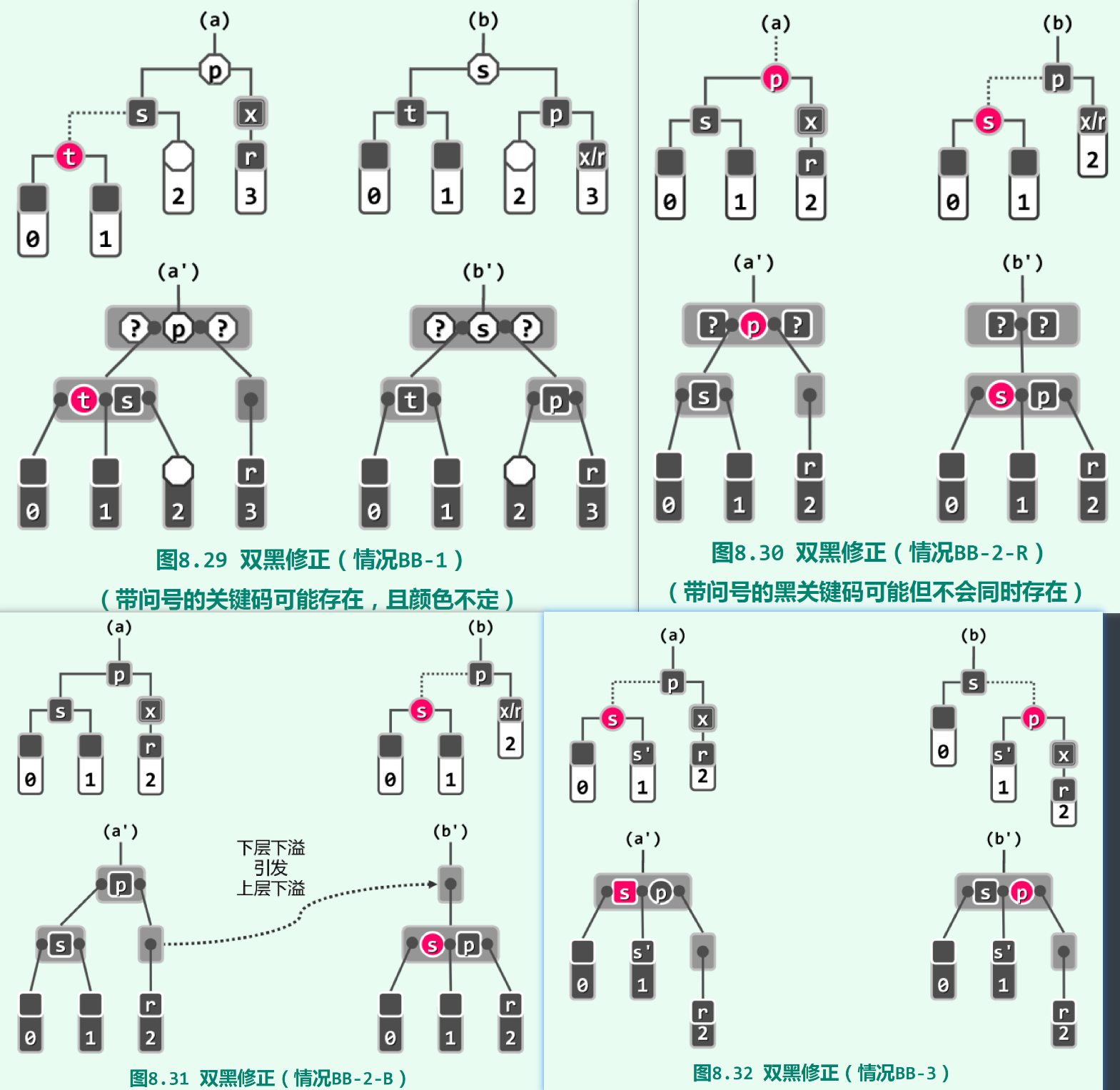
s为黑色,且存在红色孩子t:对t s p实施“3+4”重构。图8.29 (a)给出了一种情况(t为s左孩子),将s设为子树的根节点,s继承p的颜色,t p染为黑色。在t为s右孩子时,t设为子树的根节点,t继承p的颜色,s p染为黑色。拓扑结构的变化和AVL树的“3+4”重构相同。s和它的两个孩子均为黑色,p为红色:将s p颜色互换。s和它的两个孩子均为黑色,p为黑色:将s染红,(由于p的黑高度下降、B-树节点下溢),递归地对p进行双黑修复。s为红色,p为黑色:先对p进行zig旋转,并互换s p颜色,让子树变为第一、二种情况,按第一、二种情况的方式处理。
下图是以上情况的示意图。其中(a) (b) 是(a’) (b’)的B-树对应结构。以上变换都是基于B-树的重平衡策略,这里做简略处理,不解释B-树重平衡策略如何指导二叉树变换,仅列出变换方式。可以看到,仅第三种情况需要递归操作,向上传播双黑修正。然而在传播过程中,也只需要改变节点颜色,而不需要调整树拓扑结构。因此,双黑修正涉及的拓扑结构调整节点数也是常数个。