440. K-th Smallest in Lexicographical Order
Given integers
nandk, find the lexicographically k-th smallest integer in the range from1ton.Note: 1 ≤ k ≤ n ≤ 109.
Example:
Input: n: 13 k: 2 Output: 10 Explanation: The lexicographical order is [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9], so the second smallest number is 10.
将1到n的数字以前缀树的形式组织:

可以发现,所谓的字典序,其实就是前缀树的前序遍历而已。所以,要找到字典序的第k小的元素,即是找在前缀树前序遍历序列中第k个元素。假设我们现在处于元素curr,它离第k小的元素还有距离d。我们需要计算以curr为根节点的子树上的节点个数count。如果count >= d,那第k小的元素不会在这棵子树上,我们应该移动到以curr+1为根节点的子树上另做打算。如果count < d则说明第k小的元素在这棵子树上。我们令next = curr + 1。下面的一段代码中:
int count = 0; // count of nodes on subtree
while (curr <= n) {
count += next - curr;
next *= 10, curr *= 10;
}
在循环体中的每一步,计算了下一层中,子树拥有的节点数。在最后一层上,有可能n < next以致该层没有满节点,因此循环体中应该改为:
int count = 0; // count of nodes on subtree
while (curr <= n) {
count += min(next, n+1) - curr;
next *= 10, curr *= 10;
}
(注意,这段代码要计算的是,以curr为根节点的子树上的节点数量,而非讨论区高赞所说的“从curr移动到curr+1所需步数。以它的方法理解就会有一个逻辑上的问题:如果curr = 9,那么移动到curr+1便不是移动到右兄弟而是移动到下一层。虽然“移动”到curr = 9以后就实际上不可能再向右移动,但还是会带来思维上的困难)
在获取了当前子树的节点数后,如果count < d,那我们就向下搜索,移动到curr的第一个孩子。然后重复上面的操作,直到找到第k小的元素为止。
class Solution {
int nodesNum(long curr, long next, int n) {
int count = 0;
while (curr <= n) {
count += (n+1 > next ? next : n+1) - curr;
curr *= 10, next *= 10;
}
return count;
}
public:
int findKthNumber(int n, int k) {
int curr = 1, count;
--k; // 1 is the first element
while (k > 0) {
count = nodesNum(curr, curr+1, n);
if (count <= k) ++curr, k -= count; // move to curr+1
else curr *= 10, --k; // move to child
}
return curr;
}
};
351. 安卓系统手势解锁
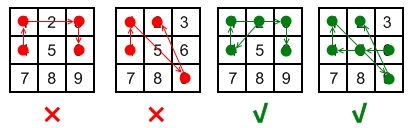
我们都知道安卓有个手势解锁的界面,是一个 3 x 3 的点所绘制出来的网格。
给你两个整数,分别为 m 和 n,其中 1 ≤ m ≤ n ≤ 9,那么请你统计一下有多少种解锁手势,是至少需要经过 m 个点,但是最多经过不超过 n 个点的。
先来了解下什么是一个有效的安卓解锁手势:
每一个解锁手势必须至少经过 m 个点、最多经过 n 个点。 解锁手势里不能设置经过重复的点。 假如手势中有两个点是顺序经过的,那么这两个点的手势轨迹之间是绝对不能跨过任何未被经过的点。 经过点的顺序不同则表示为不同的解锁手势。
解释:
无效手势:4 - 1 - 3 - 6 连接点 1 和点 3 时经过了未被连接过的 2 号点。
无效手势:4 - 1 - 9 - 2 连接点 1 和点 9 时经过了未被连接过的 5 号点。
有效手势:2 - 4 - 1 - 3 - 6 连接点 1 和点 3 是有效的,因为虽然它经过了点 2 ,但是点 2 在该手势中之前已经被连过了。
有效手势:6 - 5 - 4 - 1 - 9 - 2 连接点 1 和点 9 是有效的,因为虽然它经过了按键 5 ,但是点 5 在该手势中之前已经被连过了。
示例:
输入: m = 1,n = 1 输出: 9
这是一个DFS回溯问题。假设当前所处点为curr,且已经经过的点为len。如果len < n,我们需要找到下一个点next,作为DFS的下一个访问目标。这道题的难点就在于如何根据当前点判断下一个点是否有效。总得来说,next能分以下几种情况:
next已经被访问过,无效。next和curr相邻(上下左右 左上左下右上右下),有效。next和curr之间的移动是国际象棋中马的移动,即日字。有效。next和curr连线穿过第三个点,这个点被访问过->有效;这个点还未被访问过->无效。
class Solution {
int numberOfPatternsByLength(int curr, int len, vector<bool> &visited) {
// last visited node is curr, the length of path going to visit is len
if (len == 0) return 1; // end of path
int rtn = 0;
for (int i = 0; i < 9; ++i) {
if (isValid(curr, i, visited)) {
visited[i] = true;
rtn += numberOfPatternsByLength(i, len-1, visited);
visited[i] = false;
}
}
return rtn;
}
bool isValid(int curr, int next, vector<bool> &visited) {
// whether next is the valid point next to curr
if (visited[next]) return false;
if (curr == -1) return true; // first point
// knight moves or adjacent cells (in a row or in a column)
if ((curr + next) % 2) return true;
// curr and next are at 0 & 8 or 3 & 7
int mid = (curr + next) / 2;
if (mid == 4) return visited[mid];
// adjacent cells (on diagonal)
if ((curr % 3 != next % 3) && (curr / 3 != next / 3)) return true;
return visited[mid];
}
public:
int numberOfPatterns(int m, int n) {
vector<bool> visited(9, false);
int rtn = 0;
for (int len = m; len <= n; ++len) {
rtn += numberOfPatternsByLength(-1, len, visited);
}
return rtn;
}
};
726. Number of Atoms
Given a chemical
formula(given as a string), return the count of each atom.An atomic element always starts with an uppercase character, then zero or more lowercase letters, representing the name.
1 or more digits representing the count of that element may follow if the count is greater than 1. If the count is 1, no digits will follow. For example, H2O and H2O2 are possible, but H1O2 is impossible.
Two formulas concatenated together produce another formula. For example, H2O2He3Mg4 is also a formula.
A formula placed in parentheses, and a count (optionally added) is also a formula. For example, (H2O2) and (H2O2)3 are formulas.
Given a formula, output the count of all elements as a string in the following form: the first name (in sorted order), followed by its count (if that count is more than 1), followed by the second name (in sorted order), followed by its count (if that count is more than 1), and so on.
Example 1:
Input: formula = "H2O" Output: "H2O" Explanation: The count of elements are {'H': 2, 'O': 1}.Example 2:
Input: formula = "Mg(OH)2" Output: "H2MgO2" Explanation: The count of elements are {'H': 2, 'Mg': 1, 'O': 2}.Example 3:
Input: formula = "K4(ON(SO3)2)2" Output: "K4N2O14S4" Explanation: The count of elements are {'K': 4, 'N': 2, 'O': 14, 'S': 4}.
这道题和LeetCode 394有点类似,使用栈来保存之前尚未添加进结果集的元素,并用一个有序表来保存在当前层(和当前访问元素在同个括号内的元素算同一层)的元素。过程比较繁琐,尽量直接看代码:
class Solution {
public:
string countOfAtoms(string s) {
stack<map<string, int>> st;
map<string, int> curr;
int i = 0, count = 0; // index of current char, count of current element
// name of current element
string name;
while (i < s.length()) {
if (s[i] >= 'A' && s[i] <= 'Z') {
// get element name
name = s[i++];
if (i < s.length() && s[i] >= 'a' && s[i] <= 'z') {
name += s[i++];
}
// no decimal number -> count of element is 1
if (i >= s.length() || (i < s.length() && (s[i] < '0' || s[i] > '9')))
++curr[name];
} else if (s[i] >= '0' && s[i] <= '9') {
// count of current element
count = s[i++] - '0';
while (s[i] >= '0' && s[i] <= '9')
count = count * 10 + (s[i++] - '0');
curr[name] += count;
} else if (s[i] == '(') {
// next level. push current level into stack
st.push(curr), curr.clear(), ++i;
} else if (s[i] == ')') {
++i;
// count of current level
count = 0;
while (s[i] >= '0' && s[i] <= '9')
count = count * 10 + (s[i++] - '0');
if (count > 0) {
for (map<string, int>::iterator it = curr.begin(); it != curr.end(); ++it)
it->second *= count;
}
// append current level to previous level
for (map<string, int>::iterator it = st.top().begin(); it != st.top().end(); ++it)
curr[it->first] += it->second;
st.pop();
}
}
// empty the stack
if (!st.empty())
for (map<string, int>::iterator it = st.top().begin(); it != st.top().end(); ++it)
curr[it->first] += it->second;
// the result string
string rtn = "";
for (map<string, int>::iterator it = curr.begin(); it != curr.end(); ++it) {
rtn += it->first;
if (it->second > 1)
rtn += to_string(it->second);
}
return rtn;
}
};
135. Candy
There are N children standing in a line. Each child is assigned a rating value.
You are giving candies to these children subjected to the following requirements:
- Each child must have at least one candy.
- Children with a higher rating get more candies than their neighbors.
What is the minimum candies you must give?
Example 1:
Input: [1,0,2] Output: 5 Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.Example 2:
Input: [1,2,2] Output: 4 Explanation: You can allocate to the first, second and third child with 1, 2, 1 candies respectively. The third child gets 1 candy because it satisfies the above two conditions.
这是一个拓扑排序问题。对于当前小朋友i,如果ratings[i] > ratings[i-1],那么i获得的糖果数量就依赖于i-1获得的糖果数,要比后者多。这就像一个拓扑排序,i必须排在i-1后面。计算最少的糖果数,其实就是计算拓扑排序图中有多少层,以及每层有多少人。真的按拓扑排序的思路做,可以解决这个问题,不过耗时会比较久。更好的方法是这个答案里提到的,从左到右遍历一趟ratings,计算每个小朋友最低能获得多少个糖果。再从右到左遍历一趟,更新小朋友们能获得的最低糖果数。其实这是我上面拓扑排序思维的一个变种。链接下面评论有人称其为“wave”,我觉得很形象。
class Solution {
public:
int candy(vector<int>& ratings) {
vector<int> nums(ratings.size(), 1);
for (int i = 1; i < ratings.size(); ++i) {
if (ratings[i] > ratings[i-1]) nums[i] = nums[i-1] + 1;
}
for (int i = ratings.size() - 2; i >= 0; --i) {
if (ratings[i] > ratings[i+1]) nums[i] = nums[i] > (nums[i+1] + 1) ? nums[i] : (nums[i+1] + 1);
}
return accumulate(nums.begin(), nums.end(), 0);
}
};
887. Super Egg Drop
You are given
Keggs, and you have access to a building withNfloors from1toN.Each egg is identical in function, and if an egg breaks, you cannot drop it again.
You know that there exists a floor
Fwith0 <= F <= Nsuch that any egg dropped at a floor higher thanFwill break, and any egg dropped at or below floorFwill not break.Each move, you may take an egg (if you have an unbroken one) and drop it from any floor
X(with1 <= X <= N).Your goal is to know with certainty what the value of
Fis.What is the minimum number of moves that you need to know with certainty what
Fis, regardless of the initial value ofF?Example 1:
Input: K = 1, N = 2 Output: 2 Explanation: Drop the egg from floor 1. If it breaks, we know with certainty that F = 0. Otherwise, drop the egg from floor 2. If it breaks, we know with certainty that F = 1. If it didn't break, then we know with certainty F = 2. Hence, we needed 2 moves in the worst case to know what F is with certainty.Example 2:
Input: K = 2, N = 6 Output: 3Example 3:
Input: K = 3, N = 14 Output: 4
这道题可以用动态规划解决。令dp[k][n]为使用k个鸡蛋,从n层楼中找出F的最小移动数。假设在这n层楼中,我们选择楼层1 <= x <= n开始扔鸡蛋。如果鸡蛋破碎,说明F < x,[x, n]这些楼层可以排除。接下来的任务是利用k-1个鸡蛋,从x-1层楼中找出F,所需最小步数为dp[k-1][x-1]。如果鸡蛋没有碎,说明F >= x。接下来的任务是利用k个鸡蛋去[x+1, n]这些楼层尝试(第x层不再需要尝试。如果在第x+1层扔鸡蛋时破碎,说明F = x),所需最小步数为dp[k][n-x]。因此,在x层丢鸡蛋,所需的移动数为max(1 + dp[k-1][x-1], 1 + dp[k][n-x])。(至于为什么是max,我的想法是,题目要求保证能找到F的前提下的最小移动数。这是在求最低上限。求下限没有意义,因为运气好的话,我在N层楼中,随便挑一层楼x,在x和x+1各扔一次鸡蛋,一个碎一个没碎,就可以判断出F = x了。此时移动数的下限为2,它并没有实际的意义,因为移动2步不能保证对于任意初始值的F,都能找得出来。我们需要保证对任意初始值的F,都可以找出来,就要求移动数的上限。)由于dp[k-1][x-1]和dp[k][n-x]在求dp[k][n]前便已经计算过,所以我们可以确定在第x层扔鸡蛋,需要多少步才能确保找出F。我们考察1 <= x <= n的所有x,找出那个最小的步数,即是dp[k][n]的值。
初始时,dp[k][1] = 1,因为楼层只有一层楼,扔一次就可以;dp[1][n] = n,因为必须从1楼扔起,扔2楼扔3楼……最坏情况是一直扔到n楼。另外为了计算方便,设dp[k][0] = 0。完成初始化后,按下面的代码更新dp数组:
class Solution {
public:
int superEggDrop(int K, int N) {
vector<vector<int>> dp(K+1, vector<int>(N+1));
for (int k = 0; k <= K; ++k) dp[k][0] = 0, dp[k][1] = 1;
for (int n = 1; n <= N; ++n) dp[1][n] = n;
for (int k = 2; k <= K; ++k) {
for (int n = 2; n <= N; ++n) {
dp[k][n] = 0x7fffffff;
for (int x = 1; x <= n; ++x) {
dp[k][n] = min(dp[k][n], 1 + max(dp[k-1][x-1], dp[k][n-x]));
}
}
}
return dp[K][N];
}
};
这个算法的时间复杂度为O(KN^2),非常高,提交LeetCode以后会超时。因此,需要对时间复杂度进行一些优化。事实上,由于dp[k][n]是随着n递增而递增的,所以在最内层循环中,dp[k-1][x-1]会随着x递增而递增,dp[k][n-x]会随着x递增而递减。想象一下,一开始时x = 1,应该是dp[k-1][x-1] <= dp[k][n-x],它们的最大值是dp[k][n-x]。随着x递增,这两个函数会相遇,之后最大值变成了dp[k-1][x-1]。显然,这两个函数越靠近时,它们的最大值就越小。因此,最大值应该是呈下降->上升趋势。要找最大值的最小值,可以用二分查找。内层循环的复杂度变为O(lgN),算法整体的复杂度也下降到了O(KNlgN)。
int lo = 1, hi = n;
while (lo + 1 < hi) {
x = (lo + hi) / 2;
if (dp[k-1, x-1] < dp[k, n-x]) lo = x; // 交点在左边
else if (dp[k-1, x-1] > dp[k, n-x]) hi = x; // 交点在右边
else lo = hi = x; // 发现了交点
}
// 这个官方提供的二分查找保留了两个候选项lo和hi
// 事实上因为dp[k-1, x-1]和dp[k, n-x]是离散的,可能没有交点,所以二分查找要在lo = hi - 1
// 且dp[k-1, lo-1] < dp[k, n-lo] && dp[k-1, hi-1] > dp[k, n-hi]处停下。lo和hi正好在交点两边
ans = 1 + min(max(dp[k-1, lo-1], dp[k, n-lo]), max(dp[k-1, hi-1], dp[k, n-hi]));
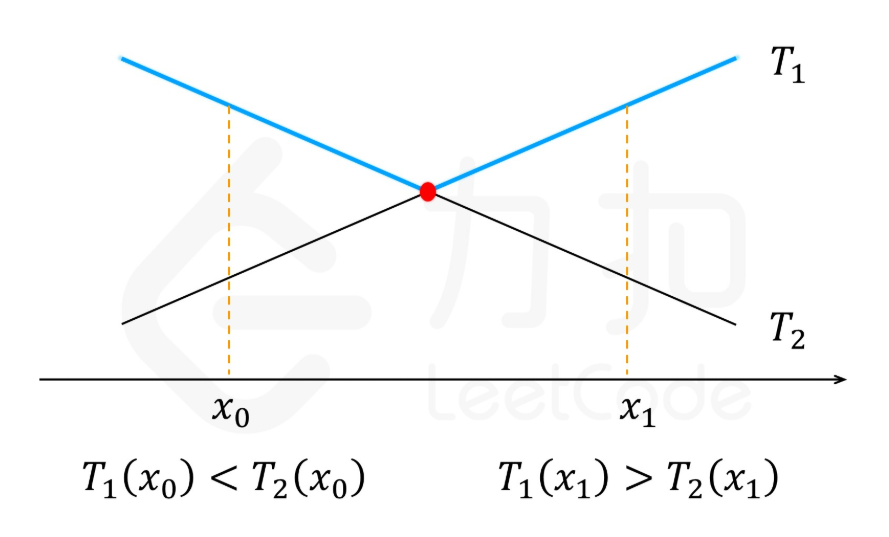
上面的状态转移方程意图是让我们寻找点
当n增加时,dp[k-1][x-1]不变,dp[k][n-x]增加。由于我们是寻找这两个函数的交点。我们可以把T1 = dp[k-1][x-1]想象成是一条斜率为正的线,T2 = dp[k][n-x]是一条斜率为负的线。n增加,T2抬高。这时交点会向右移。因此,在第二层循环for (int n = 2; n <= N; ++n)中,如果已经算得n的$x_{opt}$,那么要计算n+1的x_{opt}时,只需从n的$x_{opt}$开始计算。上述算法可以改进成下面,时间复杂度进一步减少到O(KN):
class Solution {
public:
int superEggDrop(int K, int N) {
vector<vector<int>> dp(K+1, vector<int>(N+1));
for (int k = 0; k <= K; ++k) dp[k][0] = 0, dp[k][1] = 1;
for (int n = 1; n <= N; ++n) dp[1][n] = n;
for (int k = 2; k <= K; ++k) {
int x = 1;
for (int n = 2; n <= N; ++n) {
// max(dp[k-1][x-1], dp[k][n-x]还在呈下降趋势
while (x < n && max(dp[k-1][x-1], dp[k][n-x]) > max(dp[k-1][x], dp[k][n-x-1]))
++x;
dp[k][n] = 1 + max(dp[k-1][x-1], dp[k][n-x]);
}
}
return dp[K][N];
}
};
另外,在空间复杂度上也可以进行优化。二维数组dp可以用两个一维数组代替,一个记录dp[k-1]一个记录dp[k]。
在官方回答中,还提到了一种理论上时间复杂度更小的办法。这种方法也是动态规划,不过它求的是:给定T次移动和K个鸡蛋,最多能检测的楼层数N = f(T, K)。对于一个T,如果f(T, K)不小于题目给的N,那么说明可以用T步来找出题目中所说的F。因此,我们就把题目转化成:求满足f(T, K) >= N的最小的T。
f(T, K)的转移方程比较难想。假设有一栋楼高M,至少用T次移动和K个鸡蛋才能测出它的F。那么f(T, K) = M。我们在这栋楼的某一层扔鸡蛋,假如它碎了,我们就排除当前楼层上面的楼层,专注于下面的楼层。下面的楼层的高度Md显然是等于f(T-1, K-1),因为测出下面楼层的F,是测出整栋楼F的一个环节。反之,如果鸡蛋没碎,那么当前楼层下面楼层就被排除,我们专注于上面的楼层。上面楼层的高度显然是f(T-1, K),原理和前面的情况一样。因此,整栋楼的高度f(T, K) = f(T-1, K-1) + f(T-1, K) + 1。
边界条件为:当T >= 1的时候,f(T, 1) = T,当K >= 1的时候,f(1, K) = 1。显然,T <= N。我们只需计算f(1, 1)到f(N, K)的所有值,找出其中不小于N的最小的T即可。由于找到了T程序就会返回,所以理论上的时间复杂度是小于O(KN)的。(官方结论是$O(K*\sqrt[K]{N})$。
class Solution {
public:
int superEggDrop(int K, int N) {
if (N == 1) return 1;
vector<vector<int>> f(N + 1, vector<int>(K + 1));
for (int i = 1; i <= K; ++i) f[1][i] = 1;
int ans = -1;
for (int i = 2; i <= N; ++i) {
for (int j = 1; j <= K; ++j)
f[i][j] = 1 + f[i - 1][j - 1] + f[i - 1][j];
if (f[i][K] >= N) {
ans = i;
break;
}
}
return ans;
}
};
89. Gray Code
The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
Example 1:
Input: 2 Output: [0,1,3,2] Explanation: 00 - 0 01 - 1 11 - 3 10 - 2 For a given n, a gray code sequence may not be uniquely defined. For example, [0,2,3,1] is also a valid gray code sequence. 00 - 0 10 - 2 11 - 3 01 - 1Example 2:
Input: 0 Output: [0] Explanation: We define the gray code sequence to begin with 0. A gray code sequence of n has size = 2n, which for n = 0 the size is 20 = 1. Therefore, for n = 0 the gray code sequence is [0].
显然,n位格雷码的数量是n-1位格雷码的数量的两倍。在求出n-1位格雷码以后,在第n位加一个1,就能转变成n位格雷码。由于相邻两个格雷码的汉明距离为1,所以可以把n-1位格雷码序列颠倒,然后在第n位加一个1,再和原序列拼接。这样拼接后的序列,相邻两个格雷码的汉明距离仍然是1。
class Solution {
public:
vector<int> grayCode(int n) {
if (n == 0) return {0};
vector<int> codes = grayCode(n-1), copy = codes;
reverse(copy.begin(), copy.end());
int n_bit = 1 << (n - 1);
for (int &i : copy) i += n_bit;
codes.insert(codes.end(), copy.begin(), copy.end());
return codes;
}
};
54. Spiral Matrix
Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
Example 1:
Input: [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ] Output: [1,2,3,6,9,8,7,4,5]Example 2:
Input: [ [1, 2, 3, 4], [5, 6, 7, 8], [9,10,11,12] ] Output: [1,2,3,4,8,12,11,10,9,5,6,7]
这题不难,关键是要写得优雅。这个答案写得就挺好:
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector <int> ans;
if(matrix.empty()) return ans; //若数组为空,直接返回答案
int u = 0; //赋值上下左右边界
int d = matrix.size() - 1;
int l = 0;
int r = matrix[0].size() - 1;
while(true) {
for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
if(++ u > d) break; //重新设定上边界,若上边界大于下边界,则遍历遍历完成,下同
for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
if(-- r < l) break; //重新设定有边界
for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
if(-- d < u) break; //重新设定下边界
for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
if(++ l > r) break; //重新设定左边界
}
return ans;
}
};
43. Multiply Strings
Given two non-negative integers
num1andnum2represented as strings, return the product ofnum1andnum2, also represented as a string.Example 1:
Input: num1 = "2", num2 = "3" Output: "6"Example 2:
Input: num1 = "123", num2 = "456" Output: "56088"
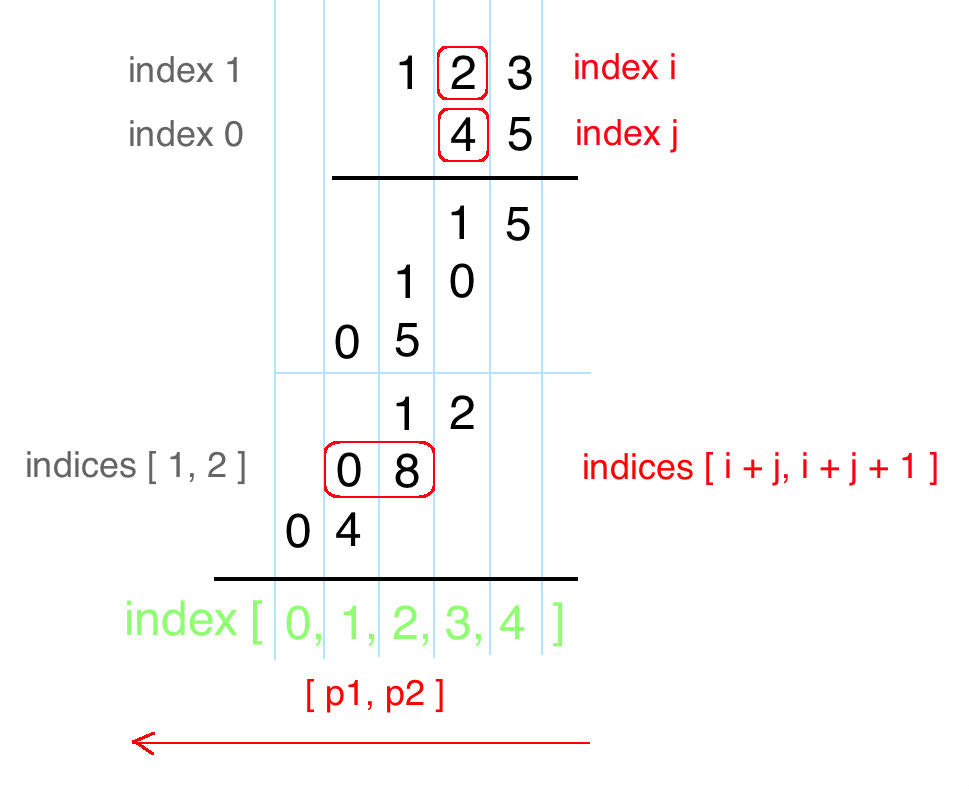
num1的第x位(从低位数起,最低位是第0位)和num2的第y位相乘,相乘结果乘以10^(x+y)加在最后的乘积中。两个数相乘,结果最多是num1.length() + num2.length()位。因此,可以用一个长度为num1.length() + num2.length()的数组暂时保存每位的相乘结果,最后再将数组转变成字符串。
class Solution {
public:
string multiply(string num1, string num2) {
if (num1 == "0" || num2 == "0") return "0";
int l1 = num1.length(), l2 = num2.length(), n1, n2;
vector<int> rtn(l1 + l2, 0);
for (int i = l1 - 1; i >= 0; --i) {
n1 = num1[i] - '0';
for (int j = l2 - 1; j >= 0; --j) {
n2 = num2[j] - '0';
// num1[i]是num1的第l1-i-1位,num2[j]是num2的第l2-j-1位,因此在rtn中是第l1+l2-i-j-2位。
// rtn第0位下标是l1+l2-1,因此第l1+l2-i-j位下标是(l1+l2-1)-(l1+l2-i-j-2) = i+j+1。
n2 = n1 * n2 + rtn[i + j + 1];
rtn[i + j + 1] = n2 % 10, rtn[i + j] += n2 / 10; // 进位
}
}
string srtn = "";
for (int i = 0; i < rtn.size(); ++i) {
if (i == 0 && rtn[i] == 0) continue; // 跳过首部0
srtn += rtn[i] + '0';
}
return srtn;
}
};
913. Cat and Mouse
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.
The graph is given as follows:
graph[a]is a list of all nodesbsuch thatabis an edge of the graph.Mouse starts at node 1 and goes first, Cat starts at node 2 and goes second, and there is a Hole at node 0.
During each player’s turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node
1, it must travel to any node ingraph[1].Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
Then, the game can end in 3 ways:
- If ever the Cat occupies the same node as the Mouse, the Cat wins.
- If ever the Mouse reaches the Hole, the Mouse wins.
- If ever a position is repeated (ie. the players are in the same position as a previous turn, and it is the same player’s turn to move), the game is a draw.
Given a
graph, and assuming both players play optimally, return1if the game is won by Mouse,2if the game is won by Cat, and0if the game is a draw.Example 1:
Input: [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] Output: 0 Explanation: 4---3---1 | | 2---5 \ / 0
这道题官方的回答是用极大极小算法(不是很懂),我看了另一篇答案,用的是通俗易懂的动态规划。令dp[t][x][y]表示走t步以后(猫和老鼠一起算,t % 2 == 0表示现在轮到老鼠走,t % 2 == 1表示现在轮到猫走),老鼠处于节点x,猫处于节点y的胜负情况。0表示平局,1表示老鼠胜利,2表示猫胜利,-1表示未知。以下这些情况,猫和老鼠的胜负情况是确定的:
dp[*][0][*],即老鼠走入洞中,老鼠胜利,值为1dp[*][y][y],即猫和老鼠在同个位置,猫胜利,值为2dp[2n][*][*],其中n为节点数,即猫和老鼠都走遍了所有节点,平局,值为0。这里用t <= 2n为中止条件,而非题目所说的不可进入以前走过的节点,可以简化问题。
根据下一轮的胜负情况,我们可以回推当轮的胜负情况。
-
如果
t % 2 == 0,当轮老鼠行动,下一轮猫行动。递归地探索所有老鼠能到达的节点nx in graph[x]:- 如果有某个
nx使得dp[t+1][nx][y] == 1,那么当前轮中,老鼠只要走入nx节点,它就获胜了,所以dp[t][x][y] = 1,表示老鼠当前轮稳赢。 - 如果对于所有
nx都有dp[t+1][nx][y] == 2,说明当前轮中,无论老鼠走到哪里,它都输定了,所以dp[t][x][y] = 2,表示老鼠当前轮稳输。 - 其他情况下,有些
nx使得dp[t+1][nx][y] == 0,有些(也许没有)nx使得dp[t+1][nx][y] == 2。老鼠肯定不会那么傻,走去dp[t+1][nx][y] == 2的那些nx节点。它会走到平局的那些节点去,所以dp[t][x][y] = 0。
- 如果有某个
-
同理,如果
t % 2 == 1,当轮猫行动,下一轮老鼠行动。我们也有类似的结论:-
对于一个
ny in graph[y],如果它等于0,我们应该跳过它,因为猫不能进入0节点。 - 如果有某个
ny使得dp[t+1][ny][y] == 2,那么当前轮中,猫只要走入ny节点,它就获胜了,所以dp[t][x][y] = 2,表示猫当前轮稳赢。 - 如果对于所有
ny都有dp[t+1][ny][y] == 1,说明当前轮中,无论猫走到哪里,它都输定了,所以dp[t][x][y] = 1,表示猫当前轮稳输。 - 其他情况下,有些
ny使得dp[t+1][ny][y] == 0,有些(也许没有)ny使得dp[t+1][ny][y] == 1。猫肯定不会那么傻,走去dp[t+1][ny][y] == 1的那些ny节点。它会走到平局的那些节点去,所以dp[t][x][y] = 0。
-
根据这些状态转移式子,可以从顶向下地搜索游戏每一步的胜负状态。最后,只要返回dp[0][1][2](开始时的胜负)就可以了。
class Solution {
int recursive(vector<vector<vector<int>>> &dp, vector<vector<int>> &graph, int t, int x, int y, int n) {
if (t >= 2 * n) return 0;
if (x == y) return 2;
if (x == 0) return 1;
if (dp[t][x][y] != -1) return dp[t][x][y];
int next;
if (t % 2 == 0) {
bool catWin = true;
for (int nx : graph[x]) {
if ((next = recursive(dp, graph, t + 1, nx, y, n)) == 1)
return dp[t][x][y] = 1; // set dp[t][x][y] = 1 and return
if (next == 0)
catWin = false;
}
if (catWin) return dp[t][x][y] = 2; // all dp[t+1][nx][y] == 2, mouse loses
else return dp[t][x][y] = 0;
} else {
bool mouseWin = true;
for (int ny : graph[y]) {
if (ny == 0) continue; // cat cannot go to 0
if ((next = recursive(dp, graph, t + 1, x, ny, n)) == 2)
return dp[t][x][y] = 2;
if (next == 0)
mouseWin = false;
}
if (mouseWin) return dp[t][x][y] = 1;
else return dp[t][x][y] = 0;
}
return -1; // cannot reach here
}
public:
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
vector<vector<vector<int>>> dp(2 * n, vector<vector<int>>(n, vector<int>(n, -1)));
return recursive(dp, graph, 0, 1, 2, n);
}
};
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
这题是非常基础的动态规划题,大一新生就会做。这里主要是想说一种叫线段树的做法。设get_sums(l, r)为nums[l:r+1]中的四个求和:以nums[l]为左端点的最大子数组和lsum,以nums[r]为右端点的最大子数组和rsum,nums[l:r+1]中的最大子数组和msum,以及nums[l:r+1]所有元素的和esum。这道题要求的是get_sums(l, r).msum。我们可以分治地求不同l r的这四个求和。如果l == r,那么显然这四个求和都是nums[l]。如果l < r,我们可以令mid = (l + r) >> 1,将其分为两部分:nums[l:mid+1]和nums[mid:r+1]。递归地求出这两部分的四个求和left和right。那么,
lsum = max(left.lsum, left.esum + right.lsum)。如果lsum对应子数组只在left部分中,那么它就是left.lsum;如果它跨越了left来到了right,那么它就是left.esum + right.lsum。rsum = max(right.rsum, right.esum + left.rsum)。原理和lsum相同。esum = left.esum + right.esum,毫无疑问。msum = max(max(left.msum, right.msum), left.rsum + right.lsum)。如果msum对应子数组只存在于left中,那么它就是left.msum;如果只存在于右数组中,那么它就是right.msum。如果它跨越了left和right,那么它应该是left.rsum + right.lsum。
class Solution {
struct sums {
int lsum, rsum, msum, esum;
};
sums get_sums(vector<int>& nums, int l, int r) {
if (l == r) return { nums[l], nums[l], nums[l], nums[l] };
int mid = (l + r) >> 1;
sums left = get_sums(nums, l, mid), right = get_sums(nums, mid + 1, r);
int lsum = max(left.lsum, left.esum + right.lsum),
rsum = max(right.rsum, right.esum + left.rsum),
esum = left.esum + right.esum,
msum = max(max(left.msum, right.msum), left.rsum + right.lsum);
return { lsum, rsum, msum, esum };
}
public:
int maxSubArray(vector<int>& nums) {
return get_sums(nums, 0, nums.size() - 1).msum;
}
};