Morris Traversal
Morris Traversal是一种时间复杂度为O(n),空间复杂度为O(1)的中序遍历方法。它的特点是,在到达一个节点后,找它的“predecessor”:它左子树下最靠右的节点。也就是在中序遍历序列中,访问当前节点之前访问的节点。这个predecessor的右孩子应该是空的,所以可以把它设成当前节点。当遍历过程到达predecessor那里后,可以直接通过右孩子指针回到中序遍历下的下一个节点。这样就不需要额外的栈空间来存储它要返回的节点。
在Morris Traversal中,每条边最多被访问两次(一次用来找predecessor,一次用来确认predecessor已经访问过)。在最坏的情况下,有|V|条边被创建,其中|V|是节点数。
# Iterative function for inorder tree traversal
def MorrisTraversal(root):
# Set current to root of binary tree
current = root
while current:
if not current.left:
# reach the leftmost node
print(current.val)
# go to the right subtree or back to root
current = current.right
else:
# Find the inorder predecessor of current
pre = current.left
while (pre.right and pre.right != current):
pre = pre.right
if not pre.right:
# Make current as right child of its inorder predecessor
pre.right = current
# go to next node
current = current.left
else:
# we have built the link between the current node and its predecessor.
# The only case is that we visited the predecessor in the last step,
# and came to the current node by its right child pointer.
# Therefore, visit current node and go to its right subtree
pre.right = None
print(current.val)
current = current.right
KMP算法
著名的看毛片算法。KMP算法用来做子字符串匹配。具体地说,就是在一个字符串s中,找出所有与另一字符串p相等的子串。KMP算法能做到在O(n)时间复杂度里完成匹配。
KMP算法先算一个跟p有关的lps数组(longest prefix, suffix),其中lps[i]是p[:i+1]的最长的共同前缀后缀子串的长度。如果有一个子字符串是p[:i+1]的前缀,同时也是后缀,那么它就称为共同前缀后缀子串(简称前后缀。前后缀不能是p[:i+1]本身,起码要比p[:i+1]少一个字符。比如abcd的前缀有a, ab, abc。)这个lps的好处是,当我们匹配时,p[:i]和s[j:j+i]都匹配上了,但是p[i] != s[j+i],我们不必回到s[j+1]和p[0]那里重新匹配过,而是向前移动i-lps[i-1]距离:
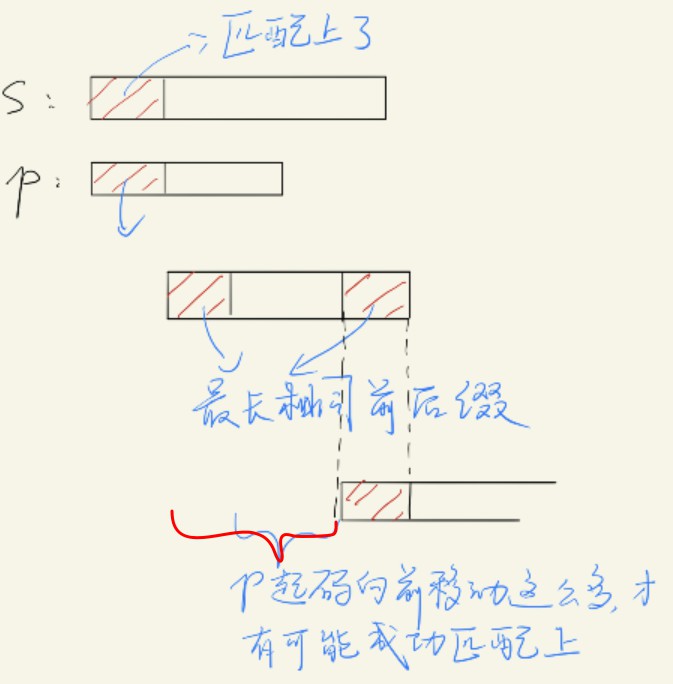
因为p[:i]中有长度为lps[i-1]的前后缀,所以移动距离i-lps[i-1]能让p[:i]再次匹配上i-lps[i-1]个字符。(注意,移动p其实是移动指针j。p首部和s[j]对齐)为什么是移动这么多距离,而不能是更少呢?因为移动更少距离,p[:i]没有机会和s[j:]匹配上。设想一下,如果真的匹配上了,p[:i]应该有一个更长的最长前后缀才对。在移动完j以后,s[j:j+lps[i-1]]跟p[:lps[i-1]]是匹配上的,下一步我们应该考虑s[j+lps[i-1]]是否等于p[lps[i-1]],所以我们要把p的指针i移到lps[i-1]。
def KMPSearch(p, s):
M = len(p)
N = len(s)
lps = [0] * M
i = 0 # index for p
# Preprocess the pattern (calculate lps[] array)
computeLPSArray(p, M, lps)
j = 0 # index for s
while j < N:
if p[i] == s[j]:
j += 1
i += 1
if i == M:
print("Found pattern at index " + str(j - i))
i = lps[i - 1]
else:
# mismatch after i matches
# Do not match lps[0..lps[i-1]] characters, they will match anyway
if i != 0:
i = lps[i - 1]
else:
# p[0] != s[j]. move j forward
j += 1
在求lps是也可以做优化。比方说,我们已经算出p[:i]的lps值是len,那么如果p[len]==p[i],就能确定lps[i] = len+1。这看图很容易看出来。

如果p[len]!=p[i],说明p[:i+1]的最长前后缀的前缀(下面就简称最前缀和最后缀)不是p[:len+1],而是包含在p[:len]里。我们用a b c d来标明p的最前缀和最后缀上的四个长度相等子串(可能是空串)。

我们想找一个最长的a,来使得它后一个字符是p[i],并且a+p[i]是p[:i+1]的最前缀。但是呢,a b和c d是在p[:i]的最前后缀中,所以有a==c和b==d。这样的话,a的长度就不能超过p[:len]的最前缀。否则,a!=b -> a!=d -> a+p[i]!=d+p[i],这个a+p[i]就不是p[:i+1]的最前缀。因此,a被包含在p[:len]的最前缀中。因此,在计算lps[i]时,不用再考虑其最前缀长度大于p[:len]最前缀长度(即lps[len-1])的情况。
def computeLPSArray(p, M, lps):
len = 0 # length of the previous longest prefix suffix
# lps[0] is always 0. the loop calculates lps[i] for i = 1 to M-1
i = 1
while i < M:
if p[i] == p[len]:
# situation in figure 2.
len += 1
lps[i] = len
i += 1
else:
if len != 0:
# like recursion!
len = lps[len - 1]
else:
# p[i] != p[0]. no common prefix-suffix
lps[i] = 0
i += 1
Floyd-Warshall 算法
| FW算法是一个动态规划的求最短路径的算法。和Dijkstra不同,它能求出所有顶点到所有顶点的最短距离,时间复杂度是$O( | V | ^3)$,如果要用Dijkstra实现求所有顶点到所有顶点的最短路径,时间复杂度是$O( | V | ^2 | E | )$。FW算法用$dist(i, j, k)$来表示,从节点i到节点j,经过编号为1-k的中间节点,能达到的最短路径长度。在已知所有$dist(\cdot, \cdot, k-1)$的情况下,我们知道,节点i到j的最短路径有两种可能: |
- 经过
k,那么$dist(i, j, k) = dist(i, k, k-1) + dist(k, j, k-1)$。这是因为这条最短路径上,只有1-k号点,而点k只会经过一次(没有负权重边) - 不经过
k,那么$dist(i, j, k) = dist(i, j, k-1)$
一开始,$dist(i, j, 0)$在i到j之间有边的情况下设为边权重,否则设为无穷大。然后逐步迭代:
N = len(V)
dist = [[[float('inf') for _ in range(N+1)] for _ in range(N+1)] for _ in range(N+1)]
for edge in E:
dist[edge.start][edge.end][0] = edge.weight
for k in range(1, N+1):
for i in range(1, N+1):
for j in range(1, N+1):
dist[i][j][k] = min(dist[i][j][k-1], dist[i][k][k-1] + dist[k][j][k-1])
最大流算法
(以下复制了一些在上本科离散数学课做的笔记)
- 运输网络transport_network是具有如下性质的一个连通有向图
N:- 存在唯一一个入度为0的结点,称为源source。通常对源结点标号为1。
- 存在唯一一个出度为0的结点,称为汇sink。如果
N有n个结点,通常对汇标号n。 - 图N已被标号,在边
(i,j)上的标号$C_{ij}$是一个非负数,称为边的容量capacity。 (为了简单起见,流量都往一个方向,即顶点之间只有一条有向边)
- N中的流flow是一个函数,使N中每条边
(i,j)都指定一个不超过$C_{ij}$的非负数$F_{ij}$ - 进入结点k的边上的$F_{ik}$之和必须等于离开结点k的边上的$F_{kj}$之和,这称为流的守恒conservation of flow。离开源的流之和等于进入汇的流之和,称为流量value of flow,记作value(F)。
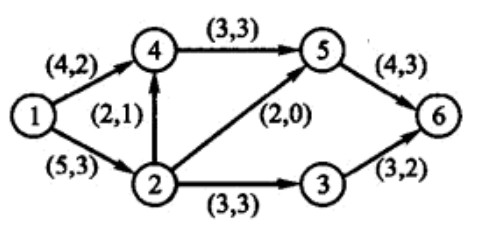
(两个数字是正负超容量)
标号算法labelling_algorithm(找最大流):
设N是有n个结点的一个网络,G是N的对称闭包。在G中选择一条道路和该道路上一条边(i,j),如果(i,j)属于N,$e_{ij}=C_{ij}-F_{ij}>0$,则称该边有正的超容量。如果(i,j)不是N中的边,此时如果$F_{ji}>0$,则称(i,j)有超容量$e_{ij}=F_{ji}$,于是通过边(i,j)的增流将产生减少$F_{ji}$的结果。
算法:
- 设$N_1$是通过一条具有正的超容量边与源相连接的所有结点集合,$N_1$中每个j标记$[E_j,1]$,其中$E_j$是边
(1,j)上的超容量$e_{1j}$. - 设$N_1$中的结点j是有最小节点号的结点,$N_2(j)$表示所有未标号的(除源外)与j相连并且有正的超容量的结点集合。假设结点k属于$N_2(j)$并且
(j,k)是有正的超容量的边,则k标记$[E_k,j]$,其中$E_k$是 $E_j$ 和 边(j,k)上超容量$e_{jk}$ 的最小值。当$N_2(j)$中所有结点都用这种方法标号后,对$N_1$中其他结点重复该过程,设$N_2=\cup_{j\in N_1}N_2(j)$. - 重复2,给$N_3,N_4,\cdots$标号。直到下列情形之一出现:
(i) 汇没有得到标号并且没有其他结点可以标号。 —> 算法终止,总流就是最大流。
(ii) 汇得到标号$[E_n,m]$,其中$E_n$是通过道路$\pi$到达汇的额外流量。以相反次序检查$\pi$,如果边$(i,j)\in N$,则在(i,j)上增流$E_n$,并且减少相同量的超流量$e_{ij}$。同时给(虚)边
(j,i)增加超流量$E_n$。而如果$(i,j)\not \in N$,则在(j,i)上减少流$E_n$,并且增加它的超容量$E_n$,同时在(i,j)上减少相同量的超容量。现在得到一个新的比前面大$E_n$个单位的流,并回到1。
- N的切割cut定义为某些边的集合
K,它的从源到汇的每条道路至少包含K中的一条边(就是说,一个切割把N分成两块,一块有源,一块有汇)。一个切割K的容量,即$c(K)$,是K中所有边的容量之和。
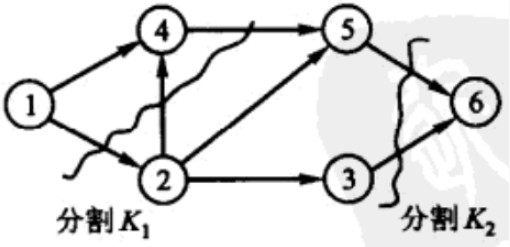
任意流F的$value(F)$总不大于任意切割的$c(K)$。
- 最大流最小割定理max_flow_min_cut_theorem:在一个网络中最大流F与该网络中最小切割容量相等。标号算法产生最大流的原因就是最大流最小割定理。
from collections import defaultdict
def max_flow(node_num, edges):
# node_num: num of nodes in the graph
# edges[i]: {j: wj, h: wh, ...}, edges[i][j] is the capacity from i to j
# nodes must be encoded with integers from 1 to node_num
G = defaultdict(dict) # transitive closure
for i, value in edges.items():
for j, w in value.items():
G[i][j] = w
G[j][i] = 0
total_flow = 0
while True:
# start from N_1
# current labels of nodes
labels = {}
N_next = set()
for j in G[1].keys():
if G[1][j] > 0:
labels[j] = (G[1][j], 1)
N_next.add(j)
N_i = N_next
N_next = set()
while len(N_i) > 0:
for i in N_i:
for j in G[i].keys():
if j not in labels and G[i][j] > 0 and j != 1:
# hasn't been labelled and accessible
labels[j] = (min(G[i][j], labels[i][0]), i)
N_next.add(j)
if node_num in labels.keys():
break
N_i = N_next
N_next = set()
if node_num in labels.keys():
# the sink has been labelled. update the graph
current_flow = labels[node_num][0]
total_flow += current_flow
a, b = labels[node_num][6], node_num
while a != 1:
G[a][b] -= current_flow
G[b][a] += current_flow
a, b = labels[a][7], a
G[a][b] -= current_flow
G[b][a] += current_flow
else:
# terminate
return total_flow
在遍历图时,其实是一个BFS,可以用队列来优化一下。
将2维动态规划转化为1维动态规划
很多时候,2维动态规划(使用二维数组来存储中间计算值)都可以转成1维动态规划,1维动态规划可以转成常数空间复杂度。 这是因为计算dp[i]往往只依赖于dp[:i](很多时候只依赖于dp[i-1]),所以用临时变量来存储上一步的结果就好了。2维动态规划转1维动态规划的也是同理,用一个一维数组来存储上一排中间计算值结果。一般来说,去掉axis=0那个维度比较简单。一般循环是
for i in range(d1):
for j in range(d2):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
这样的。用一个临时数组来储存dp[i-1]就好了。如果想去掉axis=1维度,可以转置一下矩阵,反正每一步迭代,dp只依赖于当前位置左上方的那些位置,在计算次序上转置和不转置是一样的。
一下是一个LeetCode的[例子][https://leetcode.com/problems/wildcard-matching/]:
class Solution:
def isMatch(self, s, p):
# dp. dp[i][j] is True if p[:j] can match s[:i]
m, n = len(s), len(p)
dp = [[False for _ in range(n+1)] for _ in range(m+1)]
dp[0][0] = True
for i in range(1, m+1):
# empty pattern could not match any non-empty string
dp[i][0] = False
# only '*', '**' can match an empty string
for j in range(1, n+1):
if p[j-1] != '*':
break
dp[0][j] = True
for i in range(1, m+1):
for j in range(1, n+1):
if p[j-1] != '*':
dp[i][j] = dp[i-1][j-1] and (p[j-1] == '?' or s[i-1] == p[j-1])
else:
dp[i][j] = dp[i-1][j] or dp[i][j-1]
return dp[m][n]
class Solution:
def isMatch(self, s, p):
# dp. dp[i][j] is True if p[:i] can match s[:j]
m, n = len(p), len(s)
dp = [[False for _ in range(n+1)] for _ in range(m+1)]
dp[0][0] = True
# only '*', '**' can match an empty string
for i in range(1, m + 1):
if p[i - 1] != '*':
break
dp[i][0] = True
for j in range(1, n+1):
# empty pattern could not match any non-empty string
dp[0][j] = False
for i in range(1, m+1):
for j in range(1, n+1):
if p[i-1] != '*':
dp[i][j] = dp[i-1][j-1] and (p[i-1] == '?' or s[j-1] == p[i-1])
else:
dp[i][j] = dp[i-1][j] or dp[i][j-1]
return dp[m][n]
Counting Sort
Counting Sort 计数排序使用一个数组,来计算待排序数组的元素的频数。比如说,数组[1,3,2,2], 最大值为3,使用长度为4的数组count来统计频数。统计完后,count[i]表示数i在数组中出现的次数。对count每一项count[i]都进行:count[i] += count[i - 1]。这样,count[i]就表示数组中不大于数i的数的个数。因此,在排序好的数组中,数i应该放在位置count[i]-1上。
def countingsort(arr):
# can store the count of elements ranging from 0 to 10
count = [0] * 11
for each in arr:
count[each] += 1
for i in range(1, len(count)):
count[i] += count[i - 1]
output = [0] * len(arr)
for each in arr:
output[count[each] - 1] = each
count[each] -= 1
return output
并查集 union-find (disjoint-set)
并查集应该谁都知道吧……非常优美的算法。为记录而记录。
class DisjointSet:
def __init__(self, max_size):
self.parent = list(range(max_size))
def find(self, x):
return x if self.parent[x] == x else self.find(self.parent[x])
def union(self, x1, x2):
self.parent[self.find(x1)] = self.find(x2)
def is_same(self, x1, x2):
return self.find(x1) == self.find(x2)
用栈做先序/中序/后序遍历
鉴于这个知识点还是考得挺多的,自己也没有一下子精准写出来的智商(虽然原理不难),所以就把它也写出来以供复习。
我觉得,为了让自己思维不混乱,首先要对“栈里装的是什么”这个问题有清晰的认识。
首先是先序遍历。先序遍历在访问完当前节点后,会移动到左子树,而右子树的根节点需要记录下来在栈中,等待之后访问。由于右子树们是由下至上访问的,符合栈LIFO的特质,所以把右孩子都压进栈即可。这时,栈里装的是“待遍历的(右)子树的根节点”。因此从栈中pop出来节点后,只需按preorder流程访问、压节点入栈即可。
def preorderTraversal(self, root: TreeNode):
stack = [root]
while stack:
# traverse the subtree whose root is node / preorder(node)
node = stack.pop()
while node:
if node.right:
stack.append(node.right)
visit(node)
node = node.left
中序遍历和后序遍历会稍微复杂一点。中序遍历优先访问左孩子,所以一棵子树中,最先被访问的一定是那个“最左”的节点,也就是从根节点一直向左,直到无法再左的节点。到达这个节点后,访问之,然后就去遍历它的右子树;然后,退回它的父节点,访问父节点,然后访问父节点的右子树……可以看到,这个过程中,“父节点”们是从下至上被访问的,适合储存在栈中。这时,栈中存储的是“左子树被遍历过,而根节点和右子树尚未被遍历的子树的根节点”。从栈中取出一个节点后,要先访问它,然后对它的右孩子进行inorder操作。为了简化代码,我们可以把“最左”节点也当成“左子树被访问过,而根节点和右子树尚未被访问的子树的根节点”,并把它们也压入栈中。
def inorderTraversal(self, node: TreeNode) -> List[int]:
stack = []
while node or stack:
# if node, traverse the subtree whose root is node / inorder(node)
# if not node, go to stack.pop()
while node:
# go to the left most node, and store parent nodes
stack.append(node)
node = node.left
# now node is the left most node, or the last parent node
node = stack.pop()
# visit node, and then go to its right subtree
visit(node)
# if node.right is None, the "while node" step would just skip
# and the stack could pop the last parent node
node = node.right
后序遍历也是从“最左”节点开始访问。我们可以模仿中序遍历,一路直达最左节点,将路上的父节点都存在栈中。在遍历完一棵左子树后,从栈中弹出一个节点,即左子树的父节点。下一步,遍历这个父节点的右子树。这里存在一个重要的问题:父节点何时被访问呢?在遍历完左子树后,会从栈中取出父节点一次,进入它的右子树;在遍历完右子树后又需要到达父节点,访问之。这意味着被存在栈中的父节点总共需要被取出2次。因此,在第一次取出时,不能将其pop,第二次就无法找回它了。只有在一个父节点被访问完后,我们才能将其pop。另外,我们也注意到,将一个节点从栈中pop出来,代表着以它为根节点的子树已经完整遍历完。因此,在我们pop出一个节点的右孩子后,它的左、右子树都遍历完了,下一个被访问的就是它自己。它被访问完后pop掉。所以,如果一个栈顶节点的右孩子是上一个被pop的节点,那么它就会被访问,然后被pop;否则,意味着它的右子树还未被遍历,进入它的右子树。至此,我们可以总结:栈中存储的是“左子树被遍历过,右子树可能被遍历过,根节点尚未被访问的子树的根节点”。判断右子树是否被遍历,要看上一个被pop的节点是否为当前节点的右孩子。
def postorderTraversal(self, node: TreeNode) -> List[int]:
if not node:
return []
self.rtn = []
stack = []
last = None # last popped node
while node or stack:
# if node, traverse the subtree whose root is node / postorder(node)
# if not node, go to stack.pop()
while node:
# go to the left most node, and store parent nodes
stack.append(node)
node = node.left
# now node is the left most node, or the last parent node
node = stack[-1]
# whether its right child has been visited
# pop all nodes whose right subtree has been traversed
while not node.right or node.right == last:
# the right child has been visited
self.visit(node)
last = stack.pop()
if stack:
# go to the last unvisited node
node = stack[-1]
else:
# all nodes has been visited
return self.rtn
# go to the right subtree
node = node.right
后序遍历的另一种方法,是对前序遍历进行改造。使用类似前序遍历的节点->右节点->左节点的顺序遍历树,得到的遍历序列是后序遍历的翻转。
def postorderTraversal(self, root: TreeNode):
stack = [root]
while stack:
# traverse the subtree whose root is node / preorder(node)
node = stack.pop()
while node:
if node.left:
stack.append(node.left)
visit(node)
node = node.right
用队列做层序遍历
void levelTraversal(TreeNode *node) {
queue<TreeNode*> q;
q.push(node);
while (!q.empty()) {
int size = q.size();
while (size--) {
visit(q.front());
if (q.front()->left) q.push(q.front()->left);
if (q.front()->right) q.push(q.front()->right);
q.pop();
}
}
}
背包问题
01背包问题
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
令f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。对于第i件物品,可以选择放,也可以选择不放:
for i = 1..N
for v = 0..V
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]};
如果要求“恰好将背包装满”,则初始化时将f[0][0]设为0,f[0][1...V]设为-inf。如果不要求背包恰好装满,则初始化时将f[0][0...V]全部设为0。这是因为,f[0][0...V]表示没有任何物品可以放入背包下的合法状态。要求“恰好装满”,则只有f[0][0]是有效的,其他容量都是无效的,不能从其递推出f[1...N][0...V]。
由于我们最终想要的只有f[N][V],当i = N时(外层迭代最后一轮),我们不必计算f[N][0..V-1]。为了计算f[N][V],我们需要知道f[N-1][V]和f[N-1][V-c[N]]。因此,在i = N-1那一轮,我们不必计算f[N-1][0..(V-c[N]-1)]。为了计算f[N-1][V-c[N]],我们需要知道f[N-2][V-c[N]]和f[N-2][V-c[N]-c[N-1]]。因此,在i = N-2那一轮,我们也不必计算f[N-1][0..(V-c[N]-c[N-1]-1)]。总结这个规律,可以发现,在i = n那一轮,我们不必计算f[N-1][0..(V-sum(c[(i+1)..N])-1)]。我们可以将循环下标改成
for i = 1..N
for v = (V-sum(c[(i+1)..N]))..V
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]};
同时,v至少要比c[i]大。所以循环下标可以进一步改成
for i = 1..N
for v = max{(V-sum(c[(i+1)..N])), c[i]}..V
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]};
求得f[N][V]的时间空间复杂度都是O(VN)。现在尝试将f改成一维数组,使空间复杂度降为O(V)。由于f[i][v]依赖f[i-1][v-c[i]],如果逆序地遍历V..0,就能避开这个依赖:
for i=1..N
for v=V..max{(V-sum(c[(i+1)..N])), c[i]}
f[v]=max{f[v],f[v-c[i]]+w[i]};
int zero_one_pack(vector<int> &c, vector<int> &w, int N, int V) {
vector<int> f(V+1, 0);
int sum_w = accumulate(c.begin(), c.end(), 0);
for (int i = 1; i <= N; ++i) {
sum_w -= c[i];
for (int v = V, bound = max(V-sum_w, c[i]); v >= bound; --v)
f[v] = max(f[v], f[v-c[i]] + w[i]);
}
return f[V];
}
完全背包问题
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
每件物品可以取用无限次,按照01背包问题的思路,状态转移方程为:
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v}
这个方程的计算量是非常大的,我们必须对此做改进。f[i][v]表示取前i件物品(每个物品可以取0~无限次)放进大小为v的背包,可以取得的最大收益。那么,显然f[i][v] >= f[i-1][v],即第i件物品取0件时的收益。如果第i件物品取1~inf件,设此时最大的利益为profit,那么在这些物品中拿走一个第i件物品,则最大收益变成profit - w[i]。这个最大收益,可以表示成”取前i件物品(每个物品可以取0~无限次)放进大小为v - c[i]的背包可以获得的最大收益,即f[i][v-c[i]]。因此,profit = f[i][v-c[i]] + w[i]。综上,f[i][v] = max{f[i-1][v], f[i][v-c[i]] + w[i]}。这个转移方程和01背包问题的转移方程很像,只是第二项从f[i-1][v-c[i]]变成了f[i][v-c[i]]。将f简化成一维数组:
for i=1..N
for v=0..V
f[v]=max{f[v],f[v-c[i]]+w[i]};
注意到内层循环不再是V..0而是0..V了,因为f[i][v]不再依赖f[i-1][v-c[i]]而是依赖f[i][v-c[i]]。
多重背包问题
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
多重背包问题和完全背包问题很像,状态转移方程为
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k<=n[i]}
完全背包问题和多重背包问题都有一种共同的做法——将复杂的完全背包和多重背包转换成01背包问题。多于第i件物品,至多可以取n[i]件,那么就用n[i]件相同的物品代替。最终变成总共sum(n[1..N])件物品的背包问题,时间复杂度从O(VN)变成O(V\sum n[i])。事实上,每个n[i]可以表示为至多k个数的和,这k个数为arr_k = [1 2 4 ... 2^(k-1) n[i]-2^k+1]。k是满足n[i]-2^k+1>0的最大整数。将n[i]件物品转化成k件物品,其中第x件的重量为c[i] * arr_k[x],价值为w[i] * arr_k[x]。注意到这k件物品能组合出的所有重量、价值,和n[i]件原物品可以组合出的重量、价值是一样的。在这k件物品中挑选和原来的n[i]件物品中挑选没什么不同。这里使用的是二进制的思想,