异或链表
异或链表是双向链表的一种变体。它并不需要像双向链表那样,每个节点保存两个地址,一个指向前节点一个指向后节点。它只需要保存前节点地址和后节点地址的异或值。在从前向后遍历中,已知两个相邻节点的地址(用B和C代表前后两个节点)。C的异或值和B的地址异或,就得到了C下一个节点的地址。因此,遍历能够继续进行。异或链表的缺点就是必须知道相邻至少两个节点的地址,才能完成对链表的遍历。
堆
堆heap排序我经常用(优先队列……),但是让我手写一个堆排序,我老是会把细节忘记。
首先普通的binary堆是一个完全二叉树。最大堆中,所有节点的值都不小于子节点的值。而在最小堆中,所有节点的值都不大于子节点的值。在给堆添加、删除节点后,一般都要heapify堆,让它维持堆的性质。heapify有点类似树版的冒泡排序。以最大堆为例,不满足堆性质的节点(比如比父节点更大的节点)会从底部冒上来(顶替父节点),到达它应该的位置。下面代码中的heapify是一种通常的做法,它必须在子树都已经heapify好后才能对根节点heapify。
在堆排序(降序)过程中,首先要将数组建成一个最大堆。做法是让数组变成一棵完全二叉树,然后heapify每个节点。建成堆后,数组的最大值就在根节点的位置。将根节点移除输出,然后用堆最底层最后一个节点来顶替根节点并进行heapify,反复此过程,直到所有节点都输出。每次最大堆输出的都是当前堆里的最大值,因此输出序列便是一个递减序列,完成排序。
在实现中,一般会用一个一维数组来代表堆。这是因为堆是一个完全二叉树,i号节点(从上往下、从左往右数)的子节点的编号是2i+1和2i+2,直接通过数组索引便可访问子节点,不需通过指针等。同时,为了不增加计算空间,输出过程是把根节点和堆最后一个节点交换。在排序完毕后,最大堆产生升序排序,最小堆产生降序排序,跟理想中的算法顺序是不一样的。
代码实现如下:
def heapify(arr, n, i):
# heapify the ith node in the heap arr, whose length is n
left, right = 2 * i + 1, 2 * i + 2
largest = i # largest node within i, 2i+1 and 2i+2
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
if largest != i:
# swap the root with the largest node
arr[largest], arr[i] = arr[i], arr[largest]
heapify(arr, n, largest)
def heap_sort(arr):
for i in range(len(arr)//2-1, -1, -1):
heapify(arr, len(arr), i)
# output nodes
for i in range(len(arr)-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
void heapify(vector<int> &arr, int begin, int end) {
int tmp;
while (begin < end) {
int left = begin * 2 + 1, right = begin * 2 + 2;
int max = begin;
if (left < end && arr[left] > arr[max]) max = left;
if (right < end && arr[right] > arr[max]) max = right;
if (max != begin) tmp = arr[max], arr[max] = arr[begin], arr[begin] = tmp, begin = max;
else break;
}
}
void heapSort(vector<int> &arr) {
int tmp;
for (int i = arr.size() / 2 - 1; i >= 0; --i) {
heapify(arr, i, arr.size());
}
for (int i = arr.size() - 1; i > 0; --i) {
tmp = arr[0], arr[0] = arr[i], arr[i] = tmp;
heapify(arr, 0, i);
}
}
Trie树
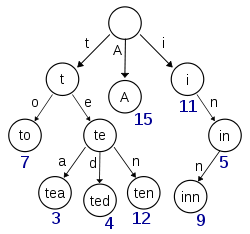
Trie树翻译叫前缀树、字典树,可以用来快速地检索单词。Trie树非常简单易懂,每个节点对应一个字母,每个字典里的单词都是Trie树从根节点都某个叶子节点路径上的字母的拼凑。因为Trie树的特点,它在自动补全输入单词时有很大的用处。有一题LeetCode涉及了Trie树的构造和应用,可以看看当时我自己是怎么做的。