介绍
Part B: Optimizing Matrix Transpose 则比较复杂,需要较多的思考,所以我想把对它的理解记录下来,免得以后忘记了。简单地说,Part B 要求我们转置一个给定的矩阵A,将结果保存在另一矩阵B中。必须要cache miss少于一定值才能通过该实验。测试脚本使用的cache simulator参数为s = 5, E = 1, b = 5,即直接映射,有2^5 = 32个set,每个set 1行,block大小为2^32 = 32字节。在三个测试用例中,矩阵A和B的形状分别是32*32, 64*64, 61*67。在运行test-trans启动测试后,会生成一个valgrind trace文件trace.f0。该文件大概长这样:
S 0038b08c,1
L 0038b0a0,8
L 0038b084,4
L 0038b080,4
L 0030b080,4
S 0034b080,4
L 0030b0a0,4
S 0034b084,4
L 0030b0c0,4
S 0034b088,4
在我测试多种矩阵形状后,我发现trace.f0有种特定模式(我不能保证总是这样,这只是个经验性的结论):
- 从第5行开始,会重复出现一个load一个store。通过计数,我认为load的是
A[i][j],store的是B[j][i]。 - 第一个访问的元素是
A[0][0]B[0][0]的话,第5行的地址总是0030b080,第6行的地址是0034b080。所以可以认为AB的起始地址分别是0030b080和0034b080。
32 * 32
我们先从测试用例32*32开始,对这两个矩阵的地址进行分析。最简单的转置方法什么也不考虑,直接进行转置:
void trans(int M, int N, int A[N][M], int B[M][N]) {
int i, j;
for (i = 0; i < N; ++i) {
for (j = 0; j < M; ++j) {
B[j][i] = A[i][j];
}
}
}
这种暴力的方法miss数为1183。我们运用附带资料里的blocking方法进行优化。
由于block大小为32字节,足够存放8个整形数,所以每次从内存读入A[i][j]时,会把它左右的共8个数一起读入一个block(在资料里,这种一行的小block叫做row sliver。之后我也会用row sliver指代一个block,而block这次词则指一个bsize*bsize的子矩阵)。举个例子,A[0][0:8]会被读入同个row sliver,写入set 00100 中。A[0][8:16]则读入另一个row sliver,写入set 00101 中,以此类推。根据row sliver大小为32字节这一信息,我们可以先写一个粗糙的blocking优化转置算法,将bsize设置为8的倍数是比较合适的,这样同一个row sliver最少只用读进一次:
void trans(int M, int N, int A[N][M], int B[M][N]) {
int i, j, ii, jj;
int bsize = 8;
for (jj = 0; jj < M; jj += bsize) {
for (ii = 0; ii < N; ii += bsize) {
for (i = ii; i < ii + bsize; ++i) {
for (j = jj; j < jj + bsize; ++j) {
B[j][i] = A[i][j];
}
}
}
}
}
这个原始的blocking算法miss数为343,相比暴力方法高效了很多,但是离<300的满分标准还是差一些。因此,我们需要对A B两个矩阵做更近一步的分析。
假如我们把A[0][0:8]编号为1号row sliver,A[0][8:16]编号为2号row sliver……A[1][0:8]编号为5号row sliver,A[1][8:16]编号为6号row sliver……A[32][24:32]编号为32 * 4 = 128号row sliver。由于set共32个,所以编号对32取模相等的row sliver会被放入同一个set中。同样的,B[0][0:8]也是被放入 00100 set中。B[i][j]和A[i][j]共用同一个set,如果我们需要在数步内同时访问A[i][j]和B[i][j],就很可能发生conflict miss。幸好在转置算法中,我们需要同时访问的是A[i][j]和B[j][i]。而A[i][j]所在的row sliver,只可能和A[i+8][j], A[i+16][j], A[i+24][j]所在row sliver发生冲突。如果A[ii][jj:jj+bsize]不在矩阵对角线上的话,B[jj:jj+bsize][ii]是不可能和A[ii][jj:jj+bsize]发生冲突的,因为它在对角线的另一边,而可能和A[ii][jj:jj+bsize]发生冲突的row sliver都在同一列上。因此,在对非对角线上block进行转置时,我们读入了A[ii:ii+bsize][jj:jj+bsize]和B[jj:jj+bsize][ii:ii+bsize]所包含的共16个row sliver,都是不会发生冲突的。所以能看到的是一路hit,非常舒服……但是,在对对角线上block进行转置时,事情就没有那么顺利了。当i和j相等时,在这一步中:
B[j][i] = A[i][j];
由于A[i][j]和B[j][i]共用同个set,在读取完A[i][j]后,其所在row sliver被逐出,替换为B[j][i]所在row sliver。进行完store操作后,++j,A[i][j]大概率还是要使用这个set(它和A[i][j-1]很可能在同个row sliver里),所以B[j][i]所在row sliver被逐出。这个过程中发生了两次miss eviction。原本照我们希望的,A[ii][jj:jj+bsize]一路读全是hit,但是在对角线处被某个B的元素打断了。为了不让其被打断,我们可以进行些许修改:
void trans(int M, int N, int A[N][M], int B[M][N]) {
int i, j, ii, jj, a0, a1, a2, a3, a4, a5, a6, a7;
int bsize = 8;
for (jj = 0; jj < M; jj += bsize) {
for (ii = 0; ii < N; ii += bsize) {
for (i = ii; i < ii + bsize; ++i) {
j = jj;
a0 = A[i][j];
a1 = A[i][j + 1];
a2 = A[i][j + 2];
a3 = A[i][j + 3];
a4 = A[i][j + 4];
a5 = A[i][j + 5];
a6 = A[i][j + 6];
a7 = A[i][j + 7];
B[j][i] = a0;
B[j + 1][i] = a1;
B[j + 2][i] = a2;
B[j + 3][i] = a3;
B[j + 4][i] = a4;
B[j + 5][i] = a5;
B[j + 6][i] = a6;
B[j + 7][i] = a7;
}
}
}
}
我们把A[ii][jj:jj+bsize]先全部读完,放在临时变量里,然后再通过临时变量赋值给B中对应的元素。再读完A[ii][jj:jj+bsize]以后,它也就不需要继续存在于cache上了,即使被逐出也没有关系。粗略估计,这样做能减少一次miss eviction。在进行这种修改后,miss数减少到了287,达到了满分水平。不过,这个写法明显就不优雅。我在浏览GitHub它人答案后,发现了一个好得多的答案,如下:
void trans(int M, int N, int A[N][M], int B[M][N]) {
int i, j, ii, jj;
int bsize = 8;
for (jj = 0; jj < M; jj += bsize) {
for (ii = 0; ii < N; ii += bsize) {
for (j = jj; j < jj + bsize; ++j) {
for (i = ii + j - jj; i >= ii; --i) {
B[j][i] = A[i][j];
}
for (i = ii + j - jj + 1; i < ii + bsize; ++i) {
B[j][i] = A[i][j];
}
}
}
}
}
它做了两个重要的修改:
- 最内层循环从对
j循环,改成了对i循环。 - 从对角线位置开始赋值。先将对角线起到block上边界的那些
A元素转置了,再将对角线起到block下边界的那些A元素转置。
为了方便理解,在对处于对角线的block A[ii:ii+bsize][jj:jj+bsize]和B[jj:jj+bsize][ii:ii+bsize]转置时,假设A子矩阵的8个row sliver都在cache中。首先取出对角线元素A[i][i],hit,然后赋值给B[i][i],发生了miss eviction,并将B[j][i]所在row sliver读入cache中。在全部赋值完B[j][i]所在row sliver之前,都不会再发生其他miss eviction了。这么做也能减少一次miss eviction。(当然,这里为了清楚表达意思,做了一些省略。在对A[i][i]至block上边界元素遍历时,也会发生一次miss eviction。但这次miss eviction属于不可避免的miss,在之前的方法里也会有。如果想要细究,可以查看trace.f0记录)
64 * 64
矩阵扩大到了64 * 64,矩阵每一行有8个row sliver,所以矩阵4行就会占用完所有set。如果还是令bsize = 8,每个block的上下两部分(上4行和下4行)是不能同时存在于cache里的。在对这样的block进行转置时,必然会发生诸多miss eviction。经测试,bsize = 8时miss数为4419。我们简单地把bsize缩小为4,令整个block都能存在于cache内,这时miss数下降为1699,接近< 1300的满分要求。
64 * 64有一个更好的解法,但不是我想出来的。我参考了上面提到的那个答案,他是这样做的(我修改了他的符号以方便看懂):
void trans(int M, int N, int A[N][M], int B[M][N]) {
int a0, a1, a2, a3, a4, a5, a6, a7, i, j, ii, jj;
int bsize = 8;
for (jj = 0; jj < M; jj += bsize) {
for (ii = 0; ii < N; ii += bsize) {
for (i = ii; i < ii + 4; ++i) {
// 1 miss
a0 = A[i][jj];
a1 = A[i][jj + 1];
a2 = A[i][jj + 2];
a3 = A[i][jj + 3];
a4 = A[i][jj + 4];
a5 = A[i][jj + 5];
a6 = A[i][jj + 6];
a7 = A[i][jj + 7];
// 1 * 4 misses
B[jj][i] = a0;
B[jj + 1][i] = a1;
B[jj + 2][i] = a2;
B[jj + 3][i] = a3;
B[jj][i + 4] = a4;
B[jj + 1][i + 4] = a5;
B[jj + 2][i + 4] = a6;
B[jj + 3][i + 4] = a7;
}
for (j = jj; j < jj + 4; ++j) {
// 0 miss
a0 = B[j][ii + 4];
a1 = B[j][ii + 5];
a2 = B[j][ii + 6];
a3 = B[j][ii + 7];
// 2 + 1 * 3 misses
B[j][ii + 4] = A[ii + 4][j];
B[j][ii + 5] = A[ii + 5][j];
B[j][ii + 6] = A[ii + 6][j];
B[j][ii + 7] = A[ii + 7][j];
// 1 miss
B[j + 4][ii] = a0;
B[j + 4][ii + 1] = a1;
B[j + 4][ii + 2] = a2;
B[j + 4][ii + 3] = a3;
// 2 + 1 * 3 misses
B[j + 4][ii + 4] = A[ii + 4][j + 4];
B[j + 4][ii + 5] = A[ii + 5][j + 4];
B[j + 4][ii + 6] = A[ii + 6][j + 4];
B[j + 4][ii + 7] = A[ii + 7][j + 4];
}
}
}
}
他使用了bsize = 8的block。在每次取出一个row sliver A[ii][jj:jj+bsize]以后,将前半部分(4个元素)放在B中对应位置,另外4个放在同一行右偏4的位置上,如下图:
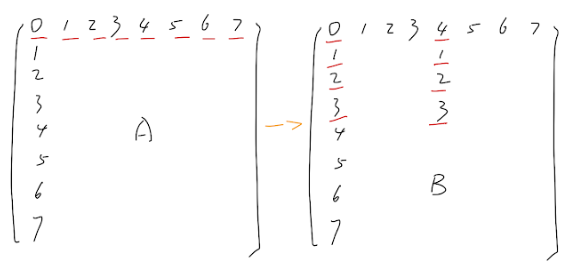
在存放后4个元素时不需要读入新的row sliver。在将A[ii:ii+bsize][jj:jj+bsize]前4行转移完后,再将B[jj:jj+bsize][ii:ii+bsize]的右上小块(4 * 4)保存到临时变量中,然后对右上小块求正确的转置值,然后将临时变量值转移到左下小块中,最后对右下小块求正确的转置值。我粗略估计了一下在对角线上,这种算法的miss eviction数,写在了代码注释中。可以看到,这段代码的编排巧妙地避免了许多miss,是花费了相当心思的精细作品。
61 * 67
这个是不规则的矩阵,只需要在分block时判断是否走到了边界就可以了。使用最简单的blocking方法就能通过,如下:
void trans(int M, int N, int A[N][M], int B[M][N]) {
int i, j, ii, jj;
int bsize = 8;
for (jj = 0; jj < M; jj += bsize) {
for (ii = 0; ii < N; ii += bsize) {
for (i = ii; (i < ii + bsize) && (i < N); ++i) {
for (j = jj; (j < jj + bsize) && (j < M); ++j) {
B[j][i] = A[i][j];
}
}
}
}
}
当bsize = 8时miss数是1913,当bsize = 16时miss数是1816,都能达到< 2000的满分条件。这可能是因为2000这个数值太高了,毕竟64 * 64需要达到1300。
总结
这是一个非常实用的实验。不过我觉得,要我写的话,我优化到blocking这里就不会再做下去了。找到一个合适的bsize效果已经足够好了,继续优化会让代码难以理解。不过这不代表我不需要懂得这些东西^_^。