01-二维数组查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
这道题我一开始用了复杂且低效的做法做(不好意思贴出来了),看了这位大神的解释后才恍然大悟。这道题的算法复杂度可以降低到O(m+n)(分别是二维数组的长和宽)。通过观察下面的图:
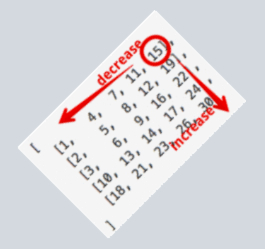
可以发现,如果我们从二维数组右上角的点开始,设当前点为array[x][y],如果array[x][y] < target,那么array[x][:y]这些元素,都会小于target。我们可以将当前点移动到array[x+1][y]表示将这部分元素舍弃。如果array[x][y] > target,则array[x+1:][y]的元素都会大于target。同理,我们将当前点移动到array[x][y-1],表示将这些元素舍弃。如果当前点走到了边界,依然没有碰到一个点是等于target的,说明二维数组里没有元素和target相等。
def Find(self, target, array):
x, y = 0, len(array[0]) - 1
while x < len(array) and y >= 0:
if array[x][y] == target:
return True
elif array[x][y] < target:
x += 1
else:
y -= 1
return False
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
if (array.size() == 0 || array[0].size() == 0)
return false;
int height = array.size(), width = array[0].size();
int x = 0, y = width - 1;
while (x < height && y >= 0) {
if (array[x][y] == target)
return true;
else if (array[x][y] > target)
--y;
else
++x;
}
return false;
}
};
06-旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
首先先写一个binary search回忆一下:
def binary_search(self, arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
在这道题里,也可以用binary search来找到数组的最小值。首先设left = 0, right = len(arr) - 1,在每个迭代中,从arr[left: right+1]中找出数组最小值的位置。left和right的中点mid所处的地方会有以下图中两种可能:
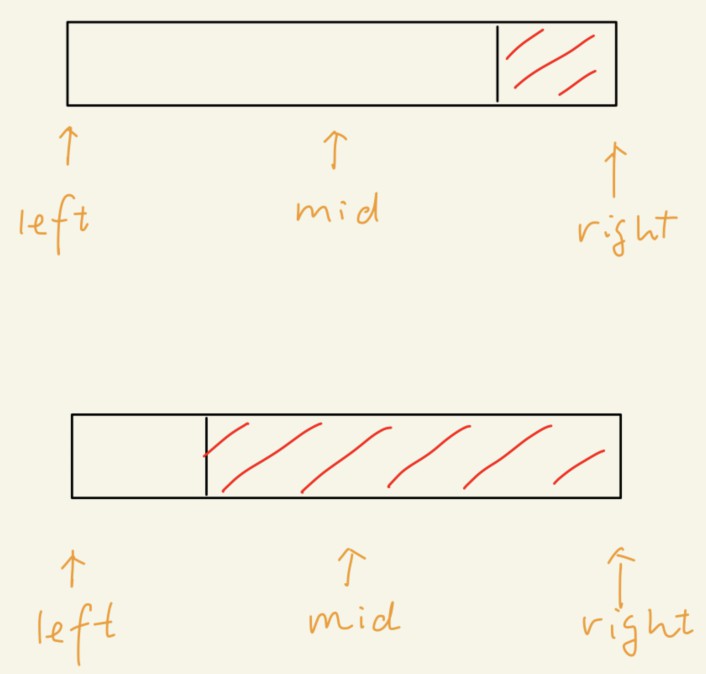
其中红色段是被旋转的部分。在第一种情况中,mid位于旋转数组的左边,那么要找的数组最小值(红色段头部)在mid的右边,可以让left = mid + 1继续寻找。在第二种情况中,mid位于旋转数组中,数组最小值在mid左边(或在mid的位置上),那么可以让right = mid继续寻找。
if arr[mid] > arr[right]: # 位于旋转数组左边
left = mid + 1
else: # 位于旋转数组中
right = mid
通过观察这个代码片段可以发现,mid始终位于[left, right]中,并且left和right终将走到一块。并且,它们的终点就是数组最小值的位置。因此,
def minNumberInRotateArray(self, nums):
if not nums:
return 0
left, right = 0, len(nums) - 1
while left < right:
mid = (left + right) // 2
if nums[right] < nums[mid]:
left = mid + 1
else:
right = mid
# 可以增加提前终止的条件。如果当前left/right已经到达数组最小值处的话,提前返回
# if right > 0 and nums[right-1] > nums[right]:
# return nums[right]
# if left > 0 and nums[left-1] > nums[left]:
# return nums[left]
return nums[left]
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.size() == 0)
return 0;
int left = 0, right = rotateArray.size() -1, mid;
while (left < right) {
mid = (left + right) / 2;
if (rotateArray[mid] < rotateArray[right])
right = mid;
else
left = mid + 1;
}
return rotateArray[left];
}
};
写binary search最大的难点就是边界问题。处理边界问题时,一定要有一以贯之的前提假设。在我的写法里,预先的假设就是,binary_search(arr, left, right, target)这个函数在arr[left: right+1]中找到target。如果arr[mid] < target,说明arr[left: mid+1]都不可能了,因此left = mid + 1。同理,arr[mid] > target时,arr[mid: right+1]都不可能,于是right = mid - 1。每一次迭代,都是根据更新后的left,right在arr[left: right+1]上寻找target。如果left > right,那么arr[left: right+1]将不包含元素,意味着数组上的元素都已被排除,没有元素等于target。在迭代结束后,left的位置应该是第一个比target大的元素的位置。
37-数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数。
这题一开始我是用binary search找到目标数字后,再线性地查看左右两边有多少个目标数字。这种方法不是很好,在某些情况下时间复杂度会下降到O(n)。下面是另一种更好的方法。由于binary search在迭代结束后,如果不返回mid(即找到目标),left所指的位置会是数组中第一个比target大的元素。因此,可以二分查找target+0.5和target-0.5,即第一个比target大的数的位置,和第一个target的位置(如果数组包含target的话。如果不包含,则是第一个大于target的数的位置,和target+0.5的搜索结果一样)。这两个结果相减,即夹在这两个数之间的长度,即target在数组中的数量。
class Solution:
def binary_search(self, arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
def GetNumberOfK(self, data, target):
return self.binary_search(data, target+0.5) - self.binary_search(data, target-0.5)
class Solution {
int BinarySearch(const vector<int> &data, double target) {
int left = 0, right = data.size() - 1, mid;
while (left <= right) {
mid = (left + right) / 2;
if (data[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return left;
}
public:
int GetNumberOfK(vector<int> data ,int k) {
return BinarySearch(data, k+0.5) - BinarySearch(data, k-0.5);
}
};