08-跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
超级简单的动态规划问题。设dp[i]为跳上第i级的跳法。那么有:
dp[i] = dp[i-1] + dp[i-2]。
讨论区说是斐波那契数列,确实是。不过斐波那契数列可以看作动态规划的一个特例,用斐波那契数列来想可能能减小空间复杂度(虽然通过动态规划优化也可以)。
def jumpFloor(self, number):
dp = [0] * (number+1)
dp[0], dp[1] = 1, 1
for i in range(2, number+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[-1]
class Solution {
public:
int jumpFloor(int number) {
int dp[number+1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= number; ++i) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[number];
}
};
09-变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
这题是上一题的延伸。既然青蛙可以跳任意级台阶,那么dp[i]就变成了:
dp[i] = dp[0] + dp[1] + ... + dp[i-1]。
def jumpFloorII(self, number):
dp = [0] * (number+1)
dp[0], dp[1] = 1, 1
for i in range(2, number+1):
dp[i] = sum(dp[:i])
return dp[-1]
不过,由于
dp[i-1] = dp[0] + dp[1] + ... + dp[i-2] = dp[i] - dp[i-1],
所以dp[i] = 2 * dp[i-1],可以免去求和步骤。
def jumpFloorII(self, number):
dp = [0] * (number+1)
dp[0], dp[1] = 1, 1
for i in range(2, number+1):
dp[i] = 2 * dp[i-1]
return dp[-1]
class Solution {
public:
int jumpFloorII(int number) {
int dp[number+1];
dp[1] = 1;
for (int i = 2; i <= number; ++i) {
dp[i] = dp[i-1] * 2;
}
return dp[number];
}
};
10-矩形覆盖
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
这题的代码跟青蛙跳台阶那一题是完全一样的。但是这题比较难想。设dp[i]为覆盖一个2*i的大矩形的方法数。我们已经知道了dp[1], dp[2], ..., dp[n-1],在覆盖2*n矩形时,可以有两种选择:
- 用一块竖着的矩形插到最右一列上。这种方式的覆盖方法有
dp[n-1]种。 - 用两块横着的矩形去覆盖
n-1, n两列。这种方式的覆盖方法有dp[n-2]种。
因此,
dp[i] = dp[i-1] + dp[i-2]。
def rectCover(self, number):
if number == 0:
return 0
dp = [0] * (number+1)
dp[0], dp[1] = 1, 1
for i in range(2, number+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[-1]
class Solution {
public:
int rectCover(int number) {
if (number == 0) return 0;
int dp_0 = 1, dp_1 = 1, dp_i = 1;
for (int i = 2; i <= number; ++i) {
dp_i = dp_0 + dp_1;
dp_0 = dp_1, dp_1 = dp_i;
}
return dp_i;
}
};
14-剪绳子
给你一根长度为n的绳子,请把绳子剪成m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]*k[1]*…*k[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
这道题最直接的方法是动态规划。设dp[i]是剪长度为i的绳子可以得到的最大乘积。注意这里可以剪成一段或多段。由于题目要求剪成多段,所以只要特别处理一下dp[number]就可以了。时间复杂度为O(n^2)。这道题有其他巧妙的方法,通过找规律,可以发现一种复杂度为O(lgn)的方法。有兴趣可以看牛客网讨论区,这个方法并不是很泛用。
class Solution:
def cutRope(self, number):
dp = [1 for _ in range(number+1)]
for i in range(2, number):
dp[i] = max([dp[i-j] * j for j in range(1, i+1)])
return max([dp[number-j] * j for j in range(1, number)])
class Solution {
public:
int cutRope(int number) {
int dp[number+1];
int tmp;
dp[1] = 1, dp[2] = 1;
for (int i = 3; i <= number; ++i) {
dp[i] = 1;
for (int j = 2; j < i; ++j) {
tmp = (dp[i-j] >= (i-j) ? dp[i-j] : (i-j)) * j;
if (tmp > dp[i]) dp[i] = tmp;
}
}
return dp[number];
}
};
30-连续子数组的最大和
给一个数组,返回它的最大连续子序列的和。例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。
删掉了题目前面半段莫名其妙的话。仍记得这题是本科学校ACM俱乐部宣讲会上介绍的问题,当时我没想出来(当时就是个弟弟)。这题可以用动态规划想,也可以用贪心算法的思路想。设dp[i]是以array[i]结尾的最大连续子序列的和。那么,在已知dp[i-1]后,如果dp[i-1] <= 0,那么以array[i]结尾的连续子序列不要dp[i-1]对应的子序列也罢,因为它只有反效果(和变小了,还不如序列中只有一个array[i]。因此,
dp[i] = dp[i-1] + array[i] if dp[i-1] > 0 else array[i]。
在计算动态规划的递推式时,其实已经用贪心算法的思维在思考了。把动态规划的代码优化一下(用两个变量来存储dp[i-1]和dp[i]),就变得更像是贪心算法了。殊途同归。
def FindGreatestSumOfSubArray(self, array):
dp = [0] * len(array)
dp[0] = array[0]
for i in range(1, len(array)):
dp[i] = dp[i-1] + array[i] if dp[i-1] > 0 else array[i]
return max(dp)
// 优化了一下,不需要数组
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int max = 0x80000000, dp = 0;
for (int &each: array) {
if (dp > 0) dp += each;
else dp = each;
if (max < dp) max = dp;
}
return max;
}
};
33-丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
这道题我曾经在ugly-numbers见到过,并且写了一个英文的笔记。这里就直接贴出来了。
Ugly numbers are numbers whose only prime factors are 2, 3 or 5. The sequence 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, … shows the first 11 ugly numbers. By convention, 1 is included. Given a number n, the task is to find n’th Ugly number.
This is a basic dynamic programming problem. The key is: after we get a list of ugly numbers, we can get more by multiply 2, 3, or 5 with every ugly numbers we have. Therefore, the smallest ugly number we haven’t gotten would be generated by multiplying 2, 3 or 5 with the smallest ugly number we haven’t dealt with.
Given the list of already gotten ugly numbers:
ugly = [1, 2, 3, 4, 5]
And we set i2, i3, i5= 0, 0, 0 to point elements in the ugly array, in which i2 points to the ugly number that: 1) ugly[i2] * 2 is still not in ugly; 2) for each i that ugly[i] * 2 is not in ugly, we have ugly[i2] <= ugly[i]. In a similar way, i3 and i5 are the smallest number that could be used to get a new ugly number by multiplying 3 or 5. We can easily know that the smallest unseen ugly number is between: ugly[i2] * 2, ugly[i3] * 3 and ugly[i5] * 5.
def getNthUglyNo(n):
# initialize i2, i3 and i5
i2, i3, i5 = 0, 0, 0
# the first element of ugly number array is 1 by convention
ugly = [1]
for i in range(n-1):
ugly_i2 = ugly[i2] * 2
ugly_i3 = ugly[i3] * 3
ugly_i5 = ugly[i5] * 5
# the smallest number is between
min_new_ugly = min(ugly_i2, ugly_i3, ugly_i5)
# sometimes min_new_ugly is equal to ugly_i2 and ugly_i3 in the same time, for example.
# in this case, after appending min_new_ugly into the ugly array, both ugly_i2 and ugly_i3
# can not be used to get new ugly number any more, so move both i2 and i3 one step forward.
if min_new_ugly == ugly_i2:
# move i2 one step forward
i2 += 1
if min_new_ugly == ugly_i3:
i3 += 1
if min_new_ugly == ugly_i5:
i5 += 1
ugly.append(min_new_ugly)
return ugly[n-1]
class Solution {
public:
int GetUglyNumber_Solution(int index) {
if (index == 0) return 0;
int i2 = 0, i3 = 0, i5 = 0;
int t1, t2, t3, min = 1;
int ugly[index];
ugly[0] = 1;
for (int i = 1; i < index; ++i) {
t1 = ugly[i2] * 2, t2 = ugly[i3] * 3, t3 = ugly[i5] * 5;
min = t1 > t2 ? (t2 > t3 ? t3 : t2) : (t1 > t3 ? t3 : t1);
if (min == t1) ++i2;
if (min == t2) ++i3;
if (min == t3) ++i5;
ugly[i] = min;
}
return min;
}
};
46-孩子们的游戏-圆圈中最后剩下的数
每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0…m-1报数….这样下去….直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1)
如果没有小朋友,请返回-1
设dp[i]是当小朋友人数为i时,最终获得礼品的小朋友的编号。显然,dp[1] = 0。我们可以认为,在一个长度为i的环里,偏移为dp[i]的元素是我们想要的元素。而在长度为i+1的环里,偏移为m+dp[i]的元素是我们想要的(因为先偏移m淘汰一个小朋友,此时环就是一个长度i的环。从下一个位置开始,偏移dp[i]能找到最终胜利者)。
class Solution:
def LastRemaining_Solution(self, n, m):
if not n or not m:
return -1
idx = 0
for i in range(2, n+1):
idx = (m + idx) % i
return idx
class Solution {
public:
int LastRemaining_Solution(int n, int m) {
if (n <= 0 || m <= 0) return -1;
int idx = 0;
for (int i = 2; i <= n; ++i) {
idx = (m + idx) % i;
}
return idx;
}
};
52-正则表达式匹配
这题我曾经在LeetCode上做过,使用了状态机的方法。由于我个人很喜欢状态机的做法,所以下面贴出当时用状态机解答问题做的(英文)笔记:
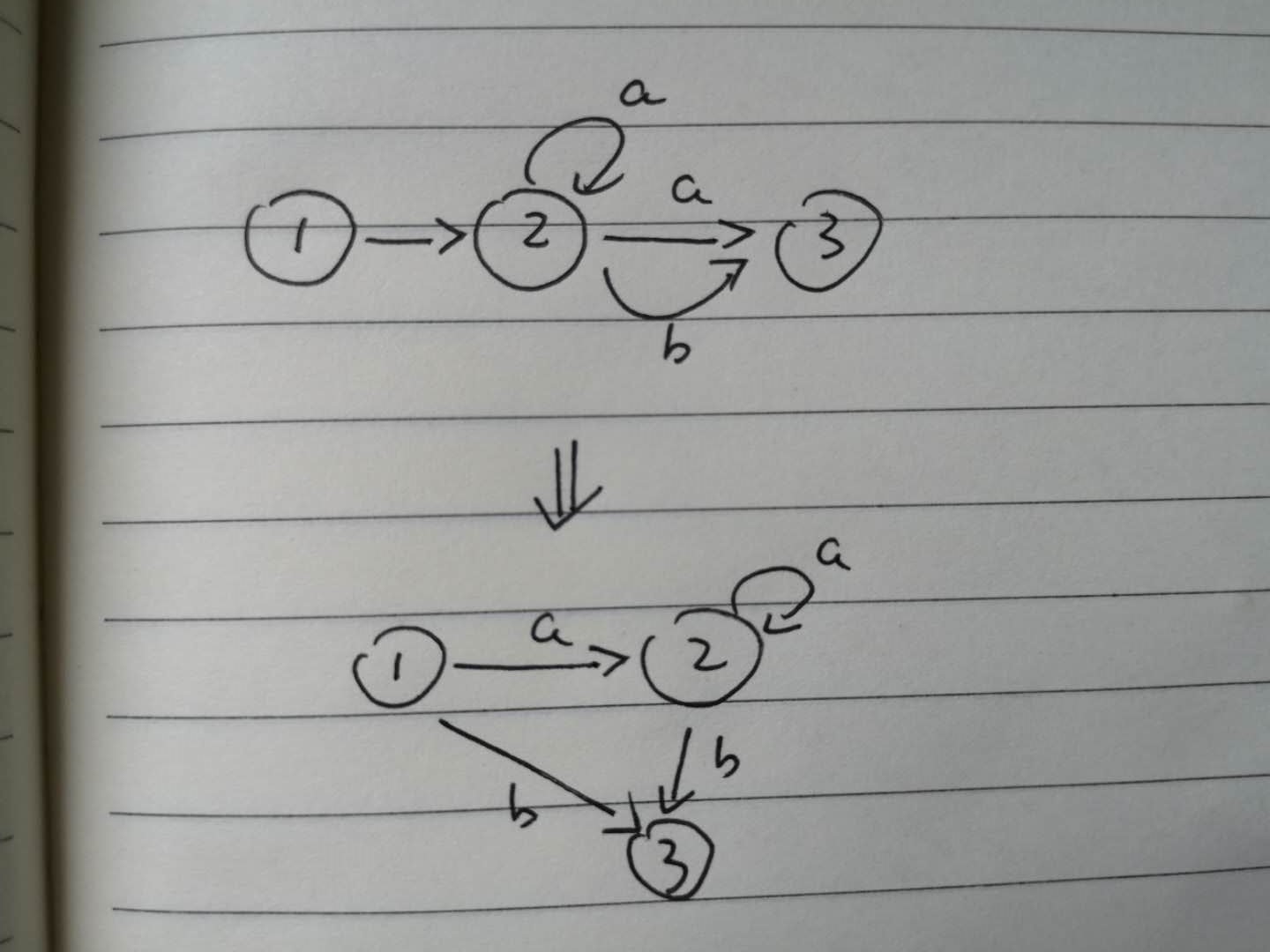
This version of my state machine is easy to understand. However, this is a NFA (Nondeterminism Finite Automaton). Without further optimazation, my code got Time Limit Exceeded when submitted to LeetCode. A good solution is to transform it to a DFA (Deterministic Finite Automation).
Here is a DFA written by cbmbbz:
from collections import defaultdict
class Solution:
def isMatch(self, s, p):
transfer = defaultdict(set)
curr_states = [0]
for i,c in enumerate(p):
if c=='*':
continue
# an id for new state
new_state = curr_states[-1] + 1
for state in curr_states:
transfer[state, c].add(new_state)
if i < len(p) - 1 and p[i + 1] == '*': # if next c is *
transfer[new_state, c] = {new_state}
curr_states.append(new_state)
else:
curr_states = [new_state]
success = curr_states # final states
curr_states = {0}
for c in s:
next_states = set()
for state in curr_states:
next_states.update(transfer[state, c] | transfer[state, '.'])
curr_states = next_states
return any(state in curr_states for state in success) # check any curr_states is success
动态规划的做法更为直观。设dp[i][j]为s[:i]和p[:j]是否匹配。如果匹配dp[i][j]则为True,否则为False。如果s[i] == p[j],那么一定是因为p[j]是一个字母,刚好与s[i]相同。这种情况下,如果s[:i]和p[:j]匹配上,那么s[:i+1]和p[:j+1]就能匹配上。即:
dp[i+1][j+1] = dp[i][j]。
如果s[i] != p[j],那么就要看p[j]是什么了。如果p[j]是一个字母,那么s[i]和p[j]就不可能匹配上了(因为结尾部分不一样)。因此,dp[i+1][j+1] = False。如果p[j]不是字母,而是通配符.,那么不管s[i]是什么都能匹配上,因此dp[i+1][j+1] = dp[i][j],只需要s[:i]和p[:j]匹配上就可以了。如果p[j]是*,那么有三种情况:
x*(x是p[j-1])不和s[:i+1]中的字母匹配。那么s[:i+1]和p[:j+1]要匹配上,必须要让s[:i+1]和p[:j-1]匹配上,因此dp[i+1][j+1] = dp[i+1][j-1]。x*和s[i]匹配,即只匹配一个字母。这种情况的前提是x == s[i]。满足前提后,如果s[:i]能和p[:j-1]匹配上的话,s[:i+1]和p[:j+1]就能匹配上。因此,dp[i+1][j+1] = dp[i][j-1]。x*和若干个s中的字母匹配。在这种情况下,如果s[:i+1]和p[:j+1]匹配上了,肯定有s[:i]也和p[:j+1]能匹配上,因为x*能和s尾部若干个(大于1个)字母匹配。因此,dp[i+1][j+1] = dp[i][j+1]。
综上,代码如下:
def isMatch(self, s: str, p: str) -> bool:
dp = [[False] * (len(p)+1) for _ in range(len(s)+1)]
# initialize
dp[0][0] = True
for j in range(1, len(p), 2):
if p[j] == '*':
dp[0][j+1] = True
else:
break
for i in range(len(s)):
for j in range(len(p)):
if s[i] == p[j] or p[j] == '.':
dp[i+1][j+1] = dp[i][j]
elif p[j] == '*':
case1, case2, case3 = False, False, False
if j > 0:
case1 = dp[i+1][j-1]
if p[j-1] == s[i] or p[j-1] == '.':
case2 = dp[i][j-1]
case3 = dp[i][j+1]
dp[i+1][j+1] = case1 or case2 or case3
# else:
# # s[i-1] != p[j-1]
# dp[i][j] = False
return dp[len(s)][len(p)]
class Solution {
public:
bool match(char* str, char* pattern) {
int len_s = 0, len_p = 0;
for (; str[len_s] != '\0'; ++len_s) ;
for (; pattern[len_p] != '\0'; ++len_p) ;
int dp[len_s+1][len_p+1];
for (int i = 0; i <= len_s; ++i)
for (int j = 0; j <= len_p; ++j)
dp[i][j] = 0;
dp[0][0] = 1;
for (int j = 1; j < len_p; j+=2) {
if (pattern[j] == '*') dp[0][j+1] = 1;
else break;
}
for (int i = 0; i < len_s; ++i) {
for (int j = 0; j < len_p; ++j) {
if (str[i] == pattern[j] || pattern[j] == '.')
dp[i+1][j+1] = dp[i][j];
else if (pattern[j] == '*') {
if (j > 0) {
dp[i+1][j+1] |= dp[i+1][j-1];
if (pattern[j-1] == str[i] || pattern[j-1] == '.') {
dp[i+1][j+1] |= dp[i][j-1];
dp[i+1][j+1] |= dp[i][j+1];
}
}
}
}
}
return dp[len_s][len_p];
}
};