617. Merge Two Binary Trees
Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.
Example 1:
Input: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 Output: Merged tree: 3 / \ 4 5 / \ \ 5 4 7
这道题可以递归地同时访问t1和t2。在它们的当前根节点都不为None时,新建一个节点,其值为两个根节点值的和;在某个根节点为None时,新建一个树,其为另一个根节点所属子树的拷贝(在我的代码中,我没有做这一步,因为偷懒了,而且时间会更快……但这是不对的);如果两个根节点都是None,则返回None。
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if not t1 and not t2:
return None
elif not t1:
return t2
elif not t2:
return t1
else:
node = TreeNode(t1.val + t2.val)
node.left = self.mergeTrees(t1.left, t2.left)
node.right = self.mergeTrees(t1.right, t2.right)
return node
338. Counting Bits
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.
Example 1:
Input: 2 Output: [0,1,1]Example 2:
Input: 5 Output: [0,1,1,2,1,2]
(1) DP方法:
一个数如果是奇数,那么它的二进制表示会比它右移一位的数的二进制表示多一个一;否则一的个数相等。
class Solution:
def countBits(self, num: int):
dp = [0 for _ in range(num+1)]
for i in range(1, num+1):
if i % 2 == 0:
dp[i] = dp[i//2]
else:
dp[i] = dp[i//2] + 1
return dp
(2) 找规律:
[2^n, 2^(n+1))的数字数目,等于[0:2^n)的数字数目(因为在[0:2^n)的每个数的二进制表示前面加一个1,就会变成[2^n, 2^(n+1))里的数)。因此,可以先求去一个最小的n,使得2^n>num,然后每次使用[0:2^i)中的数的1的个数,去求[2^i, 2^(i+1))中的数的1的个数(只需加一即可),并将结果添加至结果数组里。最后,取结果数组的前num+1项。
class Solution:
def countBits(self, num: int):
if num == 0:
return [0]
# find a n which is the smallest integer that 2^n >= num
n, tmp = -1, num
while tmp != 0:
n += 1
tmp >>= 1
ans = [0, 1]
# construct ans[:2^n]
while n > 0:
ans.extend([1+x for x in ans])
n -= 1
return ans[:num+1]
104. Maximum Depth of Binary Tree
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7return its depth = 3.
非常基础的递归。
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
这是DFS,或者也可以用层次遍历/BFS。因为所有节点都必须被访问一次,所以没有时间上的区别。
136. Single Number
Given a non-empty array of integers, every element appears twice except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
Example 1:
Input: [2,2,1]
Output: 1
Example 2:
Input: [4,1,2,1,2]
Output: 4
把全部数XOR起来,剩下的数就是the single one。这是因为相同的数异或为0,而0与其他数异或为其他数。
from functools import reduce
class Solution:
def singleNumber(self, nums: List[int]) -> int:
return reduce(lambda x, y: x^y, nums)
406. Queue Reconstruction by Height
Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers
(h, k), wherehis the height of the person andkis the number of people in front of this person who have a height greater than or equal toh. Write an algorithm to reconstruct the queue.Note: The number of people is less than 1,100.
Example
Input: [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] Output: [[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
一个比较矮的人无论是站在一个更高的人的前面或者后面,对他的k值都不会有影响。因此,可以考虑用插入的方式构造队列:先插入最高的人,然后插入第二高的,然后是第三高……直到插入了所有人。插入一个比较矮的人,对队列中已经存在的人的k是没有影响的。因此,只需要为这个比较矮的人寻找一个合适的位置,让他取到对的k值,就能让队列中已有的人的k值都是正确的。就像这样,不断插入拥有对的k值的人,最终排好的队列中的人的k值都会是对的。
class Solution:
def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
people.sort(key=lambda x: (-x[0], x[1]))
ans = []
for each in people:
ans.insert(each[1], each)
return ans
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>> &people) {
if (people.size() == 0) return {};
std::sort(
people.begin(), people.end(), [](vector<int> &x, vector<int> &y) {
return x[0] > y[0] || (x[0] == y[0] && x[1] < y[1]);
});
vector<vector<int>> rtn;
for (auto &p : people) {
rtn.insert(rtn.begin() + p[1], p);
}
return rtn;
}
};
739. Daily Temperatures
Given a list of daily temperatures
T, return a list such that, for each day in the input, tells you how many days you would have to wait until a warmer temperature. If there is no future day for which this is possible, put0instead.For example, given the list of temperatures
T = [73, 74, 75, 71, 69, 72, 76, 73], your output should be[1, 1, 4, 2, 1, 1, 0, 0].Note: The length of
temperatureswill be in the range[1, 30000]. Each temperature will be an integer in the range[30, 100].
这种求一个方向上的递增或递减的题,大部分可以用栈解决。使用一个栈stack,用来在访问完每个温度值后存入该温度值的索引。在访问一个新的温度值t时,如果它跟栈顶温度值索引对应的温度相比更大时,便进行pop,并在栈顶索引对应的输入数组位置上记录数值。简单地说,stack里留存的是那些还没有找到接下来的更暖气温的气温值索引。在它们找到了一个更暖的气温后,便从栈中弹出,并记录花费的天数。
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
stack = []
ans = [0 for _ in range(len(T))]
for i, t in enumerate(T):
while stack and T[stack[-1]] < t:
ans[stack[-1]] = i - stack[-1]
stack.pop()
stack.append(i)
return ans
226. Invert Binary Tree
Invert a binary tree.
Example:
Input:
4 / \ 2 7 / \ / \ 1 3 6 9Output:
4 / \ 7 2 / \ / \ 9 6 3 1
传说中Homebrew作者面试谷歌时做不出而导致被挂的题……其实很简单嘛,可能是一时忘了二叉树的结构?……感觉这道题在递归之中确实是偏简单,把当前访问节点的左右节点互换,然后递归地处理左右子树就行了。
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
94. Binary Tree Inorder Traversal
Given a binary tree, return the inorder traversal of its nodes’ values.
Example:
Input: [1,null,2,3] 1 \ 2 / 3 Output: [1,3,2]
参见另一个页面。
46. Permutations
Given a collection of distinct integers, return all possible permutations.
Example:
Input: [1,2,3] Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
这道题最符合直觉的做法就是递归。假设通过递归,获得了nums[1:]的所有置换后,要获得nums的置换,只需要将nums[0]插入到nums[1:]的置换的各个位置上即可。或者也可以换种思路:依次取nums中的一个元素nums[i],计算剩下元素nums[:i]+nums[i+1:]的所有置换。然后在这些置换的最前添加nums[i](也就是计算所有以nums[i]开头的置换)。这两种方法简单地想,应该有差不多的复杂度(不过在LeetCode的测试用例上第一种会省时一点。但是算法复杂度应该是一样的)
class Solution:
def permute(self, nums: 'List[int]') -> 'List[List[int]]':
if len(nums) <= 1:
return [nums]
pers = self.permute(nums[1:])
ans = []
for each in pers:
for i in range(len(each)+1):
ans.append(each[:i] + [nums[0]] + each[i:])
return ans
class Solution:
def permute(self, nums: 'List[int]') -> 'List[List[int]]':
if len(nums) <= 1:
return [nums]
ans = []
for i in range(len(nums)):
pers = self.permute(nums[:i] + nums[i+1:])
ans.extend([[nums[i]] + each for each in pers])
return ans
class Solution {
vector<vector<int>> rtn;
void recursive(vector<int> &nums, int start, int end) {
if (start == end) {
rtn.push_back(nums);
return;
}
for (int i = start; i <= end; ++i) {
swap(nums[start], nums[i]);
recursive(nums, start + 1, end);
swap(nums[start], nums[i]);
}
}
public:
vector<vector<int>> permute(vector<int>& nums) {
rtn.clear();
recursive(nums, 0, nums.size()-1);
return rtn;
}
};
下面是Permutations II,nums中会有重复,结果需要去重。做法的思路是一样的,只是需要先对nums进行排序,在碰到重复元素时跳过即可。
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
if len(nums) <= 1:
return [nums]
ans = []
nums.sort()
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i-1]:
continue
pers = self.permuteUnique(nums[:i] + nums[i+1:])
ans.extend([[nums[i]] + each for each in pers])
return ans
647. Palindromic Substrings
Given a string, your task is to count how many palindromic substrings in this string.
The substrings with different start indexes or end indexes are counted as different substrings even they consist of same characters.
Example 1:
Input: "abc" Output: 3 Explanation: Three palindromic strings: "a", "b", "c".Example 2:
Input: "aaa" Output: 6 Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
这道题我已知的有两种做法。第一种是我用的DP方法。令dp[i][j]表示子串s[i:j+1]是否为回文。对于所有i,肯定有dp[i][i] = 1。然后依次计算s的长度为length的子串是否回文。如果s[i+1:i+length-1]是回文,且s[i] == s[i+length],那么s[i:i+length+1]也会是回文。这种做法的时间复杂度是O(n^2)。不过这种方法不如下面一种方法。下面的方法在s[i:j]不为回文的情况下,就不会再计算s[i-1:j+1]、s[i-2:j+2]……了,在效率上更佳。
class Solution:
def countSubstrings(self, s: str) -> int:
if not s:
return 0
# dp[i][j] = num of palindromic substrings in s[i:j+1]
dp = [[0 for _ in s] for _ in s]
for i in range(len(s)):
dp[i][i] = 1
for length in range(1, len(s)):
for i in range(len(s)):
end = i + length
if end >= len(s):
continue
if s[i] == s[end] and (length == 1 or dp[i+1][end-1]):
dp[i][end] = 1
return sum([sum(each) for each in dp])
class Solution:
def countSubstrings(self, s: str) -> int:
if not s:
return 0
self.count = 0
def extend(left, right):
while left >= 0 and right < len(s) and s[left] == s[right]:
self.count += 1
left, right = left - 1, right + 1
for i in range(len(s)):
extend(i, i)
extend(i, i + 1)
return self.count
22. Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]
这是一个非常简单的回溯问题。在回溯过程中,保持以下规律:
- 每添加一个”(“,就必须添加一个”)”
- ”(“的总数为
n - “)”的个数在子串
s[:i]中不能比”(“的个数多
就可以筛选掉那些不符合要求的置换。
class Solution:
def generateParenthesis(self, n: int) -> 'List[str]':
if n == 0:
return []
ans = []
def recursive(left, right, s):
if left == 0 and right == 0:
ans.append(s)
if left > 0:
recursive(left - 1, right + 1, s + '(')
if right > 0:
recursive(left, right - 1, s + ')')
recursive(n, 0, '')
return ans
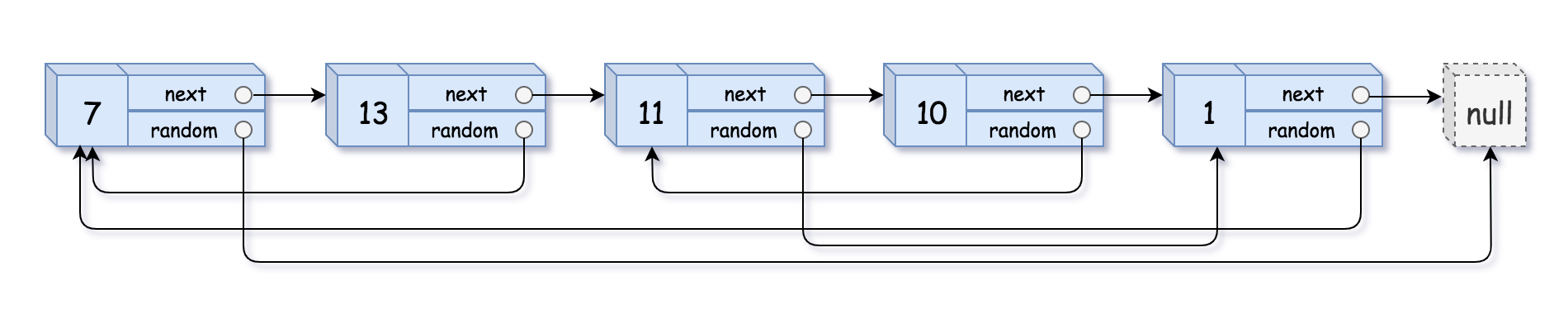
206. Reverse Linked List
Reverse a singly linked list.
Example:
Input: 1->2->3->4->5->NULL Output: 5->4->3->2->1->NULL
这道题非常经典……见了无数次。首先是递归版本。递归地将当前头部的下个节点为头部的链表翻转。然后翻转链表的尾部——即当前头部的下一个节点——的next设为头部,而头部的next设为None即可。另外,递归还可以像这样,在递归过程中按顺序翻转节点间的指向(从头到尾,而我的是从尾到头)。
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head or not head.next:
return head
new_head = self.reverseList(head.next)
head.next.next = head
head.next = None
return new_head
迭代版本使用3个指针prev,cur和nex来分别指向当前节点的前一个节点、当前节点、当前节点下一个节点。在迭代过程中,将cur.next设为prev,然后三个指针分别向前移动一个节点(nex的意义是为了防止改变cur.next后无法到达原链表中当前节点的下一个节点)。
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if not head or not head.next:
return head
prev, cur, nex = None, head, head.next
while nex:
cur.next = prev
prev, cur, nex = cur, nex, nex.next
cur.next = prev
return cur
347. Top K Frequent Elements
Given a non-empty array of integers, return the k most frequent elements.
Example 1:
Input: nums = [1,1,1,2,2,3], k = 2 Output: [1,2]Example 2:
Input: nums = [1], k = 1 Output: [1]
如果用Counter来计算频率的话,那代码就太简单了。在排序频率时可以优化。因为所有数的频率的范围在[1, len(nums)]之间,所以可以用桶bucket[i]来装频率为i的所有数。这样算法复杂度可以降到O(n)。不过可能是桶使用列表来装数,不如builtin函数高效,用桶的实现甚至比下面的代码还慢。
from collections import Counter
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
ctr = Counter(nums)
return [x[0] for x in sorted(ctr.items(), key=lambda x: -x[1])[:k]]
238. Product of Array Except Self
Given an array
numsof n integers where n > 1, return an arrayoutputsuch thatoutput[i]is equal to the product of all the elements ofnumsexceptnums[i].Example:
Input: [1,2,3,4] Output: [24,12,8,6]
题目的意思是,ans[i]是nums[:i] + nums[i+1:]中元素的累乘。因此,可以从左到右线性地算出各个nums[:i]的累乘,再从右到左算出各个nums[i+1:]的累乘。然后,ans[i]等于对应位置的左右累乘的积。这样算法复杂度就为O(n)。下面的做法用了两个数组记录左右累乘,来回共遍历了3趟。这个做法把计算从右到左累乘和计算结果两步合在一起了,并且少用一个数组,大有可借鉴之处。
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left, right = [1 for _ in nums], [1 for _ in nums]
for i in range(1, len(nums)):
left[i] = left[i-1] * nums[i-1]
for i in range(len(nums)-2, -1, -1):
right[i] = right[i+1] * nums[i+1]
for i in range(len(nums)):
left[i] = left[i] * right[i]
return left
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left, right = [1 for _ in nums], 1
for i in range(1, len(nums)):
left[i] = left[i-1] * nums[i-1]
for i in range(len(nums)-1, -1, -1):
left[i] = left[i] * right
right = right * nums[i]
return left
78. Subsets
Given a set of distinct integers,
nums, return all possible subsets (the power set).Note: The solution set must not contain duplicate subsets.
Example:
Input: nums = [1,2,3] Output: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
这题是典型的回溯。关于回溯,讨论区有个人总结了一些LeetCode上的回溯题。我下面的做法比较符合直觉,不过也可以像链接中那样,用循环代替一层递归,这样可能会比较省空间。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans = []
def recursive(arr, i):
if i >= len(nums):
ans.append(arr.copy())
else:
arr.append(nums[i])
recursive(arr, i+1)
arr.pop()
recursive(arr, i+1)
recursive([], 0)
return ans
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans = []
def recursive(arr, i):
ans.append(arr.copy())
for j in range(i, len(nums)):
arr.append(nums[j])
recursive(arr, j+1)
arr.pop()
recursive([], 0)
return ans
下面是Subsets II,nums中的元素会重复,要求要去重。思路是一样的,只是回溯时需要跳过重复的元素。
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
ans = []
nums.sort()
def recursive(arr, i):
ans.append(arr.copy())
for j in range(i, len(nums)):
if j > i and nums[j] == nums[j-1]:
continue
arr.append(nums[j])
recursive(arr, j+1)
arr.pop()
recursive([], 0)
return ans
283. Move Zeroes
Given an array
nums, write a function to move all0’s to the end of it while maintaining the relative order of the non-zero elements.Example:
Input: [0,1,0,3,12] Output: [1,3,12,0,0]
使用一个指针i,nums[:i]都是非0的数,且保留了原来的顺序。然后遍历nums,每发现一个非0的数,就跟nums[i]调换,并且让i加一。这道题的思路跟low, high指针(或者left, right指针)操作一个线性数组的题目是一样的。
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
i = 0
for j, num in enumerate(nums):
if num != 0:
nums[i], nums[j] = nums[j], nums[i]
i += 1
169. Majority Element
Given an array of size n, find the majority element. The majority element is the element that appears more than
⌊ n/2 ⌋times.You may assume that the array is non-empty and the majority element always exist in the array.
Example 1:
Input: [3,2,3] Output: 3Example 2:
Input: [2,2,1,1,1,2,2] Output: 2
这道题的解法,是一种叫Boyer–Moore majority vote algorithm的算法。附带一个这个算法的证明。
在起始时,将nums[0]当做majority element(me)。count的意义是“在已经访问的元素中,当前me的数目比不是me的数目多的个数”。故起始时count为1。顺序访问数组,如果访问到的数等于当前me,则++count;否则--count。
可以用数学归纳法证明。如果nums.size() == 1,显然返回的元素(第一个元素)是正确答案。
设nums.size()在[1, n-1]以内时返回的元素是正确答案。
如果count == 0,说明目前已访问的元素中,没有一个的个数比其他的总数大。设已经访问了x个元素,则全局me在这x个元素中至多出现了x/2次。由于me的个数大于n/2,所以在剩下的n-x个元素中,它至少会出现(n-x)/2+1次,即它在剩下的n-x个元素中依然是me。那么对剩下的n-x个元素递归地调用函数majorityElement,由于n-x属于[1, n-1],返回的元素是n-x的me,即是全局me。
代码实现不必使用递归,用迭代代替就可以了。
class Solution:
def majorityElement(self, nums: List[int]) -> int:
count = 1
ans = nums[0]
for num in nums[1:]:
if count == 0:
ans = num
count = 1
else:
if ans != num:
count -= 1
else:
count += 1
return ans
448. Find All Numbers Disappeared in an Array
Given an array of integers where
1 ≤ a[i] ≤ n(n= size of array), some elements appear twice and others appear once.Find all the elements of [1, n] inclusive that do not appear in this array.
Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.
Example:
Input: [4,3,2,7,8,2,3,1] Output: [5,6]
这道题的技巧是用已有的空间,去记录计算结果。由于数组元素的取值在[1, n]之间,且数组的大小也是n,刚好可以用原数组来记录哪些值不在数组里。遍历数组,每发现一个新的值n,就将nums[n-1]这个元素取反。这样,数组中为负数的元素对应的下标,就会是那些出现过在数组中的数了。
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
idx = abs(nums[i]) - 1
if nums[idx] > 0:
nums[idx] = -nums[idx]
return [i+1 for i in range(len(nums)) if nums[i] > 0]
49. Group Anagrams
Given an array of strings, group anagrams together.
Example:
Input: ["eat", "tea", "tan", "ate", "nat", "bat"], Output: [ ["ate","eat","tea"], ["nat","tan"], ["bat"] ]
所谓的anagrams即是改变单词中字母顺序后,能够相等的两个单词。可以让每个单词的字母排序,anagrams的排序结果是相同的。也可以为每个单词计算一个26元素的数组arr,arr[i]表示第i个字母出现的次数。anagrams的arr也是相同的。这里可以直接把arr转换成一个字符串,比较anagrams时更为快捷。具体做法是对每个出现过的字母,将这个字母和它的频数一起添加进单词的arr字符串中。
其实将arr转换成字符串,可以看做一种哈希方法,将单词中出现的字母和它们的频数哈希成一个方便比较的指纹,然后和其他单词的指纹比较。我之前看过另一种哈希方法,就是让每个字母对应一个质数,然后将单词中所有字母对应的质数的乘积作为指纹。这样包含相同字母+字母频数的单词的指纹值时相同的单词是anagrams。不过这种做法容易让指纹值溢出。现在LeetCode好像会对溢出报错,所以这种哈希方法难以实行了。但是它的效率绝对会比我用的方法快很多。
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string> &strs) {
if (strs.empty()) return {};
map<string, vector<string>> m;
for (string str : strs) {
char arr[26] = {0};
for (char c : str) ++arr[c - 'a'];
string arr_s;
for (int i = 0; i < 26; ++i) arr_s += (char)('a' + i) + to_string(arr[i]);
if (m.find(arr_s) == m.end()) m[arr_s] = {};
m[arr_s].push_back(str);
}
vector<vector<string>> rtn;
for (map<string, vector<string>>::iterator it = m.begin();
it != m.end(); ++it)
rtn.push_back(it->second);
return rtn;
}
};
39. Combination Sum
Given a set of candidate numbers (
candidates) (without duplicates) and a target number (target), find all unique combinations incandidateswhere the candidate numbers sums totarget.The same repeated number may be chosen from
candidatesunlimited number of times.Note:
- All numbers (including
target) will be positive integers.- The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [2,3,6,7], target = 7, A solution set is: [ [7], [2,2,3] ]Example 2:
Input: candidates = [2,3,5], target = 8, A solution set is: [ [2,2,2,2], [2,3,3], [3,5] ]
一开始我是按下面的做法做的:
class Solution:
def combinationSum(self, candidates: 'List[int]', target: int) -> 'List[List[int]]':
ans = []
def recursive(i, sum_, seq):
if i >= len(candidates) or candidates[i] + sum_ >= target:
if sum_ + candidates[i] == target:
ans.append(seq + [candidates[i]])
return
recursive(i, sum_+candidates[i], seq+[candidates[i]])
if i < len(candidates)-1:
recursive(i + 1, sum_+candidates[i], seq+[candidates[i]])
recursive(i + 1, sum_, seq.copy())
recursive(0, 0, [])
return ans
我的思路是:在每一步,有三种选择:
- 将当前元素添加进序列中,然后依然停留在当前元素;
- 将当前元素添加进序列中,然后移动到下一个元素;
- 直接跳过当前元素,移动到下一个元素。
这么做,有一个bug,就是同一个序列可能会被添加进答案中多次。比如说,candidates = [2, 3], target = 5。有两种路径,会将[2, 3]添加进答案中:
- 添加第一个2,留在第一个元素上 -> 跳过第一个元素,移动到第二个元素 -> 添加第二个元素。
- 添加第一个2,移动到第二个元素上 -> 添加第二个元素。
因此,答案中可能会有重复的序列。为了消除这种重复,应该这样改写代码:
class Solution:
def combinationSum(self, candidates: 'List[int]', target: int) -> 'List[List[int]]':
ans = []
def recursive(i, sum_, seq):
if i >= len(candidates) or sum_ >= target:
if sum_ == target:
ans.append(seq)
return
for j in range(i, len(candidates)):
recursive(j, sum_+candidates[j], seq+[candidates[j]])
recursive(0, 0, [])
return ans
这个方法,可以这样理解:由candidates[0:n]组成的和为target的序列,可以分为n种,其中第i种为必包含candidates[i],且只包含来自candidates[i:n]的元素的序列。因此,要统计出所有第i种序列,只需要统计出所有由candidates[i:n]组成的和为target-candidates[i]的序列,为它们append一个candidates[i]即可。要统计后者可以使用递归。
48. Rotate Image
You are given an n x n 2D matrix representing an image.
Rotate the image by 90 degrees (clockwise).
Note:
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
Given input matrix = [ [1,2,3], [4,5,6], [7,8,9] ], rotate the input matrix in-place such that it becomes: [ [7,4,1], [8,5,2], [9,6,3] ]Example 2:
Given input matrix = [ [ 5, 1, 9,11], [ 2, 4, 8,10], [13, 3, 6, 7], [15,14,12,16] ], rotate the input matrix in-place such that it becomes: [ [15,13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7,10,11] ]
这道题更多的是需要多边界的掌控能力……可以看到,顺时钟旋转90度,其实就是对应位置的4个元素换了一下位置(比如,5 11 16 15,或者 1 10 2 14)。它们在位置上是有联系的。具体地说,matrix[i][j]会跟matrix[j][-i - 1], matrix[-i - 1][-j - 1], matrix[-j - 1][i]这三个元素换位。因此,只要访问左上角的i, j,再进行换位,就可以完成旋转。比较难的是确定边界。经过思考和debug,确定i的取值范围是[0, ceil(len(matrix)/2)],而j的取值范围是[0, len(matrix[0])//2]。
from math import ceil
class Solution:
def rotate(self, matrix: 'List[List[int]]') -> None:
if not matrix or not matrix[0]:
return
for i in range(ceil(len(matrix)/2)):
for j in range(len(matrix[0]) // 2):
matrix[i][j], matrix[j][-i - 1], matrix[-i - 1][-j - 1], matrix[-j - 1][i] = matrix[-j - 1][i], matrix[i][j], matrix[j][-i - 1], matrix[-i - 1][-j - 1]
这个人把下标简化了一下,用~i代替-i-1,也是可以的。这个答案提出了另外两种顺时钟旋转矩阵的方法。分别是:将矩阵的行上下翻转,再求其转置。
215. Kth Largest Element in an Array
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
Example 1:
Input: [3,2,1,5,6,4] and k = 2 Output: 5Example 2:
Input: [3,2,3,1,2,4,5,5,6] and k = 4 Output: 4
这道题的直觉做法是维护一个大小为k的最小堆,将每个元素push进堆中,然后pop出n-k个,保留k个。剩下的最小元素就是第k大的元素。这种做法固然好,但是有一个更加合适的算法,称为QuickSelect算法。它有点像快排。逆序快排的一种形式是,选择一个pivot,然后将所有大于pivot的元素移动到数组前面,后面的元素就是小于等于pivot的。设共有x个元素比pivot大,将pivot这个元素和arr[x]交换,这样arr[:x]是比pivot大的元素,arr[x+1:]的元素不大于pivot。对arr[:x]和arr[x+1:]继续用快排,直到完全排好为止。事实上,如果当前轮的pivot被放在arr[k-1]位置上,可以看出共有k-1个元素比pivot大,n-k+1个元素不大于pivot。那么pivot就是第k大的元素了。这样在快排的过程中,可以在完全排序好之前知道第k大的元素。
另外,快排会递归地排序arr[:x]和arr[x+1:]两部分。但是,我们的目的是为了找到第k大的元素。arr[:x]中的元素都比arr[x]大。如果x < k,显然第k大的元素不可能在arr[:x]中。所以不必去排序arr[:x]了,只用关注arr[x+1:]即可。如果x >= k,显然第k大的元素是在arr[:x]之中。所以也不必去排序arr[x+1:]。这个过程就像二分查找,每次平均能排除一半的候选项。
不过,即使QuickSelect这个方法在理论上很美妙,但提交给LeetCode,它的性能比堆排序差多了……不明白是为什么。
// heap
class Solution {
public:
int findKthLargest(vector<int> &nums, int k) {
std::priority_queue<int, std::vector<int>, std::greater<int>> pq;
for (int num : nums) {
pq.push(num);
if (pq.size() > k) pq.pop();
}
return pq.top();
}
};
// quick sort
class Solution {
int qsort(vector<int> &arr, int l, int r, int k) {
if (l >= r) return arr[l];
int pivot = arr[r], p = l, tmp;
for (int i = l; i <= r; ++i) {
if (arr[i] > pivot) tmp = arr[i], arr[i] = arr[p], arr[p] = tmp, ++p;
}
tmp = arr[p], arr[p] = arr[r], arr[r] = tmp;
// there is p elements greater than pivot
if (p == k - 1) {
return pivot;
} else if (p < k) {
// there are less than k elements greater than pivot
// the answer cannot be among these p elements
// so do not need to sort arr[:p]
return qsort(arr, p + 1, r, k);
} else {
return qsort(arr, l, p - 1, k);
}
}
public:
int findKthLargest(vector<int> &nums, int k) {
return qsort(nums, 0, nums.size()-1, k);
}
};
287. Find the Duplicate Number
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Example 1:
Input: [1,3,4,2,2]
Output: 2
Example 2:
Input: [3,1,3,4,2]
Output: 3
假设我们构造一个有n+1个节点的图,编号为0~n。对数组arr的每个元素arr[i] == x,我们在图中添加一条有向边,从节点i指向节点x。由于arr[1:n+1]共有n个元素,范围在1~n之间,所以这n个元素为节点1到n连接了共n条边。节点1到n之间必有环,否则边的数目不超过n-1。而节点0是无入度的,因为arr中没有值为0的元素。假设arr[0] == y。加上0->y这一条边,节点1到n中必有至少一个节点的入度大于1。假设这个节点的编号是d。由于有两条以上的有向边指向它,所以必有超过两个数组元素的值等于d,这意味着d就是我们要找的重复元素。也就是说,我们找重复元素的任务,等价于在图中找一个入度大于1的节点。
另一方面,从节点0出发,每次沿着一条边前进到下一个节点,肯定会走入一个环。这是因为每个节点都有出度(这条出边的目的节点号是节点对应的arr[i]的值)。环的入口在节点1到n之中,且它的入度大于1。这个节点的编号就是重复元素。至此,我们把寻找重复元素的任务,化成了在有环图中寻找环入口节点的任务。
要寻找环的入口,可以用Floyd’s Tortoise and Hare Algorithm。这个算法是比较常见的,我就不介绍了。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int slow = 0, fast = 0;
do {
slow = nums[slow]; // go to next node
fast = nums[nums[fast]]; // 2 steps
} while (slow != fast); // meet in circle
// suppose distance from start to entrance of circle is x
// distance from entrance to meet point is y
// distance from meet point to entrance is z
// then, slow goes (x + y) steps
// fast goes (x + y + z + y) steps (1 whole circle)
// then: 2 * (x + y) == (x + 2 * y + z) -> x == z
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
102. Binary Tree Level Order Traversal
Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
For example: Given binary tree
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7return its level order traversal as:
[ [3], [9,20], [15,7] ]
层次遍历是非常基本的知识。用一个队列来存储当前层的所有节点。设当前层有x个节点。在对该层遍历时,从队列中pop出x个节点,对它们访问后,将它们的非空孩子压入队列中。在遍历完最后一层后,队列会变空。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (!root) return {};
queue<TreeNode*> level;
vector<vector<int>> rtn;
level.push(root);
while (!level.empty()) {
rtn.push_back(vector<int>());
int level_num = level.size();
for (int i = 0; i < level_num; ++i) {
TreeNode *node = level.front(); level.pop();
rtn.back().push_back(node->val);
if (node->left) level.push(node->left);
if (node->right) level.push(node->right);
}
}
return rtn;
}
};
21. Merge Two Sorted Lists
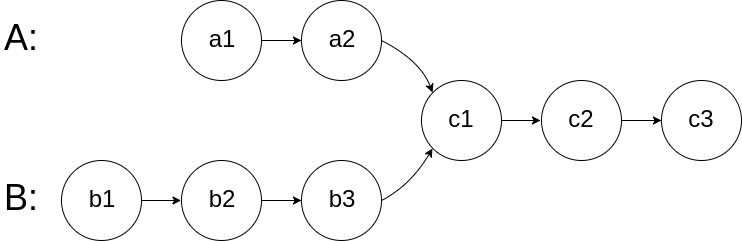
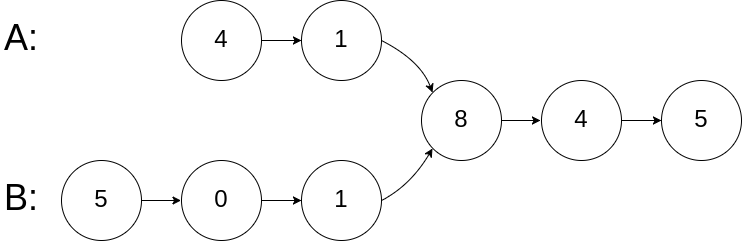
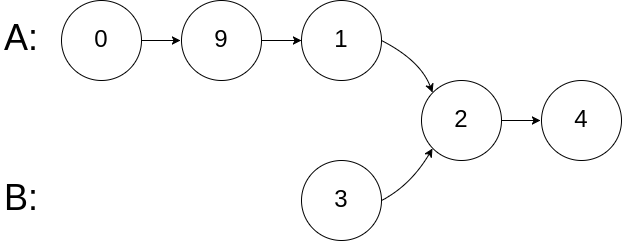
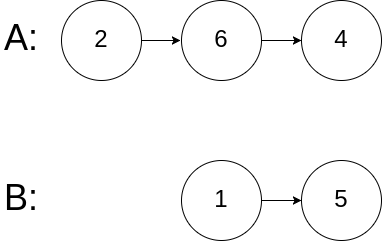
Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.
Example:
Input: 1->2->4, 1->3->4 Output: 1->1->2->3->4->4
为了方便,可以设置一个虚拟的头节点。同时遍历l1 l2链表,比较它们,将较小的节点接到虚拟头结点开始的链表中。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if (!l1) return l2;
if (!l2) return l1;
ListNode *head = new ListNode(0); // virtual head
ListNode *curr = head;
while (l1 && l2) {
if (l1->val < l2->val) curr->next = l1, l1 = l1->next;
else curr->next = l2, l2 = l2->next;
curr = curr->next;
}
if (l1) curr->next = l1;
if (l2) curr->next = l2;
curr = head->next;
delete head;
return curr;
}
};
62. Unique Paths
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
How many possible unique paths are there?
Above is a 7 x 3 grid. How many possible unique paths are there?
Example 1:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Right -> Down 2. Right -> Down -> Right 3. Down -> Right -> RightExample 2:
Input: m = 7, n = 3 Output: 28
非常基础的动态规划问题。用dp[i][j]表示到达grid[i][j]的路径数,那么
dp[i][j] = dp[i-1][j] + dp[i][j-1]
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0 for _ in range(n)] for _ in range(m)]
for i in range(m):
for j in range(n):
if i == 0 and j == 0:
dp[i][j] = 1
else:
if i > 0:
dp[i][j] += dp[i-1][j]
if j > 0:
dp[i][j] += dp[i][j-1]
return dp[-1][-1]
因为这个动态规划的累加是有序的,所以至多用一个一维数组就够了,用来记录dp[i-1][j]:
def uniquePaths(self, m: int, n: int) -> int:
dp = [0 for _ in range(n)]
for i in range(m):
for j in range(n):
if i == 0 and j == 0:
dp[j] = 1
else:
if i > 0:
# dp[i][j] += dp[i-1][j]. do nothing
pass
if j > 0:
dp[j] += dp[j-1]
return dp[-1]
时间复杂度为$O(mn)$。
64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example:
Input: [ [1,3,1], [1,5,1], [4,2,1] ] Output: 7 Explanation: Because the path 1→3→1→1→1 minimizes the sum.
这道题可以用动态规划解决。另dp[i][j]表示走到grid[i][j]的最小花费。显然有dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]。这里向62题一样,用一个一维的dp数组就可以了。
#define min(x, y) ( (x) < (y) ? (x) : (y) )
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if (!grid.size() || !grid[0].size()) return 0;
// dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
vector<int> dp(grid[0].size(), 0);
dp[0] = grid[0][0];
for (int j = 1; j < grid[0].size(); ++j) dp[j] = dp[j-1] + grid[0][j];
for (int i = 1; i < grid.size(); ++i) {
dp[0] += grid[i][0];
for (int j = 1; j < grid[0].size(); ++j)
dp[j] = min(dp[j-1], dp[j]) + grid[i][j];
}
return dp.back();
}
};
312. Burst Balloons
Given
nballoons, indexed from0ton-1. Each balloon is painted with a number on it represented by arraynums. You are asked to burst all the balloons. If the you burst ballooniyou will getnums[left] * nums[i] * nums[right]coins. Hereleftandrightare adjacent indices ofi. After the burst, theleftandrightthen becomes adjacent.Find the maximum coins you can collect by bursting the balloons wisely.
Note:
- You may imagine
nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.- 0 ≤
n≤ 500, 0 ≤nums[i]≤ 100Example:
Input: [3,1,5,8] Output: 167 Explanation: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
这是一个动态规划问题。为了方便,在数组的首尾各添加一个1,作为所谓的nums[-1] nums[n]。令dp[i][j]表示子数组nums[i:j+1]的气球全部爆炸以后能获得的最大金币数。在所有气球中,如果nums[p]是最后爆炸的,那么炸掉它获得的金币数是nums[p],炸掉它左边的所有气球获得的金币数是dp[0][p],炸掉右边的所有气球获得的金币数是dp[p+1][-1]。因此,就有dp[0][-1] == dp[0][p] + dp[p+1][-1] + nums[p]。尝试所有的p,可以求出一个最大的dp[0][-1],便是最终的答案。而求dp[0][p] dp[p+1][-1],可以用类似的思路递归求出。
class Solution {
vector<vector<int>> dp;
int recursive(vector<int> &nums, int i, int j) {
// calculate dp[i][j]
if (dp[i][j] != -1) return dp[i][j]; // already calculated
if (i + 1 == j) return 0; // no balloons left
// try p
int max_coin = -1, curr_coin;
for (int p = i + 1; p < j; ++p) {
curr_coin = recursive(nums, i, p) + recursive(nums, p, j) + nums[i] * nums[j] * nums[p];
if (curr_coin > max_coin) max_coin = curr_coin;
}
dp[i][j] = max_coin;
return max_coin;
}
public:
int maxCoins(vector<int>& nums) {
if (nums.empty()) return 0;
nums.push_back(1), nums.insert(nums.begin(), 1);
dp = vector<vector<int>>(nums.size(), vector<int>(nums.size(), -1));
return recursive(nums, 0, nums.size()-1);
}
};
96. Unique Binary Search Trees
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?
Example:
Input: 3 Output: 5 Explanation: Given n = 3, there are a total of 5 unique BST's: 1 3 3 2 1 \ / / / \ \ 3 2 1 1 3 2 / / \ \ 2 1 2 3
这是一道动态规划题。设dp[i]是节点数为i的二叉搜索树的数量。节点为i的二叉搜索树的根节点可以在1~i之间,设它的根节点为x,那么1~x-1这些节点必定在它的左子树中,x+1~i则在右子树上。所以它的左子树有x-1个节点,右子树有i-x个节点。左子树的形态共有dp[x-1]种,右子树的形态共有dp[i-x]种。因此,以x为根,节点数为n的二叉搜索树共有dp[x-1] * dp[i-x]种。
class Solution {
public:
int numTrees(int n) {
if (n <= 1) return n;
vector<int> dp(n+1, 0);
dp[0] = 1; // empty tree
for (int i = 1; i <= n; ++i) {
for (int x = 1; x <= i; ++x) {
dp[i] += dp[x-1] * dp[i-x];
}
}
return dp[n];
}
};
198. 213. 337. House Robber I & II & III
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.Example 2:
Input: [2,7,9,3,1] Output: 12 Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1). Total amount you can rob = 2 + 9 + 1 = 12.
第一道题可以用动态规划解决。设dp[i]是在nums[:i+1]之中抢劫,能抢到的最大金额。对于nums[i],有两种可能,要么抢劫它,那么dp[i] = dp[i-2] + nums[i];要么不抢劫它,那么dp[i] = dp[i-1]。这两种可能的最大值即是dp[i]的值。可以用两个变量来记录dp[i-2]和dp[i-1],那么就不用dp向量了。
#define max(x, y) ( (x) > (y) ? (x) : (y) )
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty()) return 0;
vector<int> dp(nums.size(), 0);
dp[0] = nums[0];
for (int i = 1; i < dp.size(); ++i) {
dp[i] = nums[i];
if (i > 1) dp[i] += dp[i-2];
dp[i] = max(dp[i], dp[i-1]);
}
return dp.back();
}
};
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: [2,3,2] Output: 3 Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.Example 2:
Input: [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.
和I几乎一样,只是nums[0]和nums[-1]挨在一起,不能同时被偷。那么,可以分别计算nums[0:-1]和nums[1:]被偷后的最大金额,再比较它们,取最大值为答案。
class Solution {
int _rob(vector<int>& nums, int l, int r) {
// max rob num of nums[l:r]
vector<int> dp(r - l, 0);
dp[0] = nums[l];
for (int i = 1; i < dp.size(); ++i) {
dp[i] = nums[i+l];
if (i > 1) dp[i] += dp[i-2];
dp[i] = max(dp[i], dp[i-1]);
}
return dp.back();
}
public:
int rob(vector<int>& nums) {
if (nums.empty()) return 0;
if (nums.size() == 1) return nums[0];
int rob1 = _rob(nums, 0, nums.size()-1), rob2= _rob(nums, 1, nums.size());
return max(rob1, rob2);
}
};
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Determine the maximum amount of money the thief can rob tonight without alerting the police.
Example 1:
Input: [3,2,3,null,3,null,1] 3 / \ 2 3 \ \ 3 1 Output: 7 Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.Example 2:
Input: [3,4,5,1,3,null,1] 3 / \ 4 5 / \ \ 1 3 1 Output: 9 Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
这次房子不是线性排列的,而是呈二叉树形状排列的。不能同时偷相邻的两个房子,即是不能同时偷一个父节点和它的孩子。思路和前面两个基本一样。令dp[node]为以节点node为根的子树所能抢到的最大金额。对于一个节点node,要么抢它,获得最多node->val + dp[node->left->left] + dp[node->left->right] + dp[node->right->left] + dp[node->right->right]这么多钱(node的两个孩子不能抢,只能跨代抢);要么不抢,获得最多dp[node->left] + dp[node->right]这么多钱。这两个数值相比较,取较大的作为dp[node]。
class Solution {
std::map<TreeNode*, int> dp;
int get_dp(TreeNode *node) {
if (dp.find(node) != dp.end()) return dp[node];
int not_rob = 0;
if (node->left) not_rob += get_dp(node->left);
if (node->right) not_rob += get_dp(node->right);
int rob = node->val;
if (node->left) {
if (node->left->left) rob += get_dp(node->left->left);
if (node->left->right) rob += get_dp(node->left->right);
}
if (node->right) {
if (node->right->left) rob += get_dp(node->right->left);
if (node->right->right) rob += get_dp(node->right->right);
}
dp[node] = max(not_rob, rob);
return dp[node];
}
public:
int rob(TreeNode* root) {
if (!root) return 0;
return get_dp(root);
}
};
121.122.123.188.309.714 Best Time to Buy and Sell Stock I & II & III & IV & Cooldown & Transaction Fee
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example 1:
Input: [7,1,5,3,6,4] Output: 5 Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Not 7-1 = 6, as selling price needs to be larger than buying price.Example 2:
Input: [7,6,4,3,1] Output: 0 Explanation: In this case, no transaction is done, i.e. max profit = 0.
遍历每一天的股票价格,在当天能够获得的最大收益,是当天价格减去过去最低的价格。所以用一个变量来记住过去最低的价格,比较今天是否可以卖出比以往更高的收益即可。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int min_price = 0x7fffffff, max_profit = 0;
for (int price: prices) {
if (price - min_price > max_profit) max_profit = price - min_price;
if (price < min_price) min_price = price;
}
return max_profit;
}
};
You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).
Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [7,1,5,3,6,4] Output: 7 Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4. Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.Example 2:
Input: [1,2,3,4,5] Output: 4 Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4. Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.Example 3:
Input: [7,6,4,3,1] Output: 0 Explanation: In this case, no transaction is done, i.e. max profit = 0.
如果第i+1天的股价比第i天高,且手中有股票,那么肯定不会在第i天卖,而是等到第i+1天卖。同样的,如果第i+1天股价比第i天低,那肯定不会留到第i+1天才卖。可以给股价变化画一个曲线图。在股价上升时我们持有股票;在股价下降时空仓,这样每次股价的上升我们都能赚到,每次股价下跌我们都能避免损失。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
int profit = 0;
for (int i = 1; i < prices.size(); ++i) {
if (prices[i] > prices[i-1])
profit += prices[i] - prices[i-1];
}
return profit;
}
};
You may complete at most two (k) transactions.
Example 1:
Input: [3,3,5,0,0,3,1,4] Output: 6 Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3. Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.Example 2:
Input: [1,2,3,4,5] Output: 4 Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4. Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.Example 3:
Input: [7,6,4,3,1] Output: 0 Explanation: In this case, no transaction is done, i.e. max profit = 0.
III和IV是类似的。III规定最多可以买卖2次,IV规定最多可以买卖k次。可以用动态规划来解决这个问题。令dp[k][i]为在第1~i天中,进行至多k次交易能获得的最大收益。易知dp的转移公式是dp[k][i] = max(dp[k][i-1], prices[i-1]-prices[j-1]+dp[k-1][j-1])。第一项,dp[k][i-1],表示第i天不交易,所以能获得的最大收益和前一天的一样;prices[i-1]-prices[j-1]+dp[k-1][j-1]表示今天卖出第j天买入的股票。由于对每个i,需要对1~i-1之间的所有j求prices[i-1]-prices[j-1]+dp[k-1][j-1],然后计算最大值,会导致时间复杂度高达O(kn^2),提交超时。通过观察,可以发现,求prices[i-1]-prices[j-1]+dp[k-1][j-1]大部分是冗余的。可以在i的迭代中记录max_j(prices[i-1]-prices[j-1]+dp[k-1][j-1]),以省去内层循环。
// 为了方便,从1开始算天数,而非通常的从0开始算天数
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
// dp[k][i] = max(dp[k][i-1], prices[i]-prices[j]+dp[k-1][j-1])
vector<vector<int>> dp(3, vector<int>(prices.size()+1, 0));
for (int k = 1; k <= 2; ++k) {
for (int i = 2; i <= prices.size(); ++i) {
int max_profit = dp[k][i-1], curr_profit;
for (int j = 1; j < i; ++j) {
curr_profit = prices[i-1] - prices[j-1] + dp[k-1][j-1];
if (curr_profit > max_profit) max_profit = curr_profit;
}
dp[k][i] = max_profit;
}
}
return dp[2][prices.size()];
}
};
// 上面的答案时间复杂度为O(kn^2),超时了。按照原文的建议,删改了最内层循环
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
// dp[k][i] = max(dp[k][i-1], prices[i]-prices[j]+dp[k-1][j-1])
vector<vector<int>> dp(3, vector<int>(prices.size()+1, 0));
for (int k = 1; k <= 2; ++k) {
// -prices[j-1]+dp[k-1][j-1]
int max_profit = -prices[0], curr_profit;
for (int i = 2; i <= prices.size(); ++i) {
curr_profit = -prices[i-2] + dp[k-1][i-2];
if (curr_profit > max_profit) max_profit = curr_profit;
// prices[i-1]-prices[j-1]+dp[k-1][j-1]
curr_profit = prices[i-1] + max_profit;
dp[k][i] = curr_profit > dp[k][i-1] ? curr_profit : dp[k][i-1];
}
}
return dp[2][prices.size()];
}
};
IV规定最多可以买卖k次。简单地将III的答案改造了一下,会发现在k较大时,生成dp数组(k*n维)可能不够内存,而且循环轮数也过多。因此在III的基础上,还需要对k进行优化。显然,dp被顺序遍历,是可以优化成一个一维数组的。其次,在k >= n/2时,问题就退化到了II,可以在线性时间内解决。
class Solution {
int maxProfit_II(vector<int>& prices) {
if (prices.size() <= 1) return 0;
int profit = 0;
for (int i = 1; i < prices.size(); ++i) {
if (prices[i] > prices[i-1])
profit += prices[i] - prices[i-1];
}
return profit;
}
public:
int maxProfit(int K, vector<int> &prices) {
if (prices.size() <= 1) return 0;
if (K >= prices.size()/2) return maxProfit_II(prices);
// dp[k][i] = max(dp[k][i-1], prices[i]-prices[j]+dp[k-1][j-1])
vector<int> dp_k(vector<int>(prices.size()+1, 0));
vector<int> dp_k_1(vector<int>(prices.size()+1, 0)); // dp[k-1]
for (int k = 1; k <= K; ++k) {
// -prices[j-1]+dp[k-1][j-1]
int max_profit = -prices[0], curr_profit;
for (int i = 2; i <= prices.size(); ++i) {
curr_profit = -prices[i-2] + dp_k_1[i-2];
if (curr_profit > max_profit) max_profit = curr_profit;
// prices[i-1]-prices[j-1]+dp[k-1][j-1]
curr_profit = prices[i-1] + max_profit;
dp_k[i] = curr_profit > dp_k[i-1] ? curr_profit : dp_k[i-1];
}
dp_k_1 = dp_k;
}
return dp_k[prices.size()];
}
};
You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
- After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2] Output: 3 Explanation: transactions = [buy, sell, cooldown, buy, sell]
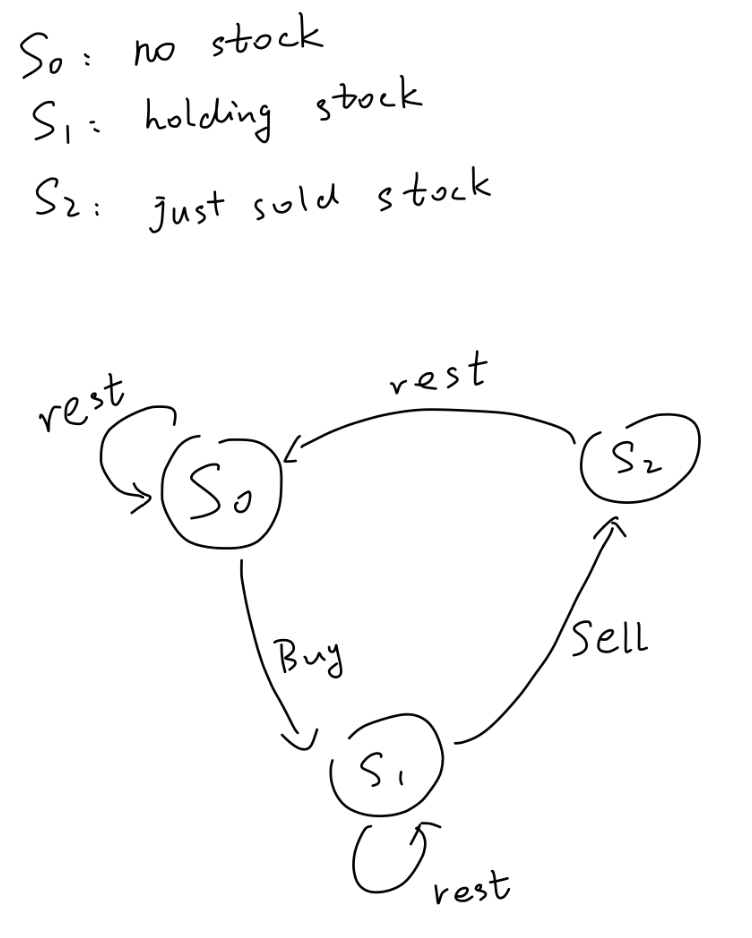
这题刷新了我的知识范围,这篇回答使用了状态机来构造动态规划转移公式,非常有启发性。如下图,在某一时刻,我们处于三个状态中的某一个中:
S0:没有持有股票;S1:持有股票,等待抛售;S2:刚刚卖完股票,正在冷却。
我们用三个数组,分别记录在第i天时处于这三个状态的最大获利金额。这三个dp数组的转移公式显而易见:
S0[i] = max(S0[i-1], S2[i-1])S1[i] = max(S0[i-1] - prices[i], S1[i-1]),从S0买入prices[i]S2[i] = S1[i-1] + prices[i],从S1卖出prices[i]
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
vector<int> S0(prices.size()), S1(prices.size()), S2(prices.size());
S0[0] = 0, S1[0] = -prices[0], S2[0] = -0x7fffffff; // cannot be at S2
for (int i = 1; i < prices.size(); ++i) {
S0[i] = std::max(S0[i-1], S2[i-1]);
S1[i] = std::max(S0[i-1] - prices[i], S1[i-1]);
S2[i] = S1[i-1] + prices[i];
}
return std::max(S0.back(), S2.back());
}
};
You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction.
Example 1:
Input: prices = [1, 3, 2, 8, 4, 9], fee = 2 Output: 8 Explanation: The maximum profit can be achieved by: Buying at prices[0] = 1Selling at prices[3] = 8Buying at prices[4] = 4Selling at prices[5] = 9The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
有了上面cooldown状态机的启发,做这一题就非常简单了^_^这次只需要S0和S1两个状态,在S1(持有股票)转移到S0(没有持有股票)状态时,要额外扣除手续费。状态机图比cooldown简单很多。
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
if (prices.size() <= 1) return 0;
vector<int> S0(prices.size()), S1(prices.size());
S0[0] = 0, S1[0] = -prices[0];
for (int i = 1; i < prices.size(); ++i) {
S0[i] = std::max(S0[i-1], S1[i-1] + prices[i] - fee);
S1[i] = std::max(S0[i-1] - prices[i], S1[i-1]);
}
return S0.back();
}
};
// 对内存进行优化,只需要两个变量来记录状态数据
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
if (prices.size() <= 1) return 0;
int S0 = 0, S1 = -prices[0], tmp;
for (int i = 1; i < prices.size(); ++i) {
tmp = S0;
S0 = std::max(S0, S1 + prices[i] - fee);
S1 = std::max(tmp - prices[i], S1);
}
return S0;
}
};
11. Container With Most Water
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7] Output: 49
选择两块挡板,水的体积由挡板组成的容器的高度(较矮的挡板的高度)和宽度(挡板的距离)相乘得到。首先我们考虑由最左和最右两块挡板组成的容器。如果最左的挡板a比最右的挡板b矮,那么容器a b的高度即是a的高度。假设存在一个容器体积比a b组成的容器体积大,它可不可能由a组成?不可能,因为这个容器的宽度肯定比a b小,而且它的高度也不大于a,所以它的体积肯定比a b小。所以,我们在继续寻找更大容器的过程中,就不必再考虑挡板a了。接下来考虑的是宽度仅次于a b的容器c b(c为a右边的挡板)。根据同样的思路,不断缩小搜索空间。
class Solution {
public:
int maxArea(vector<int>& height) {
int low = 0, high = height.size()-1, max_area = 0;
while (low < high) {
max_area = max(max_area, (high - low) * min(height[low], height[high]));
if (height[low] < height[high]) low++;
else high--;
}
return max_area;
}
};
394. Decode String
Given an encoded string, return its decoded string.
The encoding rule is:
k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.
Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there won’t be input like
3aor2[4].Examples:
s = "3[a]2[bc]", return "aaabcbc". s = "3[a2[c]]", return "accaccacc". s = "2[abc]3[cd]ef", return "abcabccdcdcdef".
这道题可以用递归来做,也可以用栈来做。用栈更加复杂,需要先分析什么东西要被LIFO地保存,什么时候被取出。考虑下面这种情况:3[ab4[bc]d]。在进入最里层的括号(4[bc])后,我们需要一个变量cur来存储最里层包含的字符串,在收集完成后将它复制4次,和它外层的字符串(ab)相连接。外层不完整的字符串适合放在栈中,在它下一层的字符串成功获取并复制后,将它们拼接,然后继续完善这层的字符串。这层的字符串完成后,从栈中取出它上一层的不完整字符串,将它们拼接,然后继续完成上一层的字符串……可以看出,将某一层未完成的字符串放入栈中是LIFO的。
class Solution {
public:
string decodeString(string s) {
stack<int> repeat_num;
stack<string> incomplete;
string cur, last;
int repeat;
for (int i = 0, len = s.length(); i < len; ++i) {
if (isdigit(s[i])) {
int val = 0;
while (isdigit(s[i]))
val = val * 10 + (s[i] - '0'), ++i;
--i;
repeat_num.push(val);
} else if (s[i] == '[') {
incomplete.push(cur);
cur = "";
} else if (s[i] == ']') {
repeat = repeat_num.top();
last = incomplete.top();
repeat_num.pop(), incomplete.pop();
while (repeat--) last += cur;
cur = last;
} else cur += s[i];
}
return cur;
}
};
543. Diameter of Binary Tree
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
Example: Given a binary tree
1 / \ 2 3 / \ 4 5Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
Note: The length of path between two nodes is represented by the number of edges between them.
这题可以用类似动态规划的思路做。假设有一条路径通过节点node,并且node是这条路径上最高的节点,那么要让这条路径最长,它肯定通达了node左右子树的最深处。令叶子节点的高度为1,那么这条路径的最长长度,其实就是左右子树的高度和。从叶子结点向上,逐层地求出以某个节点为最高节点的路径的最长长度。这个过程可以整合在为树求高度的过程之中。
class Solution {
int ans;
int getHeight(TreeNode *node) {
if (!node) return 0;
int left_h = getHeight(node->left), right_h = getHeight(node->right);
if (left_h + right_h > ans) ans = left_h + right_h;
return std::max(left_h, right_h) + 1;
}
public:
int diameterOfBinaryTree(TreeNode* root) {
ans = 0;
getHeight(root);
return ans;
}
};
621. Task Scheduler
Given a char array representing tasks CPU need to do. It contains capital letters A to Z where different letters represent different tasks. Tasks could be done without original order. Each task could be done in one interval. For each interval, CPU could finish one task or just be idle.
However, there is a non-negative cooling interval n that means between two same tasks, there must be at least n intervals that CPU are doing different tasks or just be idle.
You need to return the least number of intervals the CPU will take to finish all the given tasks.
Example:
Input: tasks = ["A","A","A","B","B","B"], n = 2 Output: 8 Explanation: A -> B -> idle -> A -> B -> idle -> A -> B.
显然,时钟周期数和最频繁的任务的任务数是有关的。假设最频繁的任务A有x个,那么需要的时钟周期起码是(x - 1) * (n + 1) + 1个。在这段时间的间隙里,可以插入其它任务。思路类似于贪心算法,先做任务数最大的任务,然后做数量次之的任务。
class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
unordered_map<char,int> mp;
int count = 0;
for(auto e : tasks) {
mp[e]++;
count = max(count, mp[e]);
}
int ans = (count-1) * (n+1);
for(auto e : mp) if (e.second == count) ans++;
// counterexample: AAABBBCCDDEF, n = 2
return max((int)tasks.size(), ans);
}
};
42. Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6
凭直觉就能感受到,第i个槽可以存的水的水位是它左边的槽最高高度和右边的槽的最高高度的较小值。减去这个水槽的高度,就是能存的水的体积。
class Solution {
public:
int trap(vector<int>& height) {
if (height.empty()) return 0;
vector<int> max_left(height.size()), max_right(height.size());
int cur_max = 0;
for (int i = 0; i < height.size(); ++i) {
max_left[i] = cur_max;
if (height[i] > cur_max) cur_max = height[i];
}
cur_max = 0;
for (int i = height.size()-1; i >= 0; --i) {
max_right[i] = cur_max;
if (height[i] > cur_max) cur_max = height[i];
}
int rtn = 0;
for (int i = 0; i < height.size(); ++i) {
cur_max = std::min(max_left[i], max_right[i]);
if (cur_max > height[i]) rtn += cur_max - height[i];
}
return rtn;
}
};
下面是空间复杂度为O(1)的做法。不需要来回两趟遍历,而是从左右同时访问height。利用两个指针left right来指示左右当前位置。利用两个变量max_left max_right来存储height[:left]中元素的最大值和height[right+1:]中元素的最大值。如果max_left < max_right,显然,left所在位置的最高水位是受限于max_left的(它左边最高就是max_left了,右边有比max_left更高的高度)。right所在位置不一定会受限于max_left,因为在height[left+1:right]之中可能会有一个比max_left更高的高度,为right提高水位。因此,在max_left < max_right时,我们就考虑left;如果height[left] > max_left,则更新max_left = height[left]。此时在left处无法接雨水。如果height[left] < max_left,那么left处可以接雨水,体积为max_left - height[left]。在max_left > max_right时分析类似。
class Solution {
public:
int trap(vector<int>& height) {
if (height.empty()) return 0;
int max_left = 0, max_right = 0, left = 0, right = height.size() - 1;
int rtn = 0;
while (left <= right) {
if (max_left < max_right) {
if (height[left] > max_left) max_left = height[left];
else rtn += max_left - height[left];
++left;
} else {
if (height[right] > max_right) max_right = height[right];
else rtn += max_right - height[right];
--right;
}
}
return rtn;
}
};
114. Flatten Binary Tree to Linked List
Given a binary tree, flatten it to a linked list in-place.
For example, given the following tree:
1 / \ 2 5 / \ \ 3 4 6The flattened tree should look like:
1 \ 2 \ 3 \ 4 \ 5 \ 6
先把左子树和右子树变成链表,然后将它们和根节点连接起来,整棵树就变成了一个链表。因此,可以递归地将左右子树先变成链表,再将根节点和它们连接起来。
class Solution {
public:
void flatten(TreeNode* node) {
if (!node) return;
flatten(node->left), flatten(node->right);
TreeNode *curr = node->left;
if (!curr) return;
while (curr->right) curr = curr->right;
curr->right = node->right;
node->right = node->left, node->left = nullptr;
}
};
附另一种写法,非常地简洁巧妙。
class Solution {
TreeNode *prev = NULL;
public:
void flatten(TreeNode* root) {
if (root == NULL) return;
flatten(root->right), flatten(root->left);
root->left = NULL, root->right = prev;
prev = root;
}
};
494. Target Sum
You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols
+and-. For each integer, you should choose one from+and-as its new symbol.Find out how many ways to assign symbols to make sum of integers equal to target S.
Example 1:
Input: nums is [1, 1, 1, 1, 1], S is 3. Output: 5 Explanation: -1+1+1+1+1 = 3 +1-1+1+1+1 = 3 +1+1-1+1+1 = 3 +1+1+1-1+1 = 3 +1+1+1+1-1 = 3 There are 5 ways to assign symbols to make the sum of nums be target 3.
这道题用DFS来做,可以AC,但是效率不高。这位兄弟提出了一个更好的办法,他将数组分成了P和N两个部分,其中P的符号将是正的,N的符号将是负的。这道题要求sum(P) - sum(N) = target,两边同时加上sum(nums),可以得到2 * sum(P) = target + sum(nums)。因此,问题就归化成了一个等价问题:在nums中找出若干数,使其和为(target + sum(nums)) / 2。这就变成了一个01背包问题:在nums的物品中找出若干物品,使其填满大小为(target + sum(nums)) / 2。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum_ = accumulate(nums.begin(), nums.end(), 0);
if (sum_ < S || -sum_ > S) return 0;
sum_ += S;
if (sum_ % 2 == 1) return 0; // should be even
sum_ /= 2;
vector<int> dp(sum_+1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); ++i) {
for (int j = sum_; j >= nums[i]; --j)
dp[j] = dp[j] + dp[j-nums[i]];
}
return dp[sum_];
}
};
105. Construct Binary Tree from Preorder and Inorder Traversal
Given preorder and inorder traversal of a tree, construct the binary tree.
Note: You may assume that duplicates do not exist in the tree.
For example, given
preorder = [3,9,20,15,7] inorder = [9,3,15,20,7]Return the following binary tree:
3 / \ 9 20 / \ 15 7
一棵树的前序遍历序列,按照[根节点 [左子树遍历序列] [右子树遍历序列]]这样排列。一棵树的中序遍历序列,按照[[左子树遍历序列] 根节点 [右子树遍历序列]]这样排列。我们可以从前序遍历序列的第一个元素发现根节点的值。在中序遍历序列中定位根节点,其左边序列的元素个数就是左子树的节点个数。在前序遍历序列中顺序截取这个长度的序列,就是左子树前序遍历的序列。从左子树前序遍历序列和左子树中序遍历序列,又可以递归地构造左子树。同理,右子树也能从其前序遍历序列和中序遍历序列递归地构造。
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder,
int pl = -1, int pr = -1, int il = -1, int ir = -1) {
if (preorder.empty() || inorder.empty()) return nullptr;
// construct with preorder[pl:pr], inorder[il:ir]
if (pl == -1) pl = 0, il = 0, pr = preorder.size(), ir = inorder.size();
if (pl == pr || il == ir) return nullptr;
TreeNode *root = new TreeNode(preorder[pl]);
int root_pos = std::find(inorder.begin()+il, inorder.end()+ir, preorder[pl]) - inorder.begin();
int left_len = root_pos - il;
root->left = buildTree(preorder, inorder, pl+1, pl+1+left_len, il, il+left_len);
root->right = buildTree(preorder, inorder, pl+1+left_len, pr, root_pos+1, ir);
return root;
}
};
70. Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 stepsExample 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
这是典型的动态规划问题。令dp[i]等于爬i阶的方法数。显然,dp[i] = dp[i-1] + dp[i-2]。可以用两个变量来代替dp[i-1]和dp[i-2]进行优化。
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
// dp[1], dp[2]
int dp_1 = 1, dp_2 = 2, dp;
for (int i = 3; i <= n; ++i) {
dp = dp_1 + dp_2;
dp_1 = dp_2, dp_2 = dp;
}
return dp_2;
}
};
53. Maximum Subarray
Given an integer array
nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.Example:
Input: [-2,1,-3,4,-1,2,1,-5,4], Output: 6 Explanation: [4,-1,2,1] has the largest sum = 6.
假设nums[i:j]是和最大的序列。那么,它的前缀nums[i:k], k < j,和肯定不会小于0。因为如果有前缀和小于0,那么去掉它得到的序列,和会更大。因此,可以线性地遍历nums,同时累加元素,如果当前累加值小于0,则舍弃截止到当前的元素之前的序列,因为往后的序列不可能带上之前的序列作为前缀。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int cur = 0, max_ = -0x7fffffff;
for (int n: nums) {
cur += n;
if (cur > max_) max_ = cur;
if (cur < 0) cur = 0;
}
return max_;
}
};
101. Symmetric Tree
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree
[1,2,2,3,4,4,3]is symmetric:1 / \ 2 2 / \ / \ 3 4 4 3But the following
[1,2,2,null,3,null,3]is not:1 / \ 2 2 \ \ 3 3
代码胜过千言万语……
class Solution {
bool recursive(TreeNode *A, TreeNode *B) {
if (A == NULL && B == NULL) return true;
// not symmetric
if (A == NULL || B == NULL) return false;
if (A->val != B->val) return false;
return recursive(A->left, B->right) && recursive(A->right, B->left);
}
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return recursive(root->left, root->right);
}
};
297. Serialize and Deserialize Binary Tree
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Example:
You may serialize the following tree: 1 / \ 2 3 / \ 4 5 as "[1,2,3,null,null,4,5]"Clarification: The above format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
Note: Do not use class member/global/static variables to store states. Your serialize and deserialize algorithms should be stateless.
对树进行前序遍历,每访问一个节点,就向序列加入该节点的值。如果是空节点,就向序列加入一个表示空节点的符号。这样得到的前序遍历序列可以唯一地表示一棵树。在反序列化时,依然是前序遍历,每碰到一个数值则创建一个节点,碰到空节点符号则跳过当前分支。为了效率,我偷偷改了原题的接口,把返回值从string类型改成了char*类型。我把int数组指针显式转换成了char*指针,在反序列化时将其变回int*即可。不过这种做法存在内存泄漏的隐患,代码风格并不好。要认真做题的话还是看这个。
class Codec {
vector<int> sequence;
int* arr;
void preorder(TreeNode* node) {
if (!node) {
sequence.push_back(0x7fffffff);
return;
}
sequence.push_back(node->val);
preorder(node->left);
preorder(node->right);
}
TreeNode* de_preorder() {
int val = *arr++;
if (val == 0x7fffffff) return nullptr;
TreeNode* root = new TreeNode(val);
root->left = de_preorder(), root->right = de_preorder();
return root;
}
public:
// Encodes a tree to a single string.
char* serialize(TreeNode* root) {
sequence.clear();
preorder(root);
int *arr = new int[sequence.size() + 1];
std::copy(sequence.begin(), sequence.end(), arr);
return (char*) arr;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(char *data) {
arr = (int*)data;
TreeNode* node = de_preorder();
delete[] data;
return node;
}
};
17. Letter Combinations of a Phone Number
Given a string containing digits from
2-9inclusive, return all possible letter combinations that the number could represent.A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example:
Input: "23" Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
没啥好说的,非常简单的一个回溯问题。
class Solution {
static vector<string> map;
vector<string> rtn;
void dfs(string &digits, string &prefix, int i) {
if (i >= digits.length()) {
rtn.push_back(prefix);
return;
}
for (char c : map[digits[i]-'2']) {
prefix += c;
dfs(digits, prefix, i + 1);
prefix.pop_back();
}
}
public:
vector<string> letterCombinations(string digits) {
if (!digits.length()) return {};
rtn.clear();
string prefix = "";
dfs(digits, prefix, 0);
return rtn;
}
};
vector<string> Solution::map = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
200. Number of Islands
Given a 2d grid map of
'1's (land) and'0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.Example 1:
Input: 11110 11010 11000 00000 Output: 1Example 2:
Input: 11000 11000 00100 00011 Output: 3
每发现一个格子是陆地,就把它置为0,然后DFS它的上下左右相邻格子。这样在完整访问完一块陆地后,它所有的格子都变成0,在后续的搜索中就不会再被找到。
class Solution {
void explore_island(vector<vector<char>> &grid, int i, int j) {
// set the area of the island to '0'
grid[i][j] = '0';
if (i < grid.size() - 1 && grid[i+1][j] == '1') explore_island(grid, i + 1, j);
if (i > 0 && grid[i-1][j] == '1') explore_island(grid, i - 1, j);
if (j < grid[0].size() - 1 && grid[i][j+1] == '1') explore_island(grid, i, j + 1);
if (j > 0 && grid[i][j-1] == '1') explore_island(grid, i, j - 1);
}
public:
int numIslands(vector<vector<char>>& grid) {
if (!grid.size() || !grid[0].size()) return 0;
int count = 0;
for (int i = 0, ie = grid.size(); i < ie; ++i) {
for (int j = 0, je = grid[0].size(); j < je; ++j) {
if (grid[i][j] == '1') {
explore_island(grid, i, j);
++count;
}
}
}
return count;
}
};
1.15. Two Sum & Three Sum
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly* one solution, and you may not use the *same element twice.
Example:
Given nums = [2, 7, 11, 15], target = 9, Because nums[0] + nums[1] = 2 + 7 = 9, return [0, 1].
用一个哈希表保存遍历过的数和它的下标。在访问一个元素nums[i]时,先看看哈希表里是否储存了target-nums[i],如果有,就返回它们的下标。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> my_map;
for (int i = 0; i < nums.size(); ++i) {
if (my_map.find(target-nums[i]) != my_map.end())
return {my_map[target-nums[i]], i};
my_map[nums[i]] = i;
}
return {};
}
};
Given an array
numsof n integers, are there elements a, b, c innumssuch that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.Note:
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4], A solution set is: [ [-1, 0, 1], [-1, -1, 2] ]
这道题只能在O(n^2)时间复杂度下解决,所以我先将数组排序,遍历数组。对于数组元素nums[i],按low high指针的方法在nums[i+1:]中找出两个和等于-nums[i]的数,这三个数的和即为0。注意题目要求返回答案中不能有重复项。所以在当前访问元素等于它上个元素时,必须跳过这个元素,否则结果就会出现重复。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> rtn;
sort(nums.begin(), nums.end());
int low, high, sum, target;
for (int i = 0; i < nums.size(); ++i) {
if (i > 0 && nums[i] == nums[i-1]) continue;
low = i + 1, high = nums.size() - 1, target = -nums[i];
while (low < high) {
sum = nums[low] + nums[high];
if (sum == target) {
rtn.push_back({nums[i], nums[low], nums[high]});
do { ++low; } while (low < high && nums[low] == nums[low-1]);
// do { --high; } while (low < high && nums[high] == nums[high+1]);
}
else if (sum < target) ++low;
else --high;
}
}
return rtn;
}
};
252.253. Meeting Room & II
给定一个会议时间安排的数组,每个会议时间都会包括开始和结束的时间 [[s1,e1],[s2,e2],…] (si < ei),请你判断一个人是否能够参加这里面的全部会议。
示例 1:
输入: [[0,30],[5,10],[15,20]] 输出: false
示例 2:
输入: [[7,10],[2,4]] 输出: true
将会议按开始时间排序,如果前一个会议的结束时间晚于下一个会议的开始时间,那么无法参加。
class Solution {
public:
bool canAttendMeetings(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end(), [](vector<int> &i1, vector<int> &i2) { return i1[0] < i2[0];} );
for (int i = 1; i < intervals.size(); ++i) {
if (intervals[i][0] < intervals[i-1][1]) return false;
}
return true;
}
};
给定一个会议时间安排的数组,每个会议时间都会包括开始和结束的时间 [[s1,e1],[s2,e2],…] (si < ei),为避免会议冲突,同时要考虑充分利用会议室资源,请你计算至少需要多少间会议室,才能满足这些会议安排。
示例 1:
输入: [[0, 30],[5, 10],[15, 20]] 输出: 2 示例 2:
输入: [[7,10],[2,4]] 输出: 1
这道题我一开始的想法是,将会议按开始时间从小到大排序,然后遍历会议。使用一个优先队列(最小堆)来存储之前的尚未结束的会议的结束时间。如果当前会议的开始时间不小于队列中最小的结束时间,那么将该最小时间移除。重复这个操作直到无法移除为止。然后将当前会议的结束时间放入队列中。队列的大小就代表当前正在进行中的会议。全局中队列的最大大小显然就是会议室的必须数量。
在题解区的一篇回答更加优雅地解决了这个问题。将所有会议的开始时间和结束时间放在同个数组中,排序,然后遍历这个数组。每遇到一个开始的时间,当前会议数量就加一。每遇到一个结束的时间,当前会议数量就减一。我们无需管某个结束时间属于哪个正在进行中的会议,我们只需要知道有一个会议刚刚结束,同时进行中的会议数量减少了一就可以。
class Solution {
public:
int minMeetingRooms(vector<vector<int>>& intervals) {
vector<int> start(intervals.size()), end(intervals.size());
for (int i = 0; i < intervals.size(); ++i) start[i] = intervals[i][0], end[i] = intervals[i][1];
sort(start.begin(), start.end());
sort(end.begin(), end.end());
int start_idx = 0, end_idx = 0, curr = 0, max_num = 0;
while (start_idx < start.size()) {
while (start[start_idx] >= end[end_idx]) ++end_idx, --curr;
++curr, ++start_idx;
if (max_num < curr) max_num = curr;
}
return max_num;
}
};
437. Path Sum III
You are given a binary tree in which each node contains an integer value.
Find the number of paths that sum to a given value.
The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).
The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.
Example:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8 10 / \ 5 -3 / \ \ 3 2 11 / \ \ 3 -2 1 Return 3. The paths that sum to 8 are: 1. 5 -> 3 2. 5 -> 2 -> 1 3. -3 -> 11
这题我做的方法比较笨,我在访问一个节点时,求出了通往它所有子嗣的路径的路径和,然后判断这里面是否有和等于sum的路径。非常低效,不值一提。
这个答案是我见过的最好的。在访问一个节点node时,将它的节点值修改为从根节点到这个节点的路径的路径和。如果它的祖先之中,有一个节点到根节点的路径和等于node->val - sum,则它们之间的路径和为node->val - (node->val - sum) = sum。所以,在访问node时,如果能事先知道它的祖先之中有多少个节点的节点值为node->val - sum,就可以马上知道以node为路径终点的路径中有多少条的路径和是sum。这里用了一个哈希表来保存祖先的路径和。代码结构非常巧妙,艺高人胆大。
class Solution {
public:
int help(TreeNode* root, int sum, unordered_map<int, int>& store, int pre) {
if (!root) return 0;
root->val += pre;
int res = (root->val == sum) + (store.count(root->val - sum) ? store[root->val - sum] : 0);
store[root->val]++;
res += help(root->left, sum, store, root->val) + help(root->right, sum, store, root->val);
store[root->val]--;
return res;
}
int pathSum(TreeNode* root, int sum) {
unordered_map<int, int> store;
return help(root, sum, store, 0);
}
};
75. Sort Colors
Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.
Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.
Note: You are not suppose to use the library’s sort function for this problem.
Example:
Input: [2,0,2,1,1,0] Output: [0,0,1,1,2,2]
维护两个指针low和high。规定nums[:low]应该全是0,nums[high+1:]应该全是2。每访问到一个0,就将它和nums[low]互换,并让low加一。每访问到一个2,就将它和nums[high]互换,并让high减一。在访问到high后,就没有未访问的元素了。low到high之间的元素应该全是1。这里要注意的是当前访问元素mid的位置。mid应该始终不小于low。当和nums[high]互换以后,mid不应该加一,因为换来的这个数(新的nums[mid])还没有被访问过。
class Solution {
public:
void sortColors(vector<int>& nums) {
if (nums.size() == 0) return;
int low = 0, high = nums.size() - 1, mid = 0;
while (mid <= high) {
if (nums[mid] == 0) {
swap(nums[mid], nums[low++]);
mid = low;
}
else if (nums[mid] == 2)
swap(nums[mid], nums[high--]);
else ++mid;
}
}
};
279. Perfect Squares
Given a positive integer n, find the least number of perfect square numbers (for example,
1, 4, 9, 16, ...) which sum to n.Example 1:
Input: n = 12 Output: 3 Explanation: 12 = 4 + 4 + 4.Example 2:
Input: n = 13 Output: 2 Explanation: 13 = 4 + 9.
这是一个多重背包问题。可以放入背包的物品为1 4 9 ...等所有不大于n的平方数。每个物品可以放入背包无限次。令dp[i][v]为用前i件物品填满大小为v的背包的方法数,则其转移方程为dp[i][v] = min(dp[i-1][v], dp[i][v-nums[i]] + 1),即要么第i件物品一件不放,要么至少放入一件。多重背包的做法效率好像不是很好,在讨论区有其他的动态规划视角回答,不过这些回答并没有多重背包解法普适。
class Solution {
public:
int numSquares(int n) {
vector<int> nums;
for (int i = 1, ii; ; ++i) {
ii = i * i;
if (ii < n) nums.push_back(ii);
else if (ii == n) return 1;
else break;
}
vector<int> dp(n+1, 0x7fffffff);
dp[0] = 0;
for (int i = 0; i < nums.size(); ++i) {
for (int v = nums[i]; v <= n; ++v) {
dp[v] = std::min(dp[v], dp[v-nums[i]] + 1);
}
}
return dp[n];
}
};
208. Implement Trie (Prefix Tree)
Implement a trie with
insert,search, andstartsWithmethods.Example:
Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // returns true trie.search("app"); // returns false trie.startsWith("app"); // returns true trie.insert("app"); trie.search("app"); // returns true
Trie树是一种多叉树,存储的每一个单词都对应着树中一条根节点->叶子节点的路径。更多Trie树相关信息请看这里。我用了一个哈希表来存储节点的孩子。由于题目中的字符范围只在a~z之间,所以也可以用一个长度为26的数组来保存孩子。
class Trie {
struct node {
char val;
bool leaf;
unordered_map<char, node*> children;
node(char val) : val(val), leaf(false) {}
};
node *root;
public:
/** Initialize your data structure here. */
Trie() {
root = new node(' ');
}
/** Inserts a word into the trie. */
void insert(string word) {
node *curr = root;
for (char c : word) {
if (!curr->children.count(c))
curr->children[c] = new node(c);
curr = curr->children[c];
}
curr->leaf = true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
node *curr = root;
for (char c : word) {
if (!curr->children.count(c)) return false;
curr = curr->children[c];
}
return curr->leaf;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
node *curr = root;
for (char c : prefix) {
if (!curr->children.count(c)) return false;
curr = curr->children[c];
}
return true;
}
};
128. Longest Consecutive Sequence
Given an unsorted array of integers, find the length of the longest consecutive elements sequence.
Your algorithm should run in O(n) complexity.
Example:
Input: [100, 4, 200, 1, 3, 2] Output: 4 Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.
这道题我之前的做法是,使用一个哈希表来把连续序列的首尾元素映射到它们所在序列的长度。序列除首尾元素外的元素的映射值未定义。对于正在访问的元素i,如果它已经在哈希表里了,那么它对增加序列长度没有意义,直接忽视它即可。如果i-1和i+1都不在哈希表里,说明它是一个孤立的值,它自己构成一个长度为1的序列。如果i-1在哈希表里而i+1不在哈希表里,说明i应该是一个序列的首部(即序列中最大的元素),可以通过my_map[i-1]获得该序列的长度,然后将加上i之后的序列长度填入my_map[i]。注意序列的尾部元素的映射值也要修改。由于序列原先长my_map[i-1],那么序列尾部元素就是i-my_map[i-1]。将尾部元素的映射值也改成新长度my_map[i]。如果i+1在哈希表里而i-1不在哈希表里,同理,这时i是一个序列的尾部。如果i+1和i-1都在哈希表里,那么i可以连接两个已存在的序列。通过i-my_map[i-1]和i+my_map[i+1]定位后面序列的尾部和前面序列的首部,将这两个元素的映射值改为两个序列合并后的长度即可。
这种方法时间复杂度虽然是O(n),但代码写起来繁琐,过程复杂,不如这个大神写的。同样是O(n),我的就显得很挫,他的就显得很高端……
class Solution {
public:
// only two ends of a consecutive sequence would have a certain map value
int longestConsecutive(vector<int> &num) {
unordered_map<int, int> my_map;
int rtn = 0;
for (auto &i: num) {
// duplicate value
if (my_map[i] != 0) continue;
// isolated value
else if (my_map[i+1] == 0 && my_map[i-1] == 0) my_map[i] = 1;
// head of a sequence
else if (my_map[i+1] == 0 && my_map[i-1] != 0) my_map[i] = my_map[i-1]+1, my_map[i-my_map[i-1]] = my_map[i];
// tail of a sequence
else if (my_map[i+1] != 0 && my_map[i-1] == 0) my_map[i] = my_map[i+1]+1, my_map[i+my_map[i+1]] = my_map[i];
// link two unconected sequences
else my_map[i] = my_map[i-my_map[i-1]] =my_map[i+my_map[i+1]] = my_map[i-my_map[i-1]] + my_map[i+my_map[i+1]] + 1;
if (my_map[i] > rtn) rtn = my_map[i];
}
return rtn;
}
};
// 别人的做法
class Solution {
public:
int longestConsecutive(vector<int> &num) {
set<int> s;
for (int n : num) s.insert(n);
int best = 0, y;
for (int x : num) {
// x is the tail of a sequence
if (s.find(x-1) == s.end()) {
y = x + 1; // get length of the sequence
while (s.find(y) != s.end()) ++y;
best = max(best, y - x);
}
}
return best;
}
};
560. Subarray Sum Equals K
Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
Input:nums = [1,1,1], k = 2 Output: 2
要计算sum(nums[i:j]),可以通过sum(nums[:j]) - sum(nums[:i])得到。在顺序遍历nums的同时,记录之前见过的前缀和的个数。假设当前访问的下标是i,之前每有一个前缀和为sum(nums[;i+1]) - k,就会有一个序列nums[j:i+1],它的和为k。可以用哈希表存储之前的前缀和,这样时间复杂度仅为O(n)。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> m;
m[0] = 1;
int sum_ = 0, rtn = 0;
for (int n : nums) {
sum_ += n;
rtn += m[sum_ - k];
++m[sum_];
}
return rtn;
}
};
236. Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
这题我做的不好,我的代码太过冗余,不如来看这个回答:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root || root == p || root == q) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
return !left ? right : !right ? left : root;
}
如果!root,那么返回root,即nullptr。从example2中可以看出,在以5为根节点的子树上搜索5 4的LCA,假如LCA在这个子树上,且根刚好等于p,那么LCA必定是根节点。因此,如果root == p或者root == q,那么直接返回根节点即可。就算LCA不在该子树上,在该子树上搜索返回一个非空节点,也能告诉父节点们,这棵子树上存在要找的p q中的一个。如果root不等于p q,便递归地搜索左子树和右子树。代码第四行比较乱,它在left和right都非空的时候返回root,其他时候返回left和right中非空的那一个。如果两个都为空,则返回nullptr。因此,如果左右子树中包含p q的某一个,那么返回值肯定是非空的,向它的父节点通告它包含p q的某一个。如果left right都为非空,说明左右子树各包含p q中的一个。这种情况下,root就是LCA,返回root。该节点的祖先节点在计算left right时,肯定有一个是非空(就是那个LCA),另一个是空(因为p q都不在另一边子树上)。所以祖先节点们的返回值就是LCA。最终整棵树的根节点返回LCA,圆满结束。
155. Min Stack
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
- push(x) – Push element x onto stack.
- pop() – Removes the element on top of the stack.
- top() – Get the top element.
- getMin() – Retrieve the minimum element in the stack.
Example:
MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> Returns -3. minStack.pop(); minStack.top(); --> Returns 0. minStack.getMin(); --> Returns -2.
用一个变量min_来记录当前栈中的最小值。当push进一个比min_更小的数时,将min_先push进栈中,再将数push进去,并修改min_为新的最小值。在pop元素时,如果被pop元素等于min_,说明栈中最小值会发生变动,变为 在被pop元素之前push进去的元素的最小值。这个最小值早已保存在栈中。再对栈pop一次就可以得到。
可以看出,最小值们也有LIFO的特点。所以,也可以用一个另外的栈来保存这些最小值。当这个最小值栈的栈顶元素等于当前被pop元素,最小值也应该更新,将最小值栈pop掉一个元素获得上一个最小值。不过这个最小值栈是比较多余的,完全可以和原有栈合二为一。
class MinStack {
int min_;
vector<int> arr;
public:
/** initialize your data structure here. */
MinStack() : min_(0x7fffffff) {}
void push(int x) {
if (x <= min_) {
arr.push_back(min_);
min_ = x;
}
arr.push_back(x);
}
void pop() {
int top = arr.back();
arr.pop_back();
if (top == min_) {
min_ = arr.back();
arr.pop_back();
}
}
int top() {
return arr.back();
}
int getMin() {
return min_;
}
};
416. Partition Equal Subset Sum
Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
Example 1:
Input: [1, 5, 11, 5] Output: true Explanation: The array can be partitioned as [1, 5, 5] and [11].Example 2:
Input: [1, 2, 3, 5] Output: false Explanation: The array cannot be partitioned into equal sum subsets.
这道题其实就是一个01背包问题,要求在数组中挑出若干个数,使其和为数组和sum的二分之一,等价于从物品中挑选出若干物品填满一个大小为sum/2的背包。令dp[i][j]表示用前i件物品,是否能填满一个大小为j的背包。转移公式为dp[i][j] = dp[i-1][j] || dp[i-1][j-arr[i]],即如果能用前i-1件物品填满j大小的背包,或者j-arr[i]大小的背包,就能用前i件物品填满j大小的背包。
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum_ = accumulate(nums.begin(), nums.end(), 0);
if (sum_ % 2 == 1) return false; // should be even
sum_ = sum_ / 2;
vector<bool> dp(sum_+1, false);
dp[0] = true; // for convenience
for (int i = 0; i < nums.size(); ++i) {
for (int j = sum_; j >= nums[i]; --j)
dp[j] = dp[j] || dp[j-nums[i]];
}
return dp[sum_];
}
};
由于这道题的dp数组元素只要一个比特,所以可以用一个bitset来代替vector数组。用bitset还有一个好处,就是内层循环for (int j = sum_; ...)不需要真的去遍历了,只需要对bitset做位移操作即可,dp[j-nums[i]]相当于dp << nums[i]。具体地操作请看代码:
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum_ = accumulate(nums.begin(), nums.end(), 0);
if (sum_ % 2 == 1) return false; // should be even
sum_ = sum_ / 2;
const int MAX_NUM = 100;
const int MAX_ARRAY_SIZE = 200;
// sum_ <= MAX_NUM * MAX_ARRAY_SIZE / 2
bitset<MAX_NUM * MAX_ARRAY_SIZE / 2 + 1> dp(1);
for (int n: nums)
dp |= dp << n;
return dp[sum_];
}
};
240. Search a 2D Matrix II
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]
这道题的算法复杂度可以降低到O(m+n)(分别是二维数组的长和宽)。通过观察下面的图:
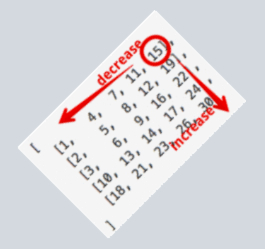
可以发现,如果我们从二维数组右上角的点开始,设当前点为array[x][y],如果array[x][y] < target,那么array[x][:y]这些元素,都会小于target。我们可以将当前点移动到array[x+1][y]表示将这部分元素舍弃。如果array[x][y] > target,则array[x+1:][y]的元素都会大于target。同理,我们将当前点移动到array[x][y-1],表示将这些元素舍弃。如果当前点走到了边界,依然没有碰到一个点是等于target的,说明二维数组里没有元素和target相等。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.empty() || matrix[0].empty()) return false;
int x = 0, y = matrix[0].size() - 1;
while (x < matrix.size() && y >= 0) {
if (matrix[x][y] == target) return true;
else if (matrix[x][y] < target) ++x;
else --y;
}
return false;
}
};
301. Remove Invalid Parentheses
Remove the minimum number of invalid parentheses in order to make the input string valid. Return all possible results.
Note: The input string may contain letters other than the parentheses
(and).Example 1:
Input: "()())()" Output: ["()()()", "(())()"]Example 2:
Input: "(a)())()" Output: ["(a)()()", "(a())()"]Example 3:
Input: ")(" Output: [""]
It is easy to find the length of the longest subsequence by counting the number of invalid left and right parentheses in the string. We denote the numbers with left and right. The minimum number of invalid parentheses to remove is left+right. Then we search all possible valid subsequences by backtracking. We can prone the recursion by some limits:
- the number of removed ‘(‘ or ‘)’ must be
leftorright - num of ‘)’ in the prefix of the subsequence could not be larger than num of ‘(‘
class Solution:
def removeInvalidParentheses(self, s):
# first check how many '(' and ')' will be removed to get a longest subsequence
left, right = 0, 0 # num of invalid left and right parentheses
for char in s:
if char == '(':
left += 1
elif char == ')':
if left == 0: # an invalid ')'
right += 1
else:
left -= 1
# the length of any longest subsequence would be len(s)-left-right
ans = set()
def recurse(subseq, idx, rem_left, rem_right, count_left, count_right):
"""
backtracking.
:param subseq: generated substring from s[:idx]
:param idx: considering s[idx]
:param rem_left: rem_left/rem_right are initialized with left/right.
They means how many '(' or ')' can be dropped
:param rem_right:
:param count_left: how many '(' or ')' in subseq
:param count_right:
:return: None
"""
if idx == len(s):
if rem_left == 0 and rem_right == 0:
# a valid answer
ans.add(subseq)
return
# if s[idx] is '(' or ')', we try to drop it
if s[idx] == '(' and rem_left > 0:
recurse(subseq, idx+1, rem_left-1, rem_right, count_left, count_right)
elif s[idx] == ')' and rem_right > 0:
recurse(subseq, idx+1, rem_left, rem_right-1, count_left, count_right)
# otherwise, we add it into subseq, making sure that subseq is 'right' valid
# which means, ')' must be less than '(' in subseq
if s[idx] == '(':
recurse(subseq+'(', idx+1, rem_left, rem_right, count_left+1, count_right)
elif s[idx] == ')':
if count_right < count_left:
recurse(subseq+')', idx+1, rem_left, rem_right, count_left, count_right+1)
else:
# s[idx] is other characters.
recurse(subseq+s[idx], idx+1, rem_left, rem_right, count_left, count_right)
recurse('', 0, left, right, 0, 0)
if len(ans) == 0:
return [""]
return list(ans)
300. Longest Increasing Subsequence
Given an unsorted array of integers, find the length of longest increasing subsequence.
Example:
Input: [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
这道题可以用动态规划解决。令dp[j]为以第j个元素结尾的子序列的最长长度。对于一个i > j,如果有nums[i] > nums[j],那么dp[i] >= dp[j] + 1。这种方法的时间复杂度为O(n^2),在讨论区里有人提出多种O(nlgn)的方法。最容易懂的一种表达方式是维护一个有序队列res。对于当前遍历的元素i,如果它大于res中所有的元素,则将它添加到res尾部。如果它只大于一部分元素,则找到它的位置(位置之前的元素都小于它),然后将位置上的旧元素替换成它。我们可以把res[j]看作是长度为j+1的(可以在后继续接龙的)子序列的最小尾部元素。如果当前元素i比res[res.size()-1]还大,说明能构成一个res.size()+1长度的序列,LIS长度更新。如果i并没有比res[res.size()-1]大,而是比res其他某个元素大,就用i代替它。
[1,2,7,8,3,4,5,9,0]
1 -> [1]
2 -> [1,2]
7 -> [1,2,7]
8 -> [1,2,7,8]
3 -> [1,2,3,8] // we replaced 7 with 3, since for the longest sequence we need only the last number and 1,2,3 is our new shorter sequence
4 -> [1,2,3,4] // we replaced 8 with 4, since the max len is the same but 4 has more chances for longer sequence
5 -> [1,2,3,4,5]
9 -> [1,2,3,4,5,9]
0 -> [0,2,3,4,5,9] // we replaced 1 with 0, so that it can become a new sequence
// O(n^2)
class Solution {
public:
// dp[i] == length of the longest LIS ends at nums[i]
int lengthOfLIS(vector<int>& nums) {
if (nums.empty()) return 0;
int size = nums.size(), max_len = 1;
vector<int> dp(size, 1);
for (int i = 1; i < size; ++i) {
for (int j = i-1; j >= 0; --j) {
if (nums[i] > nums[j] && dp[j]+1 > dp[i]) dp[i] = dp[j] + 1;
}
if (max_len < dp[i]) max_len = dp[i];
}
return max_len;
}
};
// O(nlgn)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> res;
for(int i=0; i<nums.size(); i++) {
// binary search. O(lgn)
auto it = std::lower_bound(res.begin(), res.end(), nums[i]);
if(it==res.end()) res.push_back(nums[i]);
else *it = nums[i];
}
return res.size();
}
};
295. Find Median from Data Stream
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
For example,
[2,3,4]`, the median is `3 [2,3]`, the median is `(2 + 3) / 2 = 2.5Design a data structure that supports the following two operations:
- void addNum(int num) - Add a integer number from the data stream to the data structure.
- double findMedian() - Return the median of all elements so far.
Example:
addNum(1) addNum(2) findMedian() -> 1.5 addNum(3) findMedian() -> 2
这道题我想不出来,因此解释一下此人的答案:
首先准备一个最大堆small,一个最小堆large,其中small装所有数中最小的floor(n/2)个数,而large装最大的ceil(n/2)个数。显然,如果small的元素个数大于large的元素个数,那么中值会是small.top(),因为这个数是第floor(n/2)大的数。如果small的元素个数等于large的元素个数,那么small.top()和large.top()的平均值就是中值。在每次addNum时,必须维持small和large的性质。维持的方法是:将新添加数num先添加进small里。这时可能会因为添加了num,small变得可能有元素比large的元素大了。所以要将small的最大值传给large,以保证large的元素都不比small的小。但是这样的话,large的元素个数可能会比small的元素个数多。所以要做一次检查,如果large的元素个数比small的元素个数多,就将large最小的元素传给small。最后large和small重新符合它们的定义。
class MedianFinder {
priority_queue<long> small, large;
public:
/** initialize your data structure here. */
MedianFinder() { }
void addNum(int num) {
small.push(num);
large.push(-small.top());
small.pop();
if (small.size() < large.size()) {
small.push(-large.top());
large.pop();
}
}
double findMedian() {
if (large.size() < small.size()) return small.top();
return (double) (-large.top() + small.top()) / 2;
}
};
72. Edit Distance
Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.
You have the following 3 operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
Example 1:
Input: word1 = "horse", word2 = "ros" Output: 3 Explanation: horse -> rorse (replace 'h' with 'r') rorse -> rose (remove 'r') rose -> ros (remove 'e')Example 2:
Input: word1 = "intention", word2 = "execution" Output: 5 Explanation: intention -> inention (remove 't') inention -> enention (replace 'i' with 'e') enention -> exention (replace 'n' with 'x') exention -> exection (replace 'n' with 'c') exection -> execution (insert 'u')
这个动态规划的递推式要想出来还是比较简单的。首先,令dp[i][j]为将word1[:i]和word2[:j]变成同样字符串所需的最小步数。根据和维特比算法类似的思路,可以看出:
- 如果
word1[i-1]和word2[j-1]相同,那么dp[i][j]=dp[i-1][j-1](否则,dp[i-1][j-1]不是word1[:i-1]和word2[:j-1]之间的最短距离。这是维特比算法的思路。之后不再解释) - 或者可以给
word1[:i-1]后面加个word2[j-1],则dp[i][j] = dp[i][j-1] + 1;或者给把word1[i-1]删掉(跟给word2后面加个word1[i-1]是一样效果),则dp[i][j] = dp[i-1][j] + 1;或者把word1[i-1]替换成word2[j-1],那么dp[i][j] = dp[i-1][j-1] + 1。
综上,时间复杂度为$O(mn)$,$m, n$为两个字符串的长度。
def minDistance(self, word1: str, word2: str) -> int:
# dynamic programming
# dis[i][j] = min distance between word1[:i] and word2[:j]
# focus on (i-1)th word of word1 and (j-1)th word2(denoted by c and d)
# 1. if replace c -> d: dis[i][j] == dis[i-1][j-1] + 1
# 2. add a d to word1: dis[i][j] == dis[i][j-1] + 1
# 3. delete c: dis[i][j] == dis[i-1][j] + 1
# 4. c == d: dis[i][j] == dis[i-1][j-1]
dp = [[0 for _ in range(len(word2)+1)] for _ in range(len(word1)+1)]
# initialize
for i in range(len(word1)+1):
dp[i][0] = i
for j in range(len(word2)+1):
dp[0][j] = j
for i in range(1, len(word1)+1):
for j in range(1, len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
return dp[-1][-1]
239. Sliding Window Maximum
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.
Follow up: Could you solve it in linear time?
Example:
Input: nums = [1,3,-1,-3,5,3,6,7], and k = 3 Output: [3,3,5,5,6,7] Explanation: Window position Max --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
使用一个双向队列,存储当前窗口内可能成为最大值的元素的下标。所谓可能成为最大值的元素,必须符合以下任一条件:
- 在窗口内没有其他元素比它大。
- 仅有它前面有元素比它大。在窗口滑动到前面的元素都被移出窗口后,这个元素可能成为窗口内最大的元素。
显然,这个双向队列可以以以下的方法构造和维护:对当前元素nums[i],如果双向队列的尾端元素比它小,那么需要将尾端元素移除,因为直到这个尾端元素被移出窗口,它都不可能成为窗口内最大值了(永远败给nums[i](⊙︿⊙))。这个步骤需要循环进行,直到队列为空或者尾端元素比nums[i]大。此外,由于窗口的滑动,如果队列首端的元素已经离开窗口,需要将该元素一并从队列中移除。如此就能保证双向队列的首端元素在窗口内,且是队列内元素的最大值,即是当前窗口最大值。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int> q;
int i = 0;
for ( ; i < k; ++i) {
while (!q.empty() && nums[q.back()] <= nums[i]) q.pop_back();
q.push_back(i);
}
vector<int> rtn = {nums[q.front()]};
for ( ; i < nums.size(); ++i) {
while (!q.empty() && nums[q.back()] <= nums[i]) q.pop_back();
q.push_back(i);
if (q.front() + k <= i) q.pop_front();
rtn.push_back(nums[q.front()]);
}
return rtn;
}
};
207.210.630. Course Schedule & II & III
There are a total of
numCoursescourses you have to take, labeled from0tonumCourses-1.Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair:
[0,1]Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]] Output: true Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.Example 2:
Input: numCourses = 2, prerequisites = [[1,0],[0,1]] Output: false Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
这道题其实就是在有向图中寻找是否有环路。寻找环路用DFS或者BFS都行。使用一个数组color标记节点是否访问过,如果值为:
- 0,未曾访问过。
- -1,有路径可以到达当前正在被访问的节点。
- 1,已经访问过,没有路径到达当前正在被访问的节点。
class Solution {
bool dfs(int i, vector<int> &color, vector<vector<int>>& adjecent) {
color[i] = -1;
for (int c : adjecent[i]) {
if (color[c] == -1) return false;
if (color[c]) continue;
if (!dfs(c, color, adjecent)) return false;
}
color[i] = 1;
return true;
}
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> color(numCourses, 0);
vector<vector<int>> adjecent(numCourses, vector<int>());
for (vector<int> &pre: prerequisites) adjecent[pre[0]].push_back(pre[1]);
for (int i = 0; i < numCourses; ++i) {
if (!color[i]) {
if (!dfs(i, color, adjecent)) return false;
}
}
return true;
}
};
There are a total of n courses you have to take, labeled from
0ton-1.Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair:
[0,1]Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses.
There may be multiple correct orders, you just need to return one of them. If it is impossible to finish all courses, return an empty array.
Example 1:
Input: 2, [[1,0]] Output: [0,1] Explanation: There are a total of 2 courses to take. To take course 1 you should have finished course 0. So the correct course order is [0,1] .Example 2:
Input: 4, [[1,0],[2,0],[3,1],[3,2]] Output: [0,1,2,3] or [0,2,1,3] Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3] .
这道题是拓扑排序题。和上面的寻找环路一样都非常常规。使用一个数组adjecent来记录课程的限制条件。例如,如果课程0限制课程1,那么1会被添加进adjecent[0]中。使用另一个数组indegrees来记录每个节点的入度。拓扑排序的思路是:
- 输出所有入度为0的点。输出后,将其从图上移除,调整剩下节点的入度。
- 不断循环第一步,直到所有节点被输出。
如果图中存在环路,那么输出的序列元素个数会比总节点个数少,因为环路上的点找不到一个入度为0的点作为入口,以供DFS进入。
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> color(numCourses, 0);
vector<vector<int>> adjecent(numCourses, vector<int>());
vector<int> indegrees(numCourses, 0);
for (vector<int> &pre: prerequisites) {
adjecent[pre[1]].push_back(pre[0]);
++indegrees[pre[0]];
}
vector<int> rtn;
queue<int> head;
for (int i = 0; i < numCourses; ++i) {
if (!indegrees[i]) head.push(i);
}
while (head.size()) {
int curr = head.front();
rtn.push_back(curr);
head.pop();
for (int n : adjecent[curr]) {
if (--indegrees[n] == 0) head.push(n);
}
}
if (rtn.size() == numCourses) return rtn;
return {};
}
};
There are
ndifferent online courses numbered from1ton. Each course has some duration(course length)tand closed ondthday. A course should be taken continuously fortdays and must be finished before or on thedthday. You will start at the1stday.Given
nonline courses represented by pairs(t,d), your task is to find the maximal number of courses that can be taken.Example:
Input: [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]] Output: 3 Explanation: There're totally 4 courses, but you can take 3 courses at most: First, take the 1st course, it costs 100 days so you will finish it on the 100th day, and ready to take the next course on the 101st day. Second, take the 3rd course, it costs 1000 days so you will finish it on the 1100th day, and ready to take the next course on the 1101st day. Third, take the 2nd course, it costs 200 days so you will finish it on the 1300th day. The 4th course cannot be taken now, since you will finish it on the 3300th day, which exceeds the closed date.
这道题和I II并没有什么联系……第一眼看它,就觉得它是一个01背包问题。设所有课程中closed date最大值为max_date。这道题实际上就是要求填充大小为max_date的背包,最多能放多少件物品。duration是物品的体积,close date限定了它们至多能放在多大的背包里。转移公式如下:
dp{i][v] = max{dp[i-1][v], dp[i-1][v-t]+1};
事先将课程按closed date从小到大排序,以及内层循环中反向迭代v,以及fill操作,是为了减少计算量。然而,由于这种DP解法的复杂度依旧为O(VN),提交以后便超时了……在LeetCode讨论区中,出现得最多的是优先队列的做法。优先队列的做法和01背包问题的做法有异曲同工之妙。假设dp[i]是将courses[:i]放入大小为max_date的背包中,能放入的最大物品数,cum为放入物品的体积和。对于courses[i],如果cum+courses[i][0] <= courses[i][1],说明能够将courses[i]也放入背包中,dp[i+1]=dp[i] + 1。如果cum+courses[i][0] > courses[i][1],那么有两种可能:
- 放弃将
courses[i]放入背包中。那么dp[i+1] = dp[i],cum也不会变。 - 将原背包中一个物品取出,再将
courses[i]放入,前提是体积和不超过courses[i]的closed date。在这种情况下,依旧有dp[i+1] = dp[i],但是cum改变了。为了方便之后放更多物品(贪心算法思想),应该将背包内最大的物品移除,换成courses[i],以减小cum。
// 0-1 knapsack
class Solution {
public:
int scheduleCourse(vector<vector<int>>& courses) {
// dp{i][v] = max{dp[i-1][v], dp[i-1][v-t]+1}
sort(courses.begin(), courses.end(), [](vector<int> &x, vector<int> &y) { return x[1] < y[1]; });
int max_date = courses.back()[1];
vector<int> dp(max_date+1, 0);
for (int i = 0; i < courses.size(); ++i) {
for (int v = courses[i][1]; v >= courses[i][0]; --v) {
dp[v] = max(dp[v], dp[v-courses[i][0]]+1);
}
fill(dp.begin()+courses[i][1]+1, dp.end(), dp[courses[i][1]]);
}
return dp[max_date];
}
};
// priority queue
class Solution {
public:
int scheduleCourse(vector<vector<int>>& courses) {
priority_queue<int> q;
int cum = 0;
sort(courses.begin(), courses.end(), [](vector<int> &x, vector<int> &y) { return x[1] < y[1]; });
for (int i = 0; i < courses.size(); ++i) {
if (cum + courses[i][0] <= courses[i][1]) {
cum += courses[i][0];
q.push(courses[i][0]);
} else if (!q.empty() && courses[i][0] < q.top()) {
cum = cum - q.top() + courses[i][0];
q.pop();
q.push(courses[i][0]);
}
}
return q.size();
}
};
148. Sort List
Sort a linked list in O(n log n) time using constant space complexity.
Example 1:
Input: 4->2->1->3 Output: 1->2->3->4Example 2:
Input: -1->5->3->4->0 Output: -1->0->3->4->5
由于列表只支持单向访问,所以适合使用一个尽可能对其他类型访问无需求的排序算法来排序列表。我使用的是归并排序。归并排序只在将列表分治为两段时需要迭代找到中点,其他时候顺其自然地单向迭代即可。
class Solution {
public:
ListNode* sortList(ListNode* head) {
// merge sort
if (!head || !head->next) return head;
ListNode *slow = head, *fast = head;
// find the median node
while (fast && fast->next && fast->next->next) slow = slow->next, fast = fast->next->next;
ListNode *right = slow->next;
slow->next = nullptr;
// divide
head = sortList(head), right = sortList(right);
// merge
ListNode *vhead = new ListNode(0), *curr = vhead;
while (head && right) {
if (head->val < right->val) curr->next = head, head = head->next;
else curr->next = right, right = right->next;
curr = curr->next;
}
if (head) curr->next = head;
if (right) curr->next = right;
head = vhead->next;
delete vhead;
return head;
}
};
141.142 Linked List Cycle & II
Given a linked list, determine if it has a cycle in it.
To represent a cycle in the given linked list, we use an integer
poswhich represents the position (0-indexed) in the linked list where tail connects to. Ifposis-1, then there is no cycle in the linked list.Example 1:
Input: head = [3,2,0,-4], pos = 1 Output: true Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
Input: head = [1,2], pos = 0 Output: true Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:
Input: head = [1], pos = -1 Output: false Explanation: There is no cycle in the linked list.
在链表中检测环路最经典的做法就是快慢指针。快慢指针还可以寻找环路的入口,具体证明如下:
-
首先,如果链表中存在环路,那么快慢指针一定会相聚于环中。这是因为当他们进入环路以后,快指针和慢指针的相对速度为1,每次快指针相对于慢指针的距离会减少1,所以迟早会走到一起。
-
假设链表起点到环路入口距离为
x,环路入口到两个指针相聚的地方距离为y,相聚地方到环路入口距离为z,环路长度为r = y + z。当两个指针相聚时,假设快指针比慢指针多走了d圈,那么有这是因为快指针走的距离是慢指针走的距离的两倍。这个式子可以化简得到
然后用另一个慢指针从链表起点出发,和第一个慢指针一起行走,它们相遇的地方就是环路入口。这是因为,当第二个慢指针走完
x距离时,第一个慢指针离它开始的地方(和快指针的相遇处)的距离为z,即处于环路入口。两个慢指针因此刚好相聚于环路入口。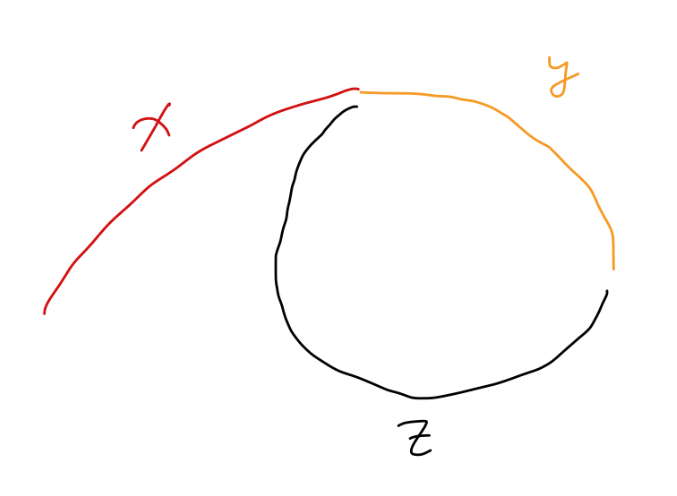
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while (fast && fast->next) {
fast = fast->next->next, slow = slow->next;
if (fast == slow) return true;
}
return false;
}
};
Given a linked list, return the node where the cycle begins. If there is no cycle, return
null.
寻找环路入口,思路上面已经解释。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while (fast && fast->next) {
fast = fast->next->next, slow = slow->next;
if (fast == slow) {
fast = head;
while (fast != slow)
fast = fast->next, slow = slow->next;
return slow;
}
}
return nullptr;
}
};
23. Merge k Sorted Lists
Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.
Example:
Input: [ 1->4->5, 1->3->4, 2->6 ] Output: 1->1->2->3->4->4->5->6
使用一个优先队列(最小堆)来保存所有链表的头部节点。每次从队列中弹出具有最小值的节点,并将它的后继添加进队列,直到优先队列为空。
struct cmp {
bool operator() (ListNode *p1, ListNode *p2) {
return p1->val > p2->val;
}
};
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *vhead = new ListNode(0), *curr = vhead;
priority_queue<ListNode*, vector<ListNode*>, cmp> pq;
for (ListNode *p : lists) {
if (p) pq.push(p);
}
while (pq.size()) {
ListNode *min = pq.top();
pq.pop();
if (min->next) pq.push(min->next);
curr->next = min, curr = curr->next;
}
curr = vhead->next;
delete vhead;
return curr;
}
};
139. Word Break
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.
Note:
- The same word in the dictionary may be reused multiple times in the segmentation.
- You may assume the dictionary does not contain duplicate words.
Example 1:
Input: s = "leetcode", wordDict = ["leet", "code"] Output: true Explanation: Return true because "leetcode" can be segmented as "leet code".Example 2:
Input: s = "applepenapple", wordDict = ["apple", "pen"] Output: true Explanation: Return true because "applepenapple" can be segmented as "apple pen apple". Note that you are allowed to reuse a dictionary word.Example 3:
Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] Output: false
这道题可以用动态规划解决。令dp[i]表示s[0:i]是否可以被字典中单词分割。对于s[0:i],假设字典中有一个单词和它的后缀匹配,并且在去掉这个后缀后(假设长度为w),有dp[i-w] == true,那么说明s[0:i]能被字典分割。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
if (s.length() == 0) return false;
int len = s.length();
vector<bool> dp(len+1, false);
dp[0] = true;
for (int i = 1; i <= len; ++i) {
for (string &word : wordDict) {
if (word.length() <= i && dp[i-word.length()] && s.substr(i-word.length(), word.length()) == word) {
dp[i] = true;
break;
}
}
}
return dp[len];
}
};
160. Intersection of Two Linked Lists
Write a program to find the node at which the intersection of two singly linked lists begins.
For example, the following two linked lists:
begin to intersect at node c1.
Example 1:
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 Output: Reference of the node with value = 8 Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.Example 2:
Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 Output: Reference of the node with value = 2 Input Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [0,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.Example 3:
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 Output: null Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values. Explanation: The two lists do not intersect, so return null.
我一开始想到的做法是将链表A的首尾连接起来,这样如果A和B相交,则交点构成环路A的入口。使用LeetCode 141的环路检测方法,就能探测到那个入口点。题目要求链表结构不能改变,只需要在找到入口点后将链表A的首尾相连取消即可。这种方法可行,但是不够优雅,评论区第一的方法明显更好:假设链表A起点到交点的距离为x,链表B起点到交点的距离为y,交点到共同的末端节点距离为z。用两个指针a b,分别从A起点和B起点开始走。在a走到链表末端就跳到B起点,在b走到链表末端就跳到A起点。如果链表有交点,那么a b一定会相聚于那个交点。这是因为:
x == y的情况,显然。x != y。在两个节点走动距离为x + y + z时,它们都会到达交点,并在那里相聚。由于x != y,在此之前它们不会相聚。
代码如下。注意在链表没有交点时,两个节点至多在走完两段链表后,会同时为nullptr。这时,可以确定两个链表没有交点。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (!headA || !headB) return nullptr;
ListNode *a = headA, *b = headB;
while (a != b) {
if (!a) a = headB;
else a = a->next;
if (!b) b = headA;
else b = b->next;
}
return a;
}
};
234. Palindrome Linked List
Given a singly linked list, determine if it is a palindrome.
Example 1:
Input: 1->2 Output: falseExample 2:
Input: 1->2->2->1 Output: true
找到链表的中点,将其划分为两部分。将其中一部分翻转,比较两部分是否一样,如果一样则为回文。
这位大神将找中点和翻转的步骤合在一起了,非常巧妙。甚至提供了一种将翻转链表复原的解法,非常秀……
class Solution {
public:
bool isPalindrome(ListNode* head) {
if (!head) return true;
ListNode *fast = head, *slow = head, *prev = nullptr, *next = head->next;
while (fast && fast->next) {
fast = fast->next->next;
// reverse list when finding median
slow->next = prev, prev = slow, slow = next, next = next->next;
}
// prev and slow are heads of the left and right lists
if (fast) slow = slow->next;
while (prev && slow) {
if (prev->val != slow->val) return false;
prev = prev->next, slow = slow->next;
}
return true;
}
};
56. Merge Intervals
Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].Example 2:
Input: [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.
为了方便考虑,先将所有间隔按起始点从小到大排序。这样就不用担心后面的间隔会包含前面的间隔的情况。假设当前添加进结果集rtn的最后一个间隔的起始点和结束点分别为p m,下一个待访问的间隔的起始点和结束点为a b,分情况考虑它们的关系:
p <= m < a <= b:显然,间隔a b是要被添加进结果集的,因为它并不和现有间隔有交集。p <= a <= m <= b或p <= m <= a <= b:间隔a b有一部分和间隔p m覆盖。这种情况下,这两个间隔会合并为一个更大的间隔p b,因此应该将rtn中最后一个间隔修改为p b。p <= a <= b <= m:间隔a b被包含在间隔p m中。这时,间隔a b是没有用的,可以被忽略。
根据以上这三种情况,依次将各个间隔添加进rtn中:
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end(),
[](vector<int> &x, vector<int> &y) { return x[0] < y[0]; });
vector<vector<int>> rtn;
for (vector<int> &intv: intervals) {
if (rtn.empty()) {
rtn.push_back(intv);
} else if (rtn.back()[1] < intv[0]) rtn.push_back(intv); // m < a
else if (intv[1] <= rtn.back()[1]) continue; // b <= m
else rtn.back()[1] = intv[1];
}
return rtn;
}
};
20. Valid Parentheses
Given a string containing just the characters
'(',')','{','}','['and']', determine if the input string is valid.An input string is valid if:
- Open brackets must be closed by the same type of brackets.
- Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
Example 1:
Input: "()" Output: trueExample 2:
Input: "()[]{}" Output: trueExample 3:
Input: "(]" Output: falseExample 4:
Input: "([)]" Output: falseExample 5:
Input: "{[]}" Output: true
非常容易的括号匹配题。绝大多数括号匹配题都可以用栈解决。
class Solution {
public:
bool isValid(string s) {
std::stack<char> st;
for (char c: s) {
if (c == '(' || c == '{' || c == '[') st.push(c);
else if (c == ')' && !st.empty() && st.top() == '(') st.pop();
else if (c == '}' && !st.empty() && st.top() == '{') st.pop();
else if (c == ']' && !st.empty() && st.top() == '[') st.pop();
else return false;
}
return st.empty();
}
};
221. Maximal Square
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
Example:
Input: 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 Output: 4
这是一道动态规划题。令dp[i][j]为以matrix[i][j]为右下角顶点的正方形的最大边长。显然,dp[i][j]受dp[i-1][j], dp[i][j-1], dp[i-1][j-1]的限制。通过画图可以发现,以matrix[i-1][j-1]为右下角顶点的正方形占据以matrix[i][j]为右下角顶点的正方形的绝大部分,显然dp[i][j]不能超过dp[i-1][j-1] + 1。其次,以matrix[i-1][j]为右下角顶点的正方形和以matrix[i][j-1]为右下角顶点的正方形为以matrix[i][j]为右下角顶点的正方形提供右侧边和底部边,dp[i][j]同样也不能超过dp[i-1][j] + 1和dp[i][j-1] + 1。因此,dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1。
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (!matrix.size() || !matrix[0].size()) return 0;
int max = 0;
for (int i = 0, ie = matrix.size(); i < ie; ++i) {
for (int j = 0, je = matrix[0].size(); j < je; ++j) {
matrix[i][j] -= '0'; // convert to int
if (matrix[i][j]) {
// matrix[i][j] = min(matrix[i-1][j], matrix[i][j-1], matrix[i-1][j-1]) + 1
if (i > 0 && j > 0) {
matrix[i][j] = min(min(matrix[i-1][j-1], matrix[i-1][j]), matrix[i][j-1]) + 1;
}
if (matrix[i][j] > max) max = matrix[i][j];
}
}
}
return max * max;
}
};
85. Maximal Rectangle
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
Example:
Input: [ ["1","0","1","0","0"], ["1","0","1","1","1"], ["1","1","1","1","1"], ["1","0","0","1","0"] ] Output: 6
这道题可以用一种类似动态规划的方法来解决(或者,就是动态规划?)。使用数组height来记录每个格子向上的连续长度。对每个格子matrix[i][j],都存在一个数left[i][j],使得matrx[left[i][j] : i][j]这些格子向上的连续高度不小于height[i][j]。这些数记录在数组left中。数组right也是同理,matrx[i : right[i][j]][j]这些格子向上的连续高度不小于height[i][j]。显然,最大的那个矩形的面积,是某个格子的height[i][j] * (right[i][j] - left[i][j])。所以只要迭代地求出每个格子的height, left, right值,就可以求出最大矩形的面积。
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if (matrix.empty() || matrix[0].empty()) return 0;
int m = matrix.size(), n = matrix[0].size();
vector<int> height(n, 0), left(n, 0), right(n, n);
int tmp, max_size = 0;
for (int i = 0; i < m; ++i) {
// the index of left/right most continuous 1
int cur_left = 0, cur_right = n;
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == '0') {
// left = 0, right = n for convenience
height[j] = 0, left[j] = 0, right[j] = n;
cur_left = j + 1;
} else {
++height[j];
if (cur_left > left[j]) left[j] = cur_left;
}
}
for (int j = n - 1; j >= 0; --j) {
// compute right
if (matrix[i][j] == '0') {
cur_right = j;
} else {
if (cur_right < right[j]) right[j] = cur_right;
tmp = height[j] * (right[j] - left[j]);
if (tmp > max_size) max_size = tmp;
}
}
}
return max_size;
}
};
34. Find First and Last Position of Element in Sorted Array
Given an array of integers
numssorted in ascending order, find the starting and ending position of a giventargetvalue.Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return
[-1, -1].Example 1:
Input: nums = [5,7,7,8,8,10], target = 8 Output: [3,4]Example 2:
Input: nums = [5,7,7,8,8,10], target = 6 Output: [-1,-1]
这题可以用二分查找找到target,然后再迭代地判断nums里有多少个target。这种方法虽简单(对二分查找的写法没有要求),但却会在nums元素大部分是target时,时间复杂度上升到O(n)。一种更好的方法是用两次二分查找,分别找出第一个target和最后一个target。如何用二分查找查找一个指定的target,在我另一篇笔记里有提到。虽然在理论上保证了最差时间复杂度是O(lgn),但提交到LeetCode跑,还是没有线性查找的快,可能是数据集的原因吧……
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.empty()) return {-1, -1};
int low = 0, high = nums.size() - 1, mid;
while (low < high) {
mid = (low + high) >> 1;
if (nums[mid] < target) low = mid + 1;
else high = mid;
}
if (nums[low] != target) return {-1, -1};
int ori_low = low;
high = nums.size() - 1;
while (low < high) {
mid = ((low + high) >> 1) + 1;
if (nums[mid] > target) high = mid - 1;
else low = mid;
}
return {ori_low, high};
}
};
19. Remove Nth Node From End of List
Given a linked list, remove the n-th node from the end of list and return its head.
Example:
Given linked list: 1->2->3->4->5, and n = 2. After removing the second node from the end, the linked list becomes 1->2->3->5.
使用两个指针fast slow,先让fast走n步,然后fast和slow一起走。在fast为空时,slow到达的地方就是倒数第n个节点。注意为了删除倒数第n个节点,需要知道slow前一个节点,这可以通过:1)记录slow前一个节点;2)fast和slow少走一步两种方法来解决。下面代码是第一种方法:
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *fast = head, *slow = head, *prev = nullptr;
while (n--) fast = fast->next;
while (fast) fast = fast->next, prev = slow, slow = slow->next;
if (prev) prev->next = slow->next;
else head = head->next;
delete slow;
return head;
}
};
322. Coin Change
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return
-1.Example 1:
Input: coins = [1, 2, 5], amount = 11 Output: 3 Explanation: 11 = 5 + 5 + 1Example 2:
Input: coins = [2], amount = 3 Output: -1
这是一个完全背包问题,我之前写过一篇简单的介绍。
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
// dp[n][v] = min(dp[n-1][v], dp[n][v-coins[n]]+1)
int N = coins.size();
vector<int> dp(amount+1, 0x7ffffffe);
dp[0] = 0;
for (int n = 0; n < N; ++n) {
for (int v = coins[n]; v <= amount; ++v) {
dp[v] = min(dp[v], dp[v-coins[n]] + 1);
}
}
if (dp[amount] >= 0x7ffffffe) return -1;
return dp[amount];
}
};
138. Copy List with Random Pointer
A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.
Return a deep copy of the list.
The Linked List is represented in the input/output as a list of
nnodes. Each node is represented as a pair of[val, random_index]where:
val: an integer representingNode.valrandom_index: the index of the node (range from0ton-1) where random pointer points to, ornullif it does not point to any node.Example 1:
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]] Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]Example 2:
Input: head = [[1,1],[2,1]] Output: [[1,1],[2,1]]Example 3:
Input: head = [[3,null],[3,0],[3,null]] Output: [[3,null],[3,0],[3,null]]Example 4:
Input: head = [] Output: [] Explanation: Given linked list is empty (null pointer), so return null.
这道题在剑指offer上也有出现过。它的思路是:
-
首先,复制链表中的每一个节点(
random指针没有复制)。将链表节点的复制节点置于它下一个位置。这时链表呈以下形状:node1 -> node1_copy -> node2 -> node2_copy -> ... -> noden -> noden_copy -
重新遍历链表,修改所有复制的节点的
random指针值为正确的地址。 -
将链表间隔划分,分为原链表和复制链表,最后返回复制链表。
class Solution {
public:
Node* copyRandomList(Node* head) {
if (!head) return nullptr;
Node *curr = head;
while (curr) {
Node *add = new Node(curr->val);
add->next = curr->next, curr->next = add;
curr = curr->next->next;
}
curr = head;
while (curr) {
if (curr->random)
curr->next->random = curr->random->next;
curr = curr->next->next;
}
curr = head;
Node *vhead = new Node(0), *rtn_curr = vhead;
while (curr) {
rtn_curr->next = curr->next, rtn_curr = rtn_curr->next;
curr->next = curr->next->next, curr = curr->next;
}
rtn_curr = vhead->next;
delete vhead;
return rtn_curr;
}
};
79. Word Search
Given a 2D board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example:
board = [ ['A','B','C','E'], ['S','F','C','S'], ['A','D','E','E'] ] Given word = "ABCCED", return true. Given word = "SEE", return true. Given word = "ABCB", return false.
这题是简单的DFS。遍历board上的所有格子,如果当前格子和word首字母相同,那么便进行DFS。当前正在搜索的格子如果上下左右有其他格子和word下一个字母相同,那么就尝试对它进行更深度的搜索。在word都匹配完以后,返回true。
class Solution {
bool dfs(vector<vector<char>>& board, int i, int j, string &word, int c) {
if (c + 1 == word.length()) return true;
board[i][j] = '*';
bool flag = (i > 0 && board[i-1][j] == word[c+1] && dfs(board, i-1, j, word, c+1))
|| (j > 0 && board[i][j-1] == word[c+1] && dfs(board, i, j-1, word, c+1))
|| (i < board.size()-1 && board[i+1][j] == word[c+1] && dfs(board, i+1, j, word, c+1))
|| (j < board[0].size()-1 && board[i][j+1] == word[c+1] && dfs(board, i, j+1, word, c+1));
board[i][j] = word[c];
return flag;
}
public:
bool exist(vector<vector<char>>& board, string word) {
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
if (board[i][j] == word[0] && dfs(board, i, j, word, 0))
return true;
}
}
return false;
}
};
33. Search in Rotated Sorted Array
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e.,
[0,1,2,4,5,6,7]might become[4,5,6,7,0,1,2]).You are given a target value to search. If found in the array return its index, otherwise return
-1.You may assume no duplicate exists in the array.
Your algorithm’s runtime complexity must be in the order of O(log n).
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0 Output: 4Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3 Output: -1
首先用二分查找找出最小的元素的下标rotate,那么数组元素即向左旋转了rotate单位。有了rotate,就能从“心中的有序数组”的下标映射到实际数组的下标。比如数组[4,5,6,7,0,1,2],它在我心中应该是这样子的:[0,1,2,4,5,6,7],完美有序。已知rotate = 4,因此心中的数组下标为i的元素,在实际数组中下标应为(i + rotate) % nums.size()。我们可以对心中的数组做二分查找,但是在用nums[mid]和target比较时,就映射回实际的下标,找出它的真实值。最后我们可以找出target在心中数组的下标。将这个下标映射回实际下标即所求。二分查找的一些细节问题(比如循环判断的边界),可以参考之前我写的文章。
class Solution {
public:
int search(vector<int>& nums, int target) {
if (nums.empty()) return -1;
int low = 0, high = nums.size() - 1, mid;
while (low < high) {
mid = (low + high) >> 1;
if (nums[mid] > nums[high]) low = mid + 1;
else high = mid;
}
int rotate = low, real_mid;
low = 0, high = nums.size() - 1;
while (low <= high) {
mid = (low + high) >> 1;
real_mid = (mid + rotate) % nums.size();
if (nums[real_mid] == target) return real_mid;
else if (nums[real_mid] < target) low = mid + 1;
else high = mid - 1;
}
return -1;
}
};
这个方法用了两次二分查找,这位大神的方法明显更加优越,只用了一次二分查找(StefanPochmann大神总是这么秀……)首先,我们可以把旋转后的数组看做两边,左边的数比右边的大。一个数落在哪一边可以通过和nums[0]或者nums.back()比较得知。假如target落在了左边,那么我们把右边的数全部设为INF,这样数组便有序了,直接对这个修改后的数组做一次二分查找即可找出target的下标。反之,如果target落在右边,我们就把左边的数全部设为-INF,令数组有序,并且可以通过一次二分查找找到target。我们不必真的去修改数组,只需要在二分查找的过程中,对nums[mid]和target是否在同一边进行判断。如果它们在同一边,保留nums[mid];否则将nums[mid]设为INF或者-INF。
class Solution {
public:
int search(vector<int>& nums, int target) {
if (nums.empty()) return -1;
int low = 0, high = nums.size() - 1, mid, num;
while (low <= high) {
mid = (low + high) >> 1;
if ((nums[mid] < nums[0]) == (target < nums[0])) num = nums[mid];
else if (target < nums[0]) num = 0x80000000;
else num = 0x7fffffff;
if (num == target) return mid;
else if (num < target) low = mid + 1;
else high = mid - 1;
}
return -1;
}
};
55.45.1306. Jump Game & II & III
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
Example 1:
Input: nums = [2,3,1,1,4] Output: true Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.Example 2:
Input: nums = [3,2,1,0,4] Output: false Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
用一个变量max_len记录当前能到达的最远距离,另一个变量position记录当前所在位置。如果position + nums[position] > max_len,说明现在能跳到更远的地方,则更新max_len。如果max_len >= nums.size() - 1,说明能够跳到最后一个元素,因此返回true。
class Solution {
public:
bool canJump(vector<int>& nums) {
if (nums.empty() || nums.size() == 1) return true;
int max_len = 0, position = 0;
while (position <= max_len) {
if (nums[position] + position > max_len) {
max_len = nums[position] + position;
if (max_len >= nums.size() - 1) return true;
}
++position;
}
return false;
}
};
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
Example:
Input: [2,3,1,1,4] Output: 2 Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
这其实可以看做是一个BFS问题。求出走n步,可以到达的元素;根据这些元素,找出走n+1步可以到达的元素。假如走了x步,我们发现可以到达nums[-1]了,就认为最少跳数为x。这种做法虽简单,但每走一步要记录所有可以到达的元素,开销实在太大。更好的方法是记录走n步可以到达的最远的元素。这个最远元素左边的元素,到达步数不大于n步。假设走n-1步最远可以到达的元素是nums[j],走n步最远可以到达的元素是nums[k],那么显然,走到nums[j]和nums[k]之间的元素所需步数至少是n。因此,我们在BFS过程中,记录走n步可以到达的最远元素,然后和走n-1步可以到达的最远元素比较,就可以知道它们之间元素的最短跳数了。
class Solution {
public:
int jump(vector<int>& nums) {
if (nums.empty() || nums.size() == 1) return 0;
int cur_max = 0, jump = 0, i = 0, next_max, n = nums.size();
while (cur_max < n - 1) {
next_max = cur_max, ++jump;
for ( ; i <= cur_max; ++i) {
next_max = max(next_max, i + nums[i]);
}
cur_max = next_max;
}
return jump;
}
};
Given an array of non-negative integers
arr, you are initially positioned atstartindex of the array. When you are at indexi, you can jump toi + arr[i]ori - arr[i], check if you can reach to any index with value 0.Notice that you can not jump outside of the array at any time.
Example 1:
Input: arr = [4,2,3,0,3,1,2], start = 5 Output: true Explanation: All possible ways to reach at index 3 with value 0 are: index 5 -> index 4 -> index 1 -> index 3 index 5 -> index 6 -> index 4 -> index 1 -> index 3Example 2:
Input: arr = [4,2,3,0,3,1,2], start = 0 Output: true Explanation: One possible way to reach at index 3 with value 0 is: index 0 -> index 4 -> index 1 -> index 3Example 3:
Input: arr = [3,0,2,1,2], start = 2 Output: false Explanation: There is no way to reach at index 1 with value 0.
这题是一个DFS题。从start出发,使用DFS搜索,看是否能够到达一个值为0的元素。对于一个已访问过的元素,将其值取反以表示访问过。
class Solution {
public:
bool canReach(vector<int>& arr, int start) {
queue<int> q;
q.push(start);
int curr, n = arr.size(), count = 0, left, right;
while (!q.empty()) {
curr = q.front(), q.pop();
if ((left=curr-arr[curr]) >= 0) {
if (arr[left] == 0) return true;
else if (arr[left] > 0)
q.push(left);
}
if ((right=curr+arr[curr]) < n) {
if (arr[right] == 0) return true;
else if (arr[right] > 0)
q.push(right);
}
arr[curr] = -arr[curr];
}
return false;
}
};
84. Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Above is a histogram where width of each bar is 1, given height =
[2,1,5,6,2,3].
The largest rectangle is shown in the shaded area, which has area =
10unit.Example:
Input: [2,1,5,6,2,3] Output: 10
这道题和LeetCode 85很像。对于每个bar,寻找它左边第一个比它小的bar1,和它右边第一个比它小的bar2。计算由bar1和bar2所夹的矩形的面积值size(以当前bar的高度为高)。显然,最大的矩形面积值一定出自于某个bar的size。在寻找bar1和bar2的时候,可以借助一个栈。栈中元素从底到顶按从小到大排列。以寻找bar1为例,我们希望栈顶存储的是当前bar左边第一个比它小的bar1。每当当前bar的高度小于栈顶元素时,我们就pop栈,这是因为栈顶元素不可能是当前bar右边的bar的“左边第一个比它小的bar”。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
if (heights.empty()) return 0;
vector<int> left(heights.size());
int right, max_h = -1;
stack<int> st;
for (int i = 0; i < heights.size(); ++i) {
while(!st.empty() && heights[st.top()] >= heights[i]) st.pop();
if (st.empty()) left[i] = -1;
else left[i] = st.top();
st.push(i);
}
st = stack<int>();
for (int i = heights.size() - 1; i >= 0; --i) {
while (!st.empty() && heights[st.top()] >= heights[i]) st.pop();
if (st.empty()) right = heights.size();
else right = st.top();
max_h = max(max_h, (right - left[i] - 1) * heights[i]);
st.push(i);
}
return max_h;
}
};
76.3 Minimum Window Substring & Longest Substring Without Repeating Characters
Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).
Example:
Input: S = "ADOBECODEBANC", T = "ABC" Output: "BANC"
这题在评论区有一个非常好的总结。我们使用一个数组map来记录每个字符的情况。其中,map[c] > 0代表字符c存在于t中,且窗口中还欠缺map[c]个c;map[c] == 0代表字符c不存在t中,或者存在于t中且已经被包含在窗口中,都说明窗口不需要将c包括进来;map[c] < 0代表字符c不存在t中。我们还使用变量begin end来标记窗口的起始结束位置,用counter来记录窗口还欠缺的字符数量。
一开始对于t中所有的字符c,令map[c]++。然后遍历s,每遇到一个字符c,就将它收纳进窗口中。如果map[c] > 0,说明碰到了一个可以被收纳进窗口的字符,就令counter--。我们令map[c]--,以表示c已经被收纳进窗口。后面会提到,我们会令map[c]++来表示c被移出窗口。
当counter == 0时,当前窗口包含了t中所有的字符。当前窗口的大小是end - begin + 1。如果当前窗口的大小小于历史窗口大小的最小值,那就更新最小值。然后,我们需要将begin向前移,即将窗口向前移。如前所说,每将一个字符移出窗口后,就令它的map[c]++。在移出一个c以后,如果它的map[c]变为1,说明我们移出了一个包含于t中的字符,且窗口不再包含t中所有字符了。这时我们就不能继续前移窗口了,而是应该重复之前的过程,直到我们再次令窗口包含所有t中字符为止。
class Solution {
public:
string minWindow(string s, string t) {
vector<int> map(128, 0);
for (char c: t) ++map[c];
int begin = 0, counter = t.length();
int min_len = 0x7fffffff, min_begin = -1; // begin of the min window
for (int end = 0; end < s.length(); ++end) {
if (map[s[end]]-- > 0) --counter;
while (!counter) {
if (end - begin + 1 < min_len)
min_len = end - begin + 1, min_begin = begin;
if (map[s[begin++]]++ == 0) ++counter;
}
}
if (min_begin == -1) return "";
return s.substr(min_begin, min_len);
}
};
Given a string, find the length of the longest substring without repeating characters.
Example 1:
Input: "abcabcbb" Output: 3 Explanation: The answer is "abc", with the length of 3.Example 2:
Input: "bbbbb" Output: 1 Explanation: The answer is "b", with the length of 1.Example 3:
Input: "pwwkew" Output: 3 Explanation: The answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.
运用上面链接所介绍的思想,这道题也可以用滑动窗口来做。用一个数组map记录所有字符的状态。每当一个字符c进入窗口,就令map[c]--;出窗口时map[c]++。当有一个map[c] == -2时,说明窗口内字符出现了重复,需要向前移动窗口,直到窗口内没有重复字符为止。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
vector<int> map(128, 0);
int begin = 0, max_len = 0;
for (int end = 0; end < s.length(); ++end) {
if (--map[s[end]] == -2) { // duplicate char
while (++map[s[begin++]] != -1) ;
}
if (max_len < end - begin + 1)
max_len = end - begin + 1;
}
return max_len;
}
};
124. Binary Tree Maximum Path Sum
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3] 1 / \ 2 3 Output: 6Example 2:
Input: [-10,9,20,null,null,15,7] -10 / \ 9 20 / \ 15 7 Output: 42
这题我的做法和评论区的如出一辙,可能是我最接近大神们的一次了,嘤嘤嘤……对每个节点,我们求以它为起始点,向下走,能达到的最大路径maxSinglePath。另一方面,题目规定的路径是可以从一个稍低的节点出发,走到更高的节点的。假如以节点n为最高节点的路径为p,显然p的最大值为它左孩子的maxSinglePath(如果大于0)加上它右孩子的maxSinglePath(如果大于0)加上n->val。所以,我们可以一边递归地求所有节点的maxSinglePath,顺便计算p的最大值。
class Solution {
int max_path;
int maxSinglePath(TreeNode *node) {
if (!node) return 0;
int left = maxSinglePath(node->left);
int right = maxSinglePath(node->right);
// discard negative paths
if (left < 0) left = 0;
if (right < 0) right = 0;
if (left + right + node->val > max_path)
max_path = left + right + node->val;
return node->val + (left > right ? left : right);
}
public:
int maxPathSum(TreeNode* root) {
if (!root) return 0;
max_path = 0x80000000;
maxSinglePath(root);
return max_path;
}
};
2.445. Add Two Numbers & II
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example:
Input: (2 -> 4 -> 3) + (5 -> 6 -> 4) Output: 7 -> 0 -> 8 Explanation: 342 + 465 = 807.
同时遍历l1和l2,并加节点值相加,记录进位carry。我的写法有点啰嗦,三个循环体的代码基本相同,这个人写的会简洁一点。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode *vhead = new ListNode(0), *curr = vhead;
int carry = 0;
while (l1 && l2) {
curr->next = new ListNode(l1->val + l2->val + carry);
curr = curr->next, l1 = l1->next, l2 = l2->next;
carry = curr->val / 10, curr->val %= 10;
}
while (l1) {
curr->next = new ListNode(l1->val + carry);
curr = curr->next, l1 = l1->next;
carry = curr->val / 10, curr->val %= 10;
}
while (l2) {
curr->next = new ListNode(l2->val + carry);
curr = curr->next, l2 = l2->next;
carry = curr->val / 10, curr->val %= 10;
}
if (carry) curr->next = new ListNode(1);
curr = vhead->next;
delete vhead;
return curr;
}
};
The most significant digit comes first and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.
Example:
Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4) Output: 7 -> 8 -> 0 -> 7
使用两个栈来记录两个的翻转。像上面那样求两个链表的和,注意构造结果链表时也是要反向构造的。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
stack<int> st1, st2;
while (l1) st1.push(l1->val), l1 = l1->next;
while (l2) st2.push(l2->val), l2 = l2->next;
int carry = 0, sum;
ListNode *rtn = nullptr;
while (!st1.empty() || !st2.empty() || carry) {
sum = carry;
if (!st1.empty()) sum += st1.top(), st1.pop();
if (!st2.empty()) sum += st2.top(), st2.pop();
ListNode *head = new ListNode(sum % 10);
head->next = rtn, rtn = head;
carry = sum / 10;
}
return rtn;
}
};
146. LRU Cache
Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations:
getandput.
get(key)- Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.put(key, value)- Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.The cache is initialized with a positive capacity.
Follow up: Could you do both operations in O(1) time complexity?
Example:
LRUCache cache = new LRUCache( 2 /* capacity */ ); cache.put(1, 1); cache.put(2, 2); cache.get(1); // returns 1 cache.put(3, 3); // evicts key 2 cache.get(2); // returns -1 (not found) cache.put(4, 4); // evicts key 1 cache.get(1); // returns -1 (not found) cache.get(3); // returns 3 cache.get(4); // returns 4
使用一个双向链表来记录不同键上一次被访问时间的次序。处于链表头部的键越晚被访问,因此越难被移出缓存中。用另一个哈希表,将键映射到值和它在双向链表中的位置。当我们访问/更新一个已有键,需要更改它的LRU优先级时,可以通过哈希表在O(1)时间内获取它在链表中的位置,将其移除,再添加到链表头部即可。如果缓存存满,需要移除一个victim,直接将链表优先级最低的元素,即尾部元素移除即可。
class LRUCache {
int capacity;
list<int> LRUOrder;
typedef list<int>::iterator lit;
unordered_map<int, pair<int, lit>> key2valueNorder;
typedef unordered_map<int, pair<int, lit>>::iterator uit;
public:
LRUCache(int capacity) : capacity(capacity) {}
int get(int key) {
uit it = key2valueNorder.find(key);
if (it == key2valueNorder.end()) return -1;
updateOrder(it);
return it->second.first;
}
void put(int key, int value) {
uit it = key2valueNorder.find(key);
if (it == key2valueNorder.end()) {
if (key2valueNorder.size() >= capacity) {
// remove victim
key2valueNorder.erase(LRUOrder.back());
LRUOrder.pop_back();
}
LRUOrder.push_front(key);
key2valueNorder[key] = {value, LRUOrder.begin()};
} else {
// update value and order
it->second.first = value;
updateOrder(it);
}
}
void updateOrder(uit it) {
LRUOrder.erase(it->second.second);
LRUOrder.push_front(it->first);
it->second.second = LRUOrder.begin();
}
};
41. First Missing Positive
Given an unsorted integer array, find the smallest missing positive integer.
Example 1:
Input: [1,2,0] Output: 3Example 2:
Input: [3,4,-1,1] Output: 2Example 3:
Input: [7,8,9,11,12] Output: 1
我的想法是在原数组上记录有哪些正数存在。比如在遍历过程中,我发现了一个1,那么我就将nums[1-1]设为0x80000001,表示1存在于数组中。如果nums[1-1]原本就是一个正数,为了不覆盖这个正数,要先将nums[nums[1-1]-1]设为0x80000001。注意nums[nums[1-1]-1]也可能是一个正数,我们需要递归地先将可能被覆盖的正数记录下来,直到遇到一个非正数为止(非正数没有用)。这个方法虽然通过了测试样例,但似乎很耗时,在评论区有更好的记录已存在正数的,比如:
- 第一种,将符合范围(
[1, nums.size()])的元素移动到相应的位置上。 - 第二种,
nums[nums[i]%n] += n。只要有nums[i] < n,说明i这个数没被+=n过,因此不存在于数组中。
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
for (int i = 0, j, k; i < nums.size(); ++i) {
if (nums[i] != 0x80000001 && nums[i] > 0) {
// current position and next position
j = i, k = nums[j] - 1;
while (j >= 0 && k >= 0 && k < nums.size()) {
j = k, k = nums[k] - 1;
nums[j] = 0x80000001;
}
}
}
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != 0x80000001)
return i + 1;
}
return nums.size() + 1;
}
};
152. Maximum Product Subarray
Given an integer array
nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.Example 1:
Input: [2,3,-2,4] Output: 6 Explanation: [2,3] has the largest product 6.Example 2:
Input: [-2,0,-1] Output: 0 Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
使用两个变量i_max i_min来记录以当前元素nums[i]结尾的子数组连乘能够得到的最大值和最小值。显然,如果nums[i+1] < 0,那么对应的i_max = max(nums[i+1], i_min * nums[i+1]),因为一个更小的数乘负数结果会更大。反之同理,i_min = max(nums[i+1], i_max * nums[i+1])。对于所有的nums[i],都求一次i_max,即可知道全局的maxProduct是多少。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int rtn = nums[0];
int i_max = rtn, i_min = rtn;
for (int i = 1; i < nums.size(); ++i) {
if (nums[i] < 0) swap(i_max, i_min);
i_max = max(nums[i], i_max * nums[i]), i_min = min(nums[i], i_min * nums[i]);
if (i_max > rtn) rtn = i_max;
}
return rtn;
}
};
581. Shortest Unsorted Continuous Subarray
Given an integer array, you need to find one continuous subarray that if you only sort this subarray in ascending order, then the whole array will be sorted in ascending order, too.
You need to find the shortest such subarray and output its length.
Example 1:
Input: [2, 6, 4, 8, 10, 9, 15] Output: 5 Explanation: You need to sort [6, 4, 8, 10, 9] in ascending order to make the whole array sorted in ascending order.
所谓的unsorted continuous array,一定是起始于数组中第一个 大于某个之后元素 的元素,结束于最后一个 小于某个之前元素 的元素。unsorted array包含了所有需要调整位置的元素,并且要最短,所以它的首尾一定是乱序元素。为了找出这两个首尾元素,我们可以记录当前元素之后元素的最小值,以及当前元素之前元素的最大值。如果当前元素大于之后元素的最大值,说明是乱序的;小于之前元素的最大值说明也是乱序的。
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
int back_min = 0x7fffffff, head = -1;
for (int i = nums.size()-1; i >= 0; --i) {
if (nums[i] <= back_min) back_min = nums[i];
else head = i;
}
if (head == -1) return 0;
int front_max = 0x80000000, tail;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] >= front_max) front_max = nums[i];
else tail = i;
}
return tail - head + 1;
}
};
// 或者只用一趟遍历
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
int back_min = 0x7fffffff, head = -1, front_max = 0x80000000, tail = -2;
int reverse_idx;
for (int i = 0, n = nums.size(); i < n; ++i) {
reverse_idx = n - i - 1;
if (nums[reverse_idx] <= back_min) back_min = nums[reverse_idx];
else head = reverse_idx;
if (nums[i] >= front_max) front_max = nums[i];
else tail = i;
}
return tail - head + 1;
}
};
5. Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: "babad" Output: "bab" Note: "aba" is also a valid answer.Example 2:
Input: "cbbd" Output: "bb"
回文串有两种,一种是奇数个字符的,一种是偶数个字符的。对于s中的每个字符c,我们需要考虑两种情况:
- 以
c为中心的奇数个字符的回文串。 - 以
c和c下一个字符为中心的偶数个字符的回文串。
在我们知道s[i:j]是一个回文串以后,如果s[i-1] == s[j],说明s[i-1:j+1]也是一个回文串。
class Solution {
public:
string longestPalindrome(string s) {
if (!s.length()) return "";
int max_len = 0, max_idx;
for (int i = 0, n = s.length(), left, right; i < n; ++i) {
// s[i] as middle
left = i - 1, right = i + 1;
while (left >= 0 && right < n && s[left] == s[right]) --left, ++right;
if (right - left - 1 > max_len) max_len = right - left - 1, max_idx = left + 1;
// s[i] ans s[i+1] as middle
left = i, right = i + 1;
while (left >= 0 && right < n && s[left] == s[right]) --left, ++right;
if (right - left - 1 > max_len) max_len = right - left - 1, max_idx = left + 1;
}
return s.substr(max_idx, max_len);
}
};
4. Median of Two Sorted Arrays
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
You may assume nums1 and nums2 cannot be both empty.
Example 1:
nums1 = [1, 3] nums2 = [2] The median is 2.0Example 2:
nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
这题对我挺难的,我直接看了这个答案。
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
if (m > n) nums1.swap(nums2), m = nums1.size(), n = nums2.size();
int imin = 0, imax = m, half_len = (m + n + 1) / 2, i, j;
while (imin <= imax) {
i = (imin + imax) / 2, j = half_len - i;
if (i < m && nums2[j-1] > nums1[i]) imin = i + 1;
else if (i > 0 && nums1[i-1] > nums2[j]) imax = i - 1;
else {
int max_of_left, min_of_right;
if (i == 0) max_of_left = nums2[j-1];
else if (j == 0) max_of_left = nums1[i-1];
else max_of_left = max(nums1[i-1], nums2[j-1]);
if ((m + n) % 2 == 1) return max_of_left;
if (i == m) min_of_right = nums2[j];
else if (j == n) min_of_right = nums1[i];
else min_of_right = min(nums1[i], nums2[j]);
return (max_of_left + min_of_right) / 2.0;
}
}
return -1; // never reach here
}
};
32. Longest Valid Parentheses
Given a string containing just the characters
'('and')', find the length of the longest valid (well-formed) parentheses substring.Example 1:
Input: "(()" Output: 2 Explanation: The longest valid parentheses substring is "()"Example 2:
Input: ")()())" Output: 4 Explanation: The longest valid parentheses substring is "()()"
我们使用一个栈来存储尚未匹配的左括号的下标。每遇到一个左括号,就将它的下标压入栈。如果遇到一个右括号,就弹出一个下标,表示弹出的左括号和这个右括号相匹配。这样的话,当前匹配的字符串长度就是i - stack[-1]。由于可能会出现右括号多于左括号的情况,我们可以在栈中预留一个类似“底部”的下标。str[:bottom+1]这些括号可以被认为是无用的,之后的括号不可能和它们匹配。一开始这个bottom = -1,当我们遇到一个右括号并从栈中弹出一个元素后,如果栈为空,说明我们触及底部了,也意味着当前右括号数量比左括号数量更多,这种情况下str[:i+1]是不可能和之后的括号匹配的。因此我们将i压入栈中,作为新的底部。底部这个设计很巧妙,简化了很多代码。
class Solution {
public:
int longestValidParentheses(string s) {
stack<int> st;
st.push(-1);
int max_len = 0;
for (int i = 0; i < s.length(); ++i) {
if (s[i] == '(') st.push(i);
else {
st.pop();
if (st.empty()) st.push(i);
else max_len = max(max_len, i - st.top());
}
}
return max_len;
}
};
98. Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
2 / \ 1 3 Input: [2,1,3] Output: trueExample 2:
5 / \ 1 4 / \ 3 6 Input: [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.
一棵二叉搜索树被中序遍历,产生的序列一定是有序的。因此,我们对这个二叉树做中序遍历。如果遍历序列是失序的,说明不是二叉搜索树。
class Solution {
public:
bool isValidBST(TreeNode* root) {
// inorder
stack<TreeNode*> st;
TreeNode *curr = root, *prev = nullptr;
while (curr) {
while (curr) st.push(curr), curr = curr->left;
do {
curr = st.top(), st.pop();
// visit curr
if (prev && curr->val <= prev->val) return false;
prev = curr;
} while (!curr->right && !st.empty());
curr = curr->right;
}
return true;
}
};
10. Regular Expression Matching
Given an input string (
s) and a pattern (p), implement regular expression matching with support for'.'and'*'.'.' Matches any single character. '*' Matches zero or more of the preceding element.The matching should cover the entire input string (not partial).
Note:
scould be empty and contains only lowercase lettersa-z.pcould be empty and contains only lowercase lettersa-z, and characters like.or*.Example 1:
Input: s = "aa" p = "a" Output: false Explanation: "a" does not match the entire string "aa".Example 2:
Input: s = "aa" p = "a*" Output: true Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".Example 3:
Input: s = "ab" p = ".*" Output: true Explanation: ".*" means "zero or more (*) of any character (.)".Example 4:
Input: s = "aab" p = "c*a*b" Output: true Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore, it matches "aab".Example 5:
Input: s = "mississippi" p = "mis*is*p*." Output: false
这道题有两种做法。第一种是状态机。我之前写过一个状态机的回答,复制在这里:
下面图是p = "a*b"时两种状态机(NFA和DFA)的示意图。
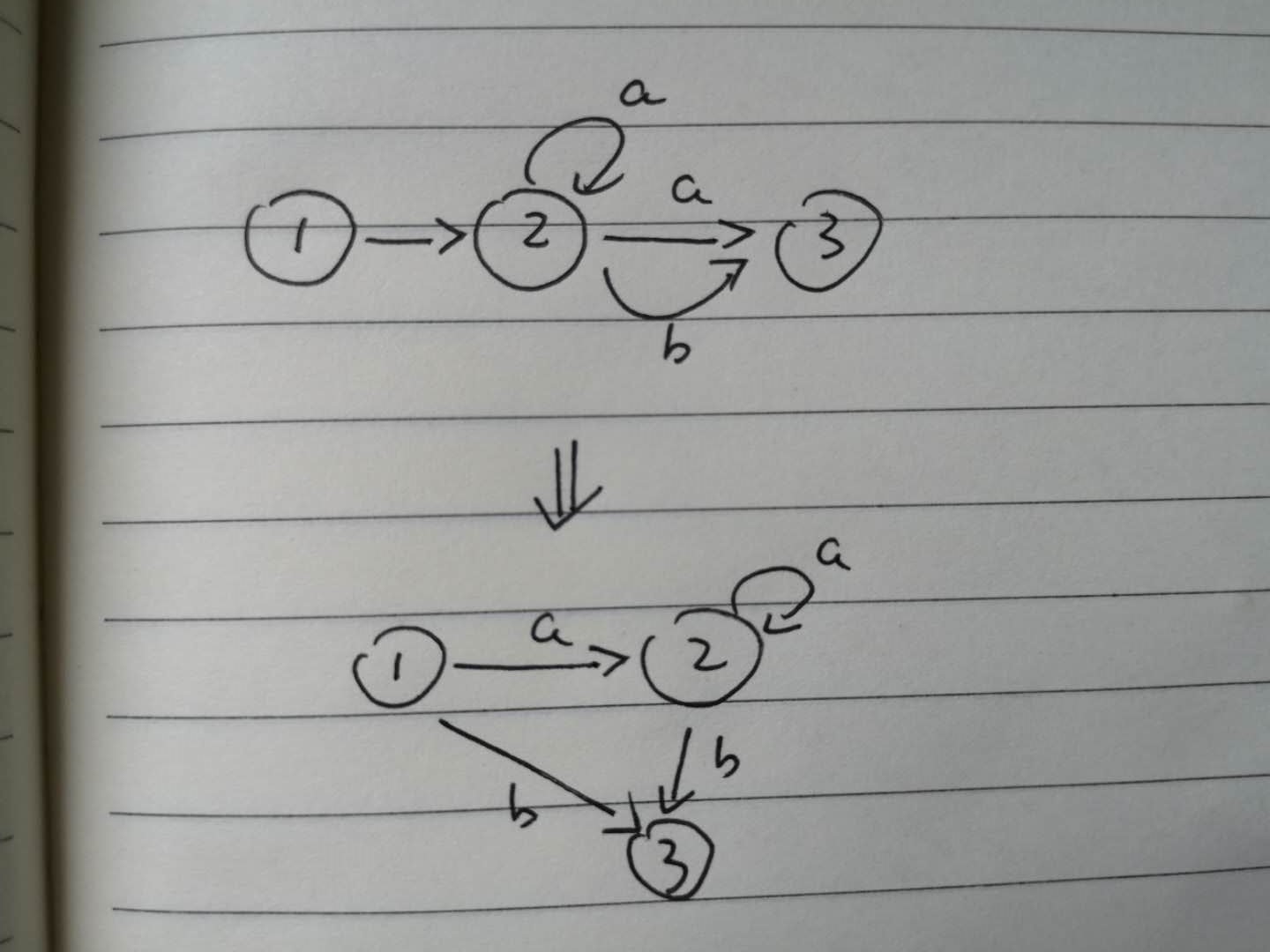
This version of my state machine is easy to understand. However, this is a NFA (Nondeterminism Finite Automaton). Without further optimization, my code got Time Limit Exceeded when submitted to LeetCode. A good solution is to transform it to a DFA (Deterministic Finite Automation).
Here is a DFA written by cbmbbz:
# NFA
class Solution:
def isMatch(self, s: str, p: str) -> bool:
state_machine = self.build_machine(p)
# search the state machine with s, if s is possible to reach the end state,
# p matches s
return self.search_machine(state_machine, s)
@staticmethod
def build_machine(pattern):
head = State(0) # entry
current_state = head
i = 0
while i < len(pattern):
# check whether there is a * after the current letter
if i < len(pattern) - 1 and pattern[i+1] == '*':
# it is a loop state
current_state = current_state.set_next(2, pattern[i])
i += 1 # skip '*'
else:
current_state = current_state.set_next(1, pattern[i])
i += 1
# end state
current_state.set_next(3)
return head
def search_machine(self, current_state, s):
# move among states according to characters of s
if current_state.type == 3:
# end state, if len(s) != 0, it means that some characters of s could not be matched by p
if len(s) > 0:
return False
return True
# all possible states to go next & substrings of s passed to next state
possible_next = []
if current_state.type == 0:
# start state, keep s and go to the next state
possible_next.append((current_state.next, s))
elif current_state.type == 1:
if len(s) == 0:
# no characters to match
return False
# a normal state. if the letter of the state is equal to s[0], just go to the next state with
# the rest characters of s
if s[0] == current_state.letter or current_state.letter == '.':
possible_next.append((current_state.next, s[1:]))
else:
return False
else:
if len(s) == 0:
# no characters to match. have to go to next state
possible_next.append((current_state.next, s))
# a loop state. maybe this state takes away 0 character from s.
elif s[0] == current_state.letter or current_state.letter == '.':
# take 0 character and go to next state
possible_next.append((current_state.next, s))
# take 1 character and loop in this state
possible_next.append((current_state, s[1:]))
# take 1 character and go to next state
possible_next.append((current_state.next, s[1:]))
else:
# s[0] does not match the letter of current state. have to go to next state
possible_next.append((current_state.next, s))
# go to next state
for next_state, next_s in possible_next:
if self.search_machine(next_state, next_s):
# it is possible to reach the end state
return True
return False
class State:
def __init__(self, type=0, letter='.'):
"""
:param type:
0: start
1: normal
2: loop
3: end
:param letter: if type = 1 or 2, the State object will have a letter
"""
self.type = type
self.next = None
self.letter = letter
def set_next(self, type=0, letter='.'):
self.next = State(type, letter)
return self.next
# DFA
from collections import defaultdict
class Solution:
def isMatch(self, s, p):
transfer = defaultdict(set)
curr_states = [0]
for i,c in enumerate(p):
if c=='*':
continue
# an id for new state
new_state = curr_states[-1] + 1
for state in curr_states:
transfer[state, c].add(new_state)
if i < len(p) - 1 and p[i + 1] == '*': # if next c is *
transfer[new_state, c] = {new_state}
curr_states.append(new_state)
else:
curr_states = [new_state]
success = curr_states # final states
curr_states = {0}
for c in s:
next_states = set()
for state in curr_states:
next_states.update(transfer[state, c] | transfer[state, '.'])
curr_states = next_states
return any(state in curr_states for state in success) # check any curr_states is success
动态规划的做法更为直观。设dp[i][j]为s[:i]和p[:j]是否匹配。如果匹配dp[i][j]则为True,否则为False。如果s[i] == p[j],那么一定是因为p[j]是一个字母,刚好与s[i]相同。这种情况下,如果s[:i]和p[:j]匹配上,那么s[:i+1]和p[:j+1]就能匹配上。即:
dp[i+1][j+1] = dp[i][j]。
如果s[i] != p[j],那么就要看p[j]是什么了。如果p[j]是一个字母,那么s[i]和p[j]就不可能匹配上了(因为结尾部分不一样)。因此,dp[i+1][j+1] = False。如果p[j]不是字母,而是通配符.,那么不管s[i]是什么都能匹配上,因此dp[i+1][j+1] = dp[i][j],只需要s[:i]和p[:j]匹配上就可以了。如果p[j]是*,那么有三种情况:
x*(x是p[j-1])不和s[:i+1]中的字母匹配。那么s[:i+1]和p[:j+1]要匹配上,必须要让s[:i+1]和p[:j-1]匹配上,因此dp[i+1][j+1] = dp[i+1][j-1]。x*和s[i]匹配,即只匹配一个字母。这种情况的前提是x == s[i]。满足前提后,如果s[:i]能和p[:j-1]匹配上的话,s[:i+1]和p[:j+1]就能匹配上。因此,dp[i+1][j+1] = dp[i][j-1]。x*和若干个s中的字母匹配。在这种情况下,如果s[:i+1]和p[:j+1]匹配上了,肯定有s[:i]也和p[:j+1]能匹配上,因为x*能和s尾部若干个(大于1个)字母匹配。因此,dp[i+1][j+1] = dp[i][j+1]。
综上,代码如下:
class Solution {
public:
bool isMatch(string str, string pattern) {
int len_s = 0, len_p = 0;
for (; str[len_s] != '\0'; ++len_s) ;
for (; pattern[len_p] != '\0'; ++len_p) ;
int dp[len_s+1][len_p+1];
for (int i = 0; i <= len_s; ++i)
for (int j = 0; j <= len_p; ++j)
dp[i][j] = 0;
dp[0][0] = 1;
for (int j = 1; j < len_p; j+=2) {
if (pattern[j] == '*') dp[0][j+1] = 1;
else break;
}
for (int i = 0; i < len_s; ++i) {
for (int j = 0; j < len_p; ++j) {
if (str[i] == pattern[j] || pattern[j] == '.')
dp[i+1][j+1] = dp[i][j];
else if (pattern[j] == '*') {
if (j > 0) {
dp[i+1][j+1] |= dp[i+1][j-1];
if (pattern[j-1] == str[i] || pattern[j-1] == '.') {
dp[i+1][j+1] |= dp[i][j-1];
dp[i+1][j+1] |= dp[i][j+1];
}
}
}
}
}
return dp[len_s][len_p];
}
};